Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Navitgation) Markierung: Quelltext-Bearbeitung 2017 |
K (Video ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 13: | Zeile 13: | ||
Leite mithilfe des nachfolgenden GeoGebra-Applets die Formel für den Flächeninhalt eines Drachens (Deltoid) her: | Leite mithilfe des nachfolgenden GeoGebra-Applets die Formel für den Flächeninhalt eines Drachens (Deltoid) her: | ||
<ggb_applet id="XegTG3f9" width="1280" height="604" border="888888" /> | <ggb_applet id="XegTG3f9" width="1280" height="604" border="888888" /> | ||
<br><br> | |||
{{#ev:youtube|JxoPxxspgU4|800|center}}<br><br> | |||
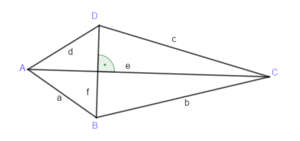
{{Box|1=Flächeninhalt und Umfang eines Drachen (Deltiod)|2=[[Datei:Drachen Bild.png|rahmenlos|rechts]] | {{Box|1=Flächeninhalt und Umfang eines Drachen (Deltiod)|2=[[Datei:Drachen Bild.png|rahmenlos|rechts]] | ||
<br /><br> | <br /><br> | ||
Version vom 30. Dezember 2020, 07:11 Uhr
4.4) Drachenviereck: Umfang und Flächeninhalt (Sprinteraufgabe)
Leite mithilfe des nachfolgenden GeoGebra-Applets die Formel für den Flächeninhalt eines Drachens (Deltoid) her:

Um die Tabelle auszufüllen, musst du die Flächeninhaltsformel umstellen:
A = |∙2
2∙A = e∙f |:e
= f | gegebene Werte einsetzen
= f | berechne, denke ans Kürzen
Stelle die Formel nach e um:
A = |∙2
2∙A = e∙f |:f
= e | gegebene Werte einsetzen
= e | berechne, denke ans Kürzen
Achte auf gleiche Einheiten! e=380cm = 3,8m
Löse dann wie in Aufgabenteil a)
Löse dann wie in Aufgabenteil a)
Achte auf gleiche Einheiten! f = 14,5dm = 1,45m
Alternativ kannst du auch die Fläche in dm² angeben:
0,9425m² = 94,25dm² (Verwandlungszahl 100!)Löse dann wie in Aufgabenteil 2)
Alternativ kannst du auch die Fläche in dm² angeben:
0,9425m² = 94,25dm² (Verwandlungszahl 100!)Löse dann wie in Aufgabenteil 2)