Benutzer:Buss-Haskert/Vierecke und Dreiecke/Zusammengesetzte Figuren: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Tipp ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
{{Navigation | [[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | ||
{{Navigation|[[Benutzer:Buss-Haskert/Vierecke und Dreiecke| Einstieg und Vorwissen]]<br>[[Buss-Haskert/Vierecke und Dreiecke/Vierecke und ihre Eigenschaften|1) Vierecke und ihre Eigenschaften <br> 2) Haus der Vierecke]]<br>[[Buss-Haskert/Vierecke und Dreiecke/Winkelsumme|3) Winkelsumme im Viereck]]<br>[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt|4) Umfang und Flächeninhalt]]<br> | |||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt|4.1) Quadrat und Rechteck]]<br> | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt|4.1) Quadrat und Rechteck]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Parallelogramm|4.2) Parallelogramm]]<br> | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Parallelogramm|4.2) Parallelogramm]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/ | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Dreieck|4.3) Dreieck]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/ | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Trapez|4.4) Trapez]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen|4. | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen|4.5) Drachen]] | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Zusammengesetzte Figuren|4. | *[[Buss-Haskert/Vierecke und Dreiecke/Zusammengesetzte Figuren|4.6) Zusammengesetzte Figuren]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Bunte Mischung|4. | *[[Buss-Haskert/Vierecke und Dreiecke/Bunte Mischung|4.7) Bunte Mischung]]<br> | ||
[[Buss-Haskert/Vierecke und Dreiecke/Checkliste|5) Checkliste]]}} | [[Buss-Haskert/Vierecke und Dreiecke/Checkliste|5) Checkliste]]}} | ||
===4.5) Zusammengesetzte Figuren=== | ===4.5) Zusammengesetzte Figuren=== | ||
| Zeile 27: | Zeile 28: | ||
Berechne dann die Flächeninhalte der Teilflächen und anschließend den Flächeninhalt der Figur. Achte auf eine übersichtliche Darstellung. | Berechne dann die Flächeninhalte der Teilflächen und anschließend den Flächeninhalt der Figur. Achte auf eine übersichtliche Darstellung. | ||
* S. 94 Nr. 1 | * S. 94 Nr. 1 | ||
* S. 94 Nr. | * S. 94 Nr. 2b | ||
* S. 94 Nr. 3|Üben}} | * S. 94 Nr. 3|Üben}} | ||
<div class="grid"> | <div class="grid"> | ||
Aktuelle Version vom 20. November 2024, 16:13 Uhr
Einstieg und Vorwissen
1) Vierecke und ihre Eigenschaften
2) Haus der Vierecke
3) Winkelsumme im Viereck
4) Umfang und Flächeninhalt
1) Vierecke und ihre Eigenschaften
2) Haus der Vierecke
3) Winkelsumme im Viereck
4) Umfang und Flächeninhalt
- 4.1) Quadrat und Rechteck
- 4.2) Parallelogramm
- 4.3) Dreieck
- 4.4) Trapez
- 4.5) Drachen
- 4.6) Zusammengesetzte Figuren
- 4.7) Bunte Mischung
4.5) Zusammengesetzte Figuren
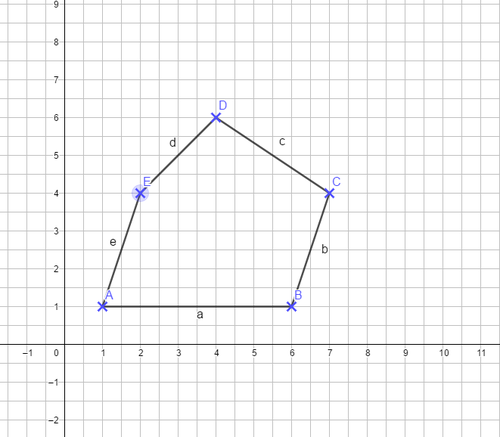
Zerlege die Figur:
1a) in Rechtecke [Verwende die Methode Ergänzen.]
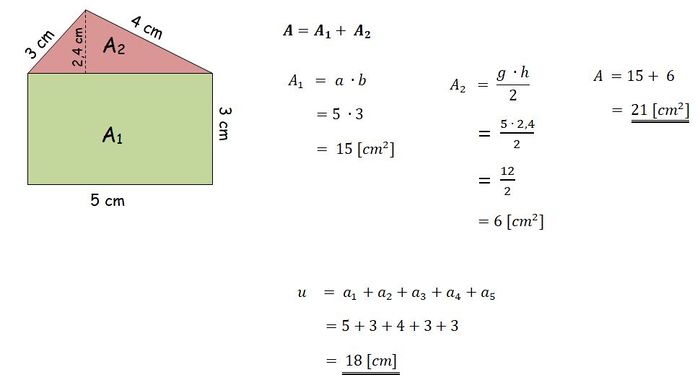
1b) in ein Rechteck und ein Dreieck
Kontrolliere deine Lösungen:
2a) Die Figur besteht aus 4 Drachenvierecken.
4 cm²; 8,5 cm²
7a) Das Hausdach setzt sich zusammen aus zwei Dreiecken und zwei Trapezen.
7b) Das Hausdach setzt sich zusammen aus zwei Dreiecken und 4 Trapezen, wobei je zwei Flächengleich sind.