Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Trapez: Unterschied zwischen den Versionen
K (Formel ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 30: | Zeile 30: | ||
{{#ev:youtube|w4SIXMBb0Ak|800|center}}<br><br> | {{#ev:youtube|w4SIXMBb0Ak|800|center}}<br><br> | ||
<br> | <br> | ||
Eine andere Möglichkeit ist die Berechnung mit Hilfe der sognenannten <span style="color: | Eine andere Möglichkeit ist die Berechnung mit Hilfe der sognenannten <span style="color:green">'''Mittellinie'''</span>. Hier ein Video zur Erklärung. | ||
{{#ev:youtube|wMLQ89-_qUs|800|center}}<br><br> | {{#ev:youtube|wMLQ89-_qUs|800|center}}<br><br> | ||
{{Box|1=Flächeninhalt und Umfang des Trapezes|2=[[Datei:Trapez allgemein.png|rechts|rahmenlos]]<br> | <nowiki>{{Box|1=Flächeninhalt und Umfang des Trapezes|2=</nowiki>[[Datei:Trapez allgemein.png|rechts|rahmenlos]]<br> | ||
Sind die a und c die parallelen Seiten des Trapezes und h die Höhe, wird der Flächeninhalt A eines Trapezes so berechnet:<br> | Sind die a und c die parallelen Seiten des Trapezes und h die Höhe, wird der Flächeninhalt A eines Trapezes so berechnet:<br> | ||
'''A = <math>\frac{\text{(a+c)h}}{\text{2}}</math>''' oder '''A = <math>\frac{\text{(a+c)}}{\text{2}}</math>∙h'''<br> oder <span style="color: | '''A = <math>\frac{\text{(a+c)h}}{\text{2}}</math>''' oder '''A = <math>\frac{\text{(a+c)}}{\text{2}}</math>∙h'''<br> oder <span style="color:green">'''A = m ∙ h'''</span> | ||
Der Umfang u eines Trapezes wird berechnet mit<br> | Der Umfang u eines Trapezes wird berechnet mit<br> | ||
| Zeile 63: | Zeile 63: | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">Umstellen nach der Seite a:<br> | <div class="width-1-2">Umstellen nach der Seite a:<br> | ||
A = <math>\frac{\text{a+c}}{\text{2}}</math>∙h |∙2<br> | A = <math>\frac{\text{a+c}}{\text{2}}</math>∙h |∙2<br>''' | ||
2∙A = (a+c)∙h |:h<br> | 2∙A = (a+c)∙h |:h<br> | ||
<math>\frac{\text{2A}}{\text{h}}</math> = a+c |-c<br> | <math>\frac{\text{2A}}{\text{h}}</math> = a+c |-c<br> | ||
| Zeile 69: | Zeile 69: | ||
Stelle die Formel entsprechend nach c um.<br> | Stelle die Formel entsprechend nach c um.<br> | ||
<div class="width-1-2">Umstellen nach der Höhe:<br> | <div class="width-1-2">Umstellen nach der Höhe:<br> | ||
A = <math>\frac{\text{a+c}}{\text{2}}</math>∙h |∙2<br> | A = <math>\frac{\text{a+c}}{\text{2}}</math>∙h |∙2<br> | ||
2∙A = (a+c)∙h |:(a+c)<br> | 2∙A = (a+c)∙h |:(a+c)<br> | ||
<math>\frac{\text{2A}}{\text{a+c}}</math> = h <br> | <math>\frac{\text{2A}}{\text{a+c}}</math> = h <br> | ||
</div> | </div> | ||
Version vom 6. März 2022, 07:33 Uhr
4.3) Trapez: Umfang und Flächeninhalt
1) Höhe im Trapez
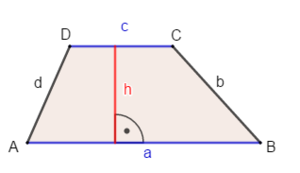
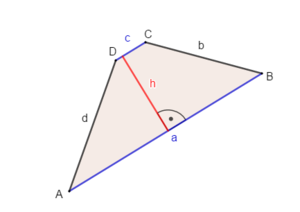
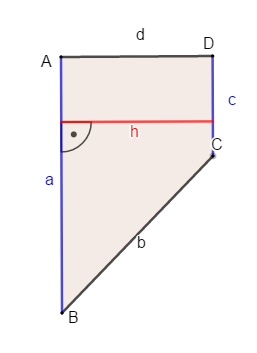
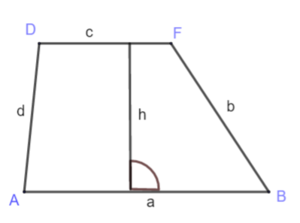
Die Höhe eines Trapezes ist der Abstand zwischen den parallelen Seiten. Schau, welche der Seiten parallel zueinander liegen und zeichne dazwischen die Höhe ein.
2) Formeln herleiten: Flächeninhalt A und Umfang u
Nun versuche, mithilfe des GeoGebra-Applets die Formel für den Flächeninhalt des Trapezes herzuleiten. Notiere deine Ideen.

Eine andere Möglichkeit ist die Berechnung mit Hilfe der sognenannten Mittellinie. Hier ein Video zur Erklärung.
{{Box|1=Flächeninhalt und Umfang des Trapezes|2=
Sind die a und c die parallelen Seiten des Trapezes und h die Höhe, wird der Flächeninhalt A eines Trapezes so berechnet:
A = oder A = ∙h
oder A = m ∙ h
Der Umfang u eines Trapezes wird berechnet mit
u = a + b + c + d.|3=Arbeitsmethode}}
Entnimm den Skizzen die nötigen Angaben für a, c und h. Setze dann in die Formel ein.
Vergleiche deine Lösungen (hier sind sie durcheinander angegeben):
Hier sind die Werte für a, c und h gegeben. Setze sie in die Formel ein und berechne.
3) Formeln umstellen
A = ∙h |∙2
2∙A = (a+c)∙h |:h
= a+c |-c
- c = a
Stelle die Formel entsprechend nach c um.
A = ∙h |∙2
2∙A = (a+c)∙h |:(a+c)
= h
Lösungen (gemischt) 0,9; 2,5; 7,2; 9; 14; 25; 75,6
4) Anwendungsaufgaben
Der Querschnitt des Kanals hat die Form eines Trapezes. Zeichne eine Skizze in dein Heft und beschrifte sie mit den angegebenen Maßen.
Lösung: 1386m²
Die gesamte Fläche der Backform setzt sich aus 5 Teilflächen zusammen:
Der Boden ist ein Rechteck.
Die Seiten der Backform sind jeweils Trapeze.
Skizziere die Flächen jeweils und beschrifte sie mit den angegebenen Maßen.
Zugabe von 10%
geg: G = 671cm²; p% = 10% = 0,1;
ges: W = G∙p%
W = 671 ∙ 0,1
W = 67,1 (cm²]
Dieser Wert muss also noch hinzugefügt werden.
(Du kannst auch mit dem Dreisatz rechnen:
100% | 671
Bestimme damit die Anzahl der Steine pro 1m² (=10000cm²).
Lösung: AStein=265cm²; ca.38 Steine
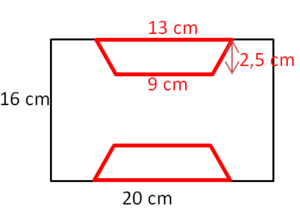
Bestimme den Flächeninhalt des Pflastersteins:
A = ARechteck - 2∙ATrapez
= 16∙20 - 2∙ ... wie kannst du den Flächeninhalt der Trapeze bestimmen?
Lösung: A = 265 cm², also hat ein Stein die Fläche von 265 cm². Wie viele solcher Steine passen in 1m² = 100dm² = 10000cm²?