Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Trapez: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (33 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Navigation|[[Benutzer:Buss-Haskert/Vierecke und Dreiecke| Einstieg und Vorwissen]]<br>[[Buss-Haskert/Vierecke und Dreiecke/Vierecke und ihre Eigenschaften|1) Vierecke und ihre Eigenschaften <br> 2) Haus der Vierecke]]<br>[[Buss-Haskert/Vierecke und Dreiecke/Winkelsumme|3) Winkelsumme im Viereck]]<br>[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt|4) Umfang und Flächeninhalt]]<br> | |||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt|4.1) Quadrat und Rechteck]]<br> | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt|4.1) Quadrat und Rechteck]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Parallelogramm|4.2) Parallelogramm]]<br> | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Parallelogramm|4.2) Parallelogramm]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/ | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Dreieck|4.3) Dreieck]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/ | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Trapez|4.4) Trapez]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen|4. | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen|4.5) Drachen]] | ||
*[[Buss-Haskert/Vierecke und Dreiecke/ | *[[Buss-Haskert/Vierecke und Dreiecke/Zusammengesetzte Figuren|4.6) Zusammengesetzte Figuren]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Bunte Mischung|4. | *[[Buss-Haskert/Vierecke und Dreiecke/Bunte Mischung|4.7) Bunte Mischung]]<br> | ||
[[Buss-Haskert/Vierecke und Dreiecke/Checkliste|5) Checkliste]]}} | |||
===4. | ===4.4) Trapez: Umfang und Flächeninhalt=== | ||
====1) Höhe im Trapez==== | ====1) Höhe im Trapez==== | ||
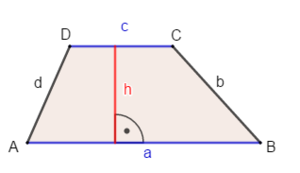
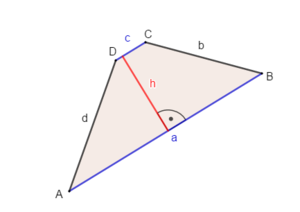
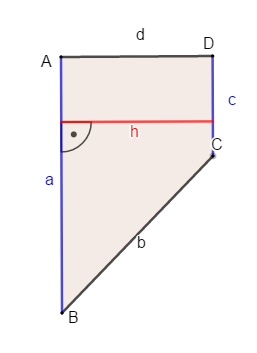
Die Höhe eines Trapezes ist der Abstand zwischen den parallelen Seiten. Schau, welche der Seiten parallel zueinander liegen und zeichne dazwischen die Höhe ein. | Die Höhe eines Trapezes ist der Abstand zwischen den parallelen Seiten. Schau, welche der Seiten parallel zueinander liegen und zeichne dazwischen die Höhe ein.<br> | ||
<div class="grid"> | |||
<div class="width-1-3">[[Datei:Trapez Höhe 1.png|rahmenlos]]</div> | |||
<div class="width-1-3">[[Datei:Trapez Höhe 2.png|rahmenlos]]</div> | |||
<div class="width-1-3">[[Datei:Trapez Höhe 3.png|rahmenlos]]</div> | |||
</div> | |||
{{Box|Übung 1: Höhe im Trapez|Kennzeichne auf dem AB jeweils die parallelen Seiten und zeichne die Höhe des Trapezes ein.|Üben}} | {{Box|Übung 1: Höhe im Trapez|Kennzeichne auf dem AB jeweils die parallelen Seiten und zeichne die Höhe des Trapezes ein.|Üben}} | ||
| Zeile 20: | Zeile 27: | ||
[[Datei:Idee_Flipchart.png|alternativtext=|links|rahmenlos|81x81px]] | [[Datei:Idee_Flipchart.png|alternativtext=|links|rahmenlos|81x81px]] | ||
Nun versuche, mithilfe des GeoGebra-Applets die Formel für den Flächeninhalt des Trapezes herzuleiten. Notiere deine Ideen.<br> | Nun versuche, mithilfe des GeoGebra-Applets die Formel für den Flächeninhalt des Trapezes herzuleiten. Notiere deine Ideen.<br> | ||
<ggb_applet id="M6dqPq6U" width=" | Originallink https://www.geogebra.org/m/M6dqPq6U | ||
<ggb_applet id="M6dqPq6U" width="150ö" height="700" border="888888" /> | |||
<small>Applet von Pöchtrager</small> | |||
<br> | |||
{{#ev:youtube|w4SIXMBb0Ak|800|center}}<br><br> | |||
Eine andere Möglichkeit ist die Berechnung mit Hilfe der sogenannten <span style="color:green">'''Mittellinie'''</span>. Hier ein Video zur Erklärung. | |||
{{#ev:youtube|wMLQ89-_qUs|800|center}}<br><br> | |||
{{Box|1=Flächeninhalt und Umfang des Trapezes|2=[[Datei:Trapez allgemein.png|rechts|rahmenlos]]<br> | {{Box|1=Flächeninhalt und Umfang des Trapezes|2=[[Datei:Trapez allgemein.png|rechts|rahmenlos]]<br> | ||
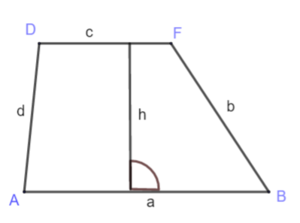
Sind die a und c die parallelen Seiten des Trapezes und h die Höhe, wird der Flächeninhalt A eines Trapezes so berechnet:<br> | Sind die a und c die parallelen Seiten des Trapezes und h die Höhe, wird der Flächeninhalt A eines Trapezes so berechnet:<br> | ||
'''A = <math>\frac{\text{(a+c)h}}{\text{2}}</math>''' oder '''A = <math>\frac{\text{(a+c)}}{\text{2}}</math> | '''A = <math>\frac{\text{(a+c)h}}{\text{2}}</math>''' oder '''A = <math>\frac{\text{(a+c)}}{\text{2}}</math> ∙ h''' oder <span style="color:green">'''A = m ∙ h'''</span> | ||
Der Umfang u eines Trapezes wird berechnet mit<br> | Der Umfang u eines Trapezes wird berechnet mit<br> | ||
'''u = a + b + c + d'''.|3=Arbeitsmethode}} | '''u = a + b + c + d'''.|3=Arbeitsmethode}} | ||
{{#ev:youtube|RBk6VlyANAw|800|center}} | |||
{{Box|Übung 2|Löse die nachfolgenden Learningapps. Schreibe die Aufgaben strukturiert in dein Heft.|Üben}} | {{Box|Übung 2|Löse die nachfolgenden Learningapps. Schreibe die Aufgaben strukturiert in dein Heft.|Üben}} | ||
| Zeile 34: | Zeile 50: | ||
{{Box|Übung 3|Löse Buch | {{Box|Übung 3|Löse Buch | ||
* S. 92 Nr. 1 | * S. 92 Nr. 1 | ||
* S. 92 Nr. 2a,c|Üben}} | * S. 92 Nr. 2a,c|Üben}}<br> | ||
{{Lösung versteckt|1=Entnimm den Skizzen die nötigen Angaben für a, c und h. Setze dann in die Formel ein. <br> | |||
Vergleiche deine Lösungen (hier sind sie durcheinander angegeben):<br> | |||
32,97cm²; 28,0cm²; 52,25cm²;46,48cm²|2=Vergleiche deine Lösungen zu Nr. 1|3=Verbergen}} | |||
{{Lösung versteckt|1=Hier sind die Werte für a, c und h gegeben. Setze sie in die Formel ein und berechne.<br> | |||
Lösungen (gemischt):63,0 cm²; 812,67cm²;85,5cm²;20,4dm²|2=Vergleiche deine Lösungen zu Nr. 2|3=Verbergen}} | |||
====3) Formeln umstellen==== | |||
<br> | |||
{{Box|Umstellen der Formel|Um die Länge einer der Seiten a und c oder der Höhe zu berechnen, muss die Formeln für den Flächeninhalt umgestellt werden. <br>1. Stelle die Flächeninhaltsformel um nach den Seitenlängen a und c.<br> | {{Box|Umstellen der Formel|Um die Länge einer der Seiten a und c oder der Höhe zu berechnen, muss die Formeln für den Flächeninhalt umgestellt werden. <br>1. Stelle die Flächeninhaltsformel um nach den Seitenlängen a und c.<br> | ||
<br>2. Stelle die Flächeninhaltsformel nach der Höhe um.|Üben}} | <br>2. Stelle die Flächeninhaltsformel nach der Höhe um.|Üben}} | ||
| Zeile 41: | Zeile 64: | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">Umstellen nach der Seite a:<br> | <div class="width-1-2">Umstellen nach der Seite a:<br> | ||
<math>\frac{\text{a+c}}{\text{2}}</math>∙h |∙2<br> | A = <math>\frac{\text{a+c}}{\text{2}}</math>∙h |∙2<br> | ||
2∙A = (a+c)∙h |:h<br> | 2∙A = (a+c)∙h |:h<br> | ||
<math>\frac{\text{2A}}{\text{h}}</math> = a+c |-c<br> | <math>\frac{\text{2A}}{\text{h}}</math> = a+c |-c<br> | ||
| Zeile 49: | Zeile 72: | ||
</div> | </div> | ||
<div class="width-1-2">Umstellen nach der Höhe:<br> | <div class="width-1-2">Umstellen nach der Höhe:<br> | ||
<math>\frac{\text{a+c}}{\text{2}}</math>∙h |∙2<br> | A = <math>\frac{\text{a+c}}{\text{2}}</math>∙h |∙2<br> | ||
2∙A = (a+c)∙h |:(a+c)<br> | 2∙A = (a+c)∙h |:(a+c)<br> | ||
<math>\frac{\text{2A}}{\text{a+c}}</math> = h <br> | <math>\frac{\text{2A}}{\text{a+c}}</math> = h <br> | ||
</div> | </div> | ||
</div> | </div> | ||
<br> | |||
{{Box|Übung 4: Formel umstellen|Löse die nachfolgende LearningApp. Schreibe die Aufgabe strukturiert in dein Heft.|Üben}} | |||
{{Box| | |||
{{LearningApp|app=p5q3qzoq319|width=100%|heigth=600px}} | {{LearningApp|app=p5q3qzoq319|width=100%|heigth=600px}} | ||
| Zeile 64: | Zeile 86: | ||
* S. 96 Nr. 4 | * S. 96 Nr. 4 | ||
Notiere die Formel und stelle sie nach der gesuchten Größe um. Setze dann ein und berechne.|Üben}} | Notiere die Formel und stelle sie nach der gesuchten Größe um. Setze dann ein und berechne.|Üben}} | ||
{{Lösung versteckt|1=Lösungen (gemischt) 0,9; 2,5; 7,2; 9; 14; 25; 75,6<br> | |||
Achte auf die richtige Einheit im Ergebnis.|2=Vergleiche deine Lösungen|3=Verbergen}} | |||
====4) Anwendungsaufgaben==== | ====4) Anwendungsaufgaben==== | ||
{{Box|Übung 6: Anwendungsaufgaben zu Trapezen|Löse die Anwendungsaufgaben übersichtlich. Notiere zunächst die gegebenen Größen. Zeichne eine Skizze und beschrifte diese. Überlege, was gesucht ist. Unterscheide zwischen Flächen'''in'''halt A('''in'''nen dr'''in''') und '''Um'''fang u (dr'''um''' her'''um'''). | {{Box|Übung 6: Anwendungsaufgaben zu Trapezen|Löse die Anwendungsaufgaben übersichtlich. Notiere zunächst die gegebenen Größen. Zeichne eine Skizze und beschrifte diese. Überlege, was gesucht ist. Unterscheide zwischen Flächen'''in'''halt A('''in'''nen dr'''in''') und '''Um'''fang u (dr'''um''' her'''um'''). | ||
| Zeile 79: | Zeile 102: | ||
Lösung: 671 cm²|2=Tipp 1 zu Nr. 7|3=Verbergen}} | Lösung: 671 cm²|2=Tipp 1 zu Nr. 7|3=Verbergen}} | ||
{{Lösung versteckt|1=Zugabe von 10%<br> | {{Lösung versteckt|1=Zugabe von 10%<br> | ||
geg: G = 671cm²; p% = 10% = 0,1; | geg: G = 671cm²; p% = 10% = 0,1; <br> | ||
ges: W = G∙p%<br> | |||
W = 671 ∙ 0,1<br> | |||
{{Lösung versteckt|1=Die Fläche des Steins entspricht der Fläche des großen Rechtecks minus den 2 kleinen Trapezflächen. Zeichne eine Skizze in dein Heft und beschrifte sie vollständig. Berechne dann die Fläche eines Steines. <br>Bestimme damit die Anzahl der Steine pro 1m² (=10000cm²).<br>Lösung: A<small>Stein</small>=265cm²; ca.38 Steine|2=Tipp zu Nr. 8|3=Verbergen}} | W = 67,1 (cm²]<br> | ||
Dieser Wert muss also noch hinzugefügt werden.<br> | |||
(Du kannst auch mit dem Dreisatz rechnen:<br> | |||
100% | 671<br> | |||
10% |67,1<br> | |||
|2=Tipp 2 zu Nr. 7|3=Verbergen}} | |||
{{Lösung versteckt|1=Die Fläche des Steins entspricht der Fläche des großen Rechtecks minus den 2 kleinen Trapezflächen. Zeichne eine Skizze in dein Heft und beschrifte sie vollständig. Berechne dann die Fläche eines Steines. <br>Bestimme damit die Anzahl der Steine pro 1m² (=10000cm²).<br>Lösung: A<small>Stein</small>=265cm²; ca.38 Steine|2=Tipp 1 zu Nr. 8|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:Skizze zu S.92 Nr. 8.png|rahmenlos]]<br> | |||
Bestimme den Flächeninhalt des Pflastersteins:<br> | |||
A = A<sub>Rechteck</sub> - 2∙A<sub>Trapez</sub><br> | |||
= 16∙20 - 2∙ ... wie kannst du den Flächeninhalt der Trapeze bestimmen?<br> | |||
Lösung: A = 265 cm², also hat ein Stein die Fläche von 265 cm². Wie viele solcher Steine passen in 1m² = 100dm² = 10000cm²?<br> | |||
Lösung ca. 38.|2=Tipp 2 zu Nr. 8|3=Verbergen}} | |||
{{Box|Noch mehr Übungen|Du findest weitere Übungen auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/viereck/trapez.shtml '''Aufgabenfuchs'''].|Üben}} | |||
{{Fortsetzung|vorher=4.3) Dreieck|vorherlink=Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Dreieck}} | |||
{{Fortsetzung|weiter=4) | Für die schnellen Rechner: | ||
{{Fortsetzung|weiter=4.5) Drachen (Deltoid)|weiterlink=Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen}} | |||
<br> | |||
<br> | |||
Du kannst das Kapitel zum Drachen überspringen, um Zeit zu sparen. Gehe sofort weiter zu den gemischten Übungsaufgaben. | |||
{{Fortsetzung|weiter=4.6) Bunte Mischung|weiterlink=Buss-Haskert/Vierecke und Dreiecke/Bunte Mischung}} | |||
Aktuelle Version vom 20. November 2024, 16:13 Uhr
1) Vierecke und ihre Eigenschaften
2) Haus der Vierecke
3) Winkelsumme im Viereck
4) Umfang und Flächeninhalt
- 4.1) Quadrat und Rechteck
- 4.2) Parallelogramm
- 4.3) Dreieck
- 4.4) Trapez
- 4.5) Drachen
- 4.6) Zusammengesetzte Figuren
- 4.7) Bunte Mischung
4.4) Trapez: Umfang und Flächeninhalt
1) Höhe im Trapez
Die Höhe eines Trapezes ist der Abstand zwischen den parallelen Seiten. Schau, welche der Seiten parallel zueinander liegen und zeichne dazwischen die Höhe ein.
2) Formeln herleiten: Flächeninhalt A und Umfang u
Nun versuche, mithilfe des GeoGebra-Applets die Formel für den Flächeninhalt des Trapezes herzuleiten. Notiere deine Ideen.
Originallink https://www.geogebra.org/m/M6dqPq6U

Applet von Pöchtrager
Eine andere Möglichkeit ist die Berechnung mit Hilfe der sogenannten Mittellinie. Hier ein Video zur Erklärung.
Entnimm den Skizzen die nötigen Angaben für a, c und h. Setze dann in die Formel ein.
Vergleiche deine Lösungen (hier sind sie durcheinander angegeben):
Hier sind die Werte für a, c und h gegeben. Setze sie in die Formel ein und berechne.
3) Formeln umstellen
A = ∙h |∙2
2∙A = (a+c)∙h |:h
= a+c |-c
- c = a
Stelle die Formel entsprechend nach c um.
A = ∙h |∙2
2∙A = (a+c)∙h |:(a+c)
= h
Lösungen (gemischt) 0,9; 2,5; 7,2; 9; 14; 25; 75,6
4) Anwendungsaufgaben
Der Querschnitt des Kanals hat die Form eines Trapezes. Zeichne eine Skizze in dein Heft und beschrifte sie mit den angegebenen Maßen.
Lösung: 1386m²
Die gesamte Fläche der Backform setzt sich aus 5 Teilflächen zusammen:
Der Boden ist ein Rechteck.
Die Seiten der Backform sind jeweils Trapeze.
Skizziere die Flächen jeweils und beschrifte sie mit den angegebenen Maßen.
Zugabe von 10%
geg: G = 671cm²; p% = 10% = 0,1;
ges: W = G∙p%
W = 671 ∙ 0,1
W = 67,1 (cm²]
Dieser Wert muss also noch hinzugefügt werden.
(Du kannst auch mit dem Dreisatz rechnen:
100% | 671
Bestimme damit die Anzahl der Steine pro 1m² (=10000cm²).
Lösung: AStein=265cm²; ca.38 Steine
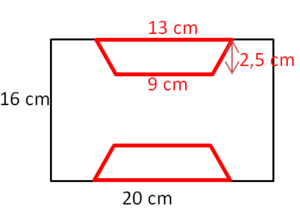
Bestimme den Flächeninhalt des Pflastersteins:
A = ARechteck - 2∙ATrapez
= 16∙20 - 2∙ ... wie kannst du den Flächeninhalt der Trapeze bestimmen?
Lösung: A = 265 cm², also hat ein Stein die Fläche von 265 cm². Wie viele solcher Steine passen in 1m² = 100dm² = 10000cm²?
Für die schnellen Rechner:
Du kannst das Kapitel zum Drachen überspringen, um Zeit zu sparen. Gehe sofort weiter zu den gemischten Übungsaufgaben.