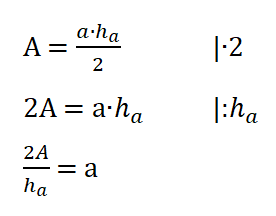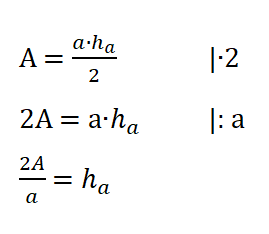Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Dreieck: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 137: | Zeile 137: | ||
* S. 90 Nr. 15 | * S. 90 Nr. 15 | ||
Nutze als Hilfe die nachfolgende Applets. Was geschieht mit dem Flächeninhalt und dem Umfang des Dreiecks. Notiere und erkläre.|Üben}} | Nutze als Hilfe die nachfolgende Applets. Was geschieht mit dem Flächeninhalt und dem Umfang des Dreiecks. Notiere und erkläre.|Üben}} | ||
<ggb_applet id="s6gkebvn" width="911" height="507" border="888888" / | <ggb_applet id="s6gkebvn" width="911" height="507" border="888888" /> | ||
<ggb_applet id="fm2qyyjz" width="767" height="507" border="888888" / | <ggb_applet id="fm2qyyjz" width="767" height="507" border="888888" /> | ||
<ggb_applet id="te6w3afp" width="911" height="507" border="888888" / | <ggb_applet id="te6w3afp" width="911" height="507" border="888888" /> | ||
<small>Applets von C.Buß-Haskert</small> | <small>Applets von C.Buß-Haskert</small><br> | ||
Für die schnellen Rechner: | Für die schnellen Rechner: | ||
{{Fortsetzung|weiter=5) Drachen (Deltoid)|weiterlink=Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen}} | {{Fortsetzung|weiter=5) Drachen (Deltoid)|weiterlink=Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen}} | ||
Version vom 27. November 2022, 12:08 Uhr
4.4) Dreieck: Umfang und Flächeninhalt
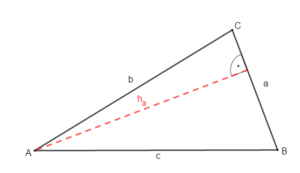
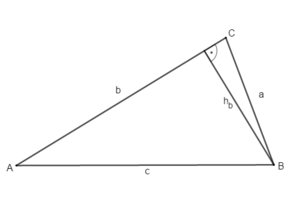
1) Höhen im Dreieck
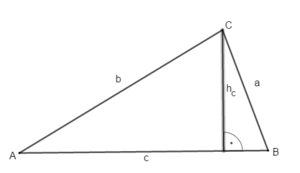
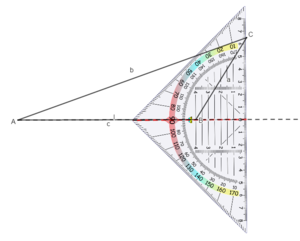
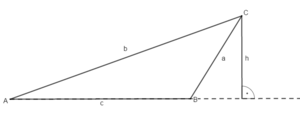
Wiederhole zunächst die Bezeichnungen am Dreieck. Übertrage die Zeichnung in dein Heft.

Verschiebe im nachfolgenden Applet die Punkte und beobachte die Lage der Höhen. Was fällt dir auf?

Die Höhen stehen senkrecht auf den Dreiecksseiten und verlaufen durch den gegenüberliegenden Eckpunkt.
Die Höhen schneiden sich in einem Punkt.
Zeichne die Höhe hc zur Seite c:
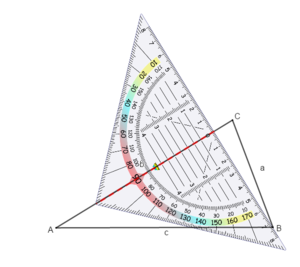
Zeichne ebenso die Höhe ha zur Seite a:
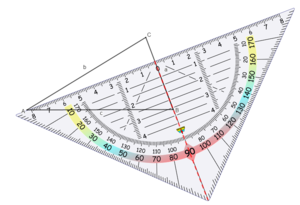
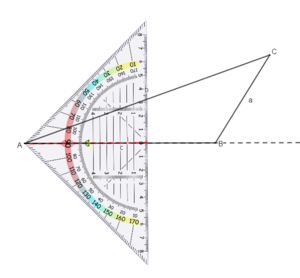
... und die Höhe hb zur Seite b:
In einem stumpfwinkligen Dreieck verlaufen die Höhen teils außerhalb des Dreiecks. Die Dreiecksseite muss verlängert werden, um die Höhe einzeichnen zu können:
Übe zunächst das Einzeichnen der Höhen mit dem nachfolgenden Applet:

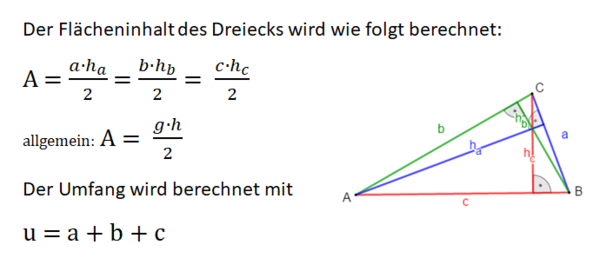
2) Formeln herleiten: Flächeninhalt A und Umfang u
Nun versuche, mithilfe des GeoGebra-Applets die Formel für den Flächeninhalt eines Dreiecks herzuleiten. Notiere deine Ideen.
Bearbeite die nachfolgenden Applets Schritt für Schritt.



Du kannst die Formel für den Flächeninhalt eines Dreiecks auch anders herleiten:



Entnimm den Skizzen bzw. der Aufgabenstellung die nötigen Maße und setze sie in die Formel ein.
3) Formeln umstellen

Notiere die Formel und stelle sie nach der gesuchten Größe um. Setze dann die Zahlen ein und bereche.
Lösungen (gemischt): 6; 10,5; 12; 13,5; 14; 18; 30; 36
4) Anwendungsaufgaben
Die Holzverkleidung hat die Form eines Dreiecks mit der Grundseite g=1,5m und der Höhe h=3,7-2,2=1,5(m).
Lösung zur Kontrolle:AHolz=1,125m²
Das Fenster hat die Form eines Trapezes mit den Seiten c=1,1+1,5+1,5=3,7(m), a=1,5(m) und der Höhe h=2,2(m).
Du kannst die Glasfläche auch als zusammengesetzte Fläche betrachten:
Ein Rechteck in der Mitte und zwei Dreiecke außen.
Lösung zur Kontrolle:A=5,72m²
Um die Kosten zu berechnen, multipliziere jeweils die Fläche mit dem Preis pro m².
Eine Dreiecksfläche hat die Grundseite g=5,2m und die Höhe h=7,35m. Die andere Zahlenangabe ist für die Lösung dieser Aufgabe überflüssig!
Um die Kosten zu berechnen, multipliziere die Dachfläche mit dem Preis pro m²
a=44,8(m), h=b=58,5m, also beträgt der Flächeninhalt des Dreiecks 1310,4m².
Die Fläche des Rechteck des Schulgebäudes (236,25m²) muss nun von dieser Fläche abgezogen werden.



Applets von C.Buß-Haskert
Für die schnellen Rechner:
Du kannst das Kapitel zum Drachen überspringen, um Zeit zu sparen. Gehe sofort weiter zu den gemischten Übungsaufgaben.