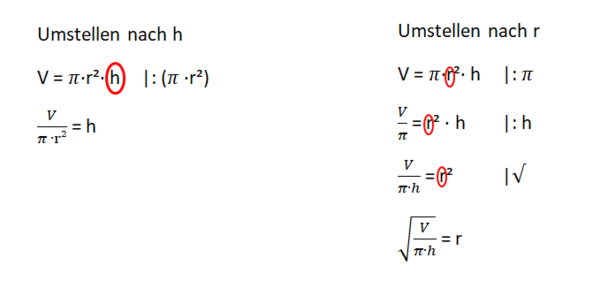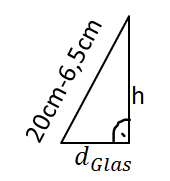Benutzer:Buss-Haskert/Kreis und Zylinder/Zylinder

zurück zur Seite der Herta-Lebenstein-Realschule

Kreis und Zylinder - Startseite

1 Kreisumfang
2 Kreisfläche
3 Kreisteile
4 Zylinder
5 Zusammengesetzte Körper

Zylinder

Zylinder - Eigenschaften

Beschreibe die Eigenschaften eines Zylinders. Nutze dazu die nachfolgenden Applets.

Applet von T. Traub

Applet von B. Lachner

Zylinder - Eigenschaften

Ein Zylinder ist ein Körper mit zwei deckungsgleichen (kongruenten) Kreisflächen als Grund- und Deckfläche und einem Rechteck als Mantelfläche.

Zylinder Einführung - Aufbau und Bestandteile (Geometrie)

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1

<a href="/wiki/Datei:Kreiszylinder.svg" class="image"><img alt="Kreiszylinder.svg" src="https://upload.wikimedia.org/wikipedia/commons/thumb/4/4d/Kreiszylinder.svg/langde-479px-Kreiszylinder.svg.png" decoding="async" width="479" height="170" srcset="https://upload.wikimedia.org/wikipedia/commons/thumb/4/4d/Kreiszylinder.svg/langde-719px-Kreiszylinder.svg.png 1.5x, https://upload.wikimedia.org/wikipedia/commons/thumb/4/4d/Kreiszylinder.svg/langde-958px-Kreiszylinder.svg.png 2x" data-file-width="479" data-file-height="170"></a><br> Kreuze Eigenschaften eines geraden Zylinders an!

1. Grund- und Deckfläche sind Kreise
2. Grund- und Deckfläche liegen parallel zueinander
3. Mantelfläche: ein Trapez
4. Körperhöhe gleich Abstand der Kreise
5. n-Eck als Grundfläche
6. Grund- und Deckfläche: kongruent

prüfen!

neu starten

Übung 2

Fülle die Lücken passend aus ("Schüttelwörter").

Die Oberfläche eines Zylinders besteht aus (fcnguhläedr), (ekclceäfhd) und (lmeäfcelthan). Die Grund- und Deckfläche ist ein (eiksr), die Mantelfläche ein (cthecekr).

neu starten

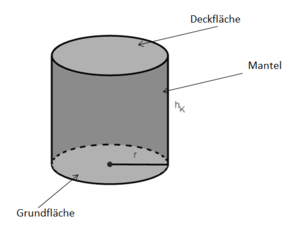
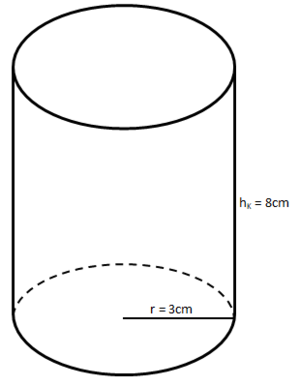
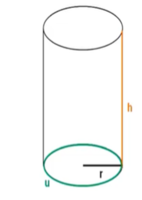
Schrägbild und Netz eines Zylinders

Das Applet zeigt dir, wie du die Schrägbilder eines Zylinders zeichnen kannst, im Video wird dies noch einmal erklärt.
Originallink: https://www.geogebra.org/m/y73hvejn

Um das Schrägbild eines Zylinders für deinen Hefteintrag zeichnen zu können, schau das nachfolgenden Video an:

B6 Ich zeichne Schrägbilder von Zylindern

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Applet von R. Herzog, Wolfgang Wengler
Wenn du magst (freiwillig), kannst du für eine bessere Vorstellung einen Zylinder basteln. (AB liegt auf dem Pult) https://www.zum.de/dwu/mkb031vs.htm

Netz und Schrägbild eines Zylinders

Zeichne das Netz und das Schrägbild eines Zylinders in dein Heft mit r=3,0cm und h=8cm.

Übung 3:Entstehung von Drehkörpern

• S. 140 Nr. 5 Beschreibe mithilfe des Applets unten, wie ein Zylinder entsteht.
• S. 140 Nr. 6

Oberfläche eines Zylinders

Oberfläche eines Zylinders

Leite mithilfe des Netzes eines Zylinders eine Formel für die Oberfläche her.

• Aus welchen Teilflächen setzt sich die Oberfläche zusammen?
• Wie lauten die Formeln für den jeweiligen Flächeninhalt?

Tipp 1

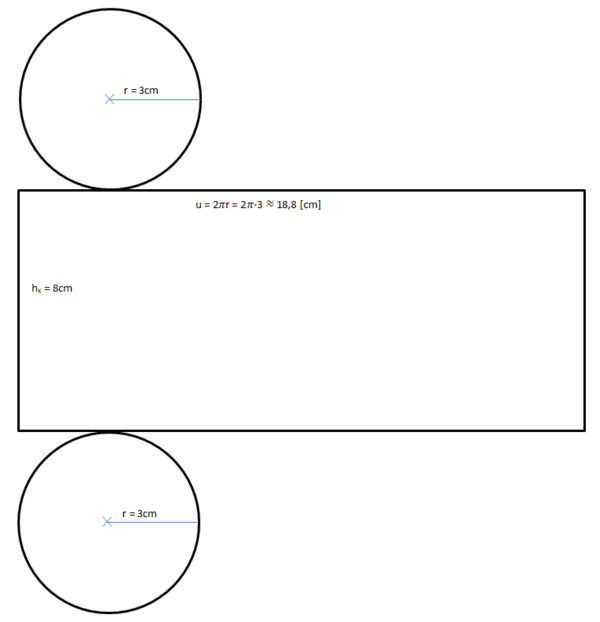
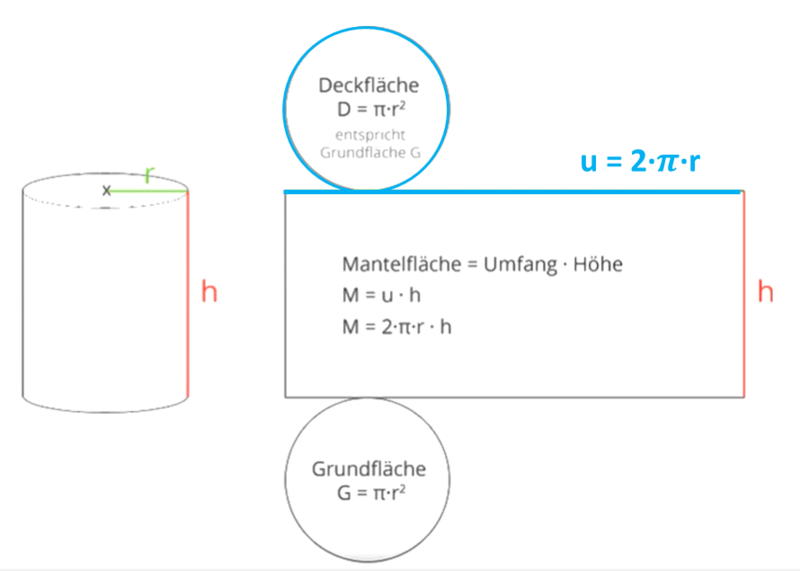
Die Oberfläche setzt sich zusammen aus der Grund- und Deckfläche und der Mantelfläche.

Also: O = 2·G + M

Tipp 2

Die Grund- und Deckfläche ist ein Kreis. Die Formel für den Flächeninhalt des Kreises lautet
G = π·r².
Die Mantelfläche ist ein Rechteck. Der Flächeninhalt berechnet sich also mit

M = Länge · Breite

Tipp 3

Die Länge des Rechtecks ist der Umfang u des Kreises, also u = 2·π·r.
Die Breite des Rechtecks ist die Körperhöhe h_K.
Also gilt:
M =u·h_K

   = 2πr·h_K

Oberfläche eines Zylinders

Die Oberfläche eines Zylinders wird mit folgender Formel berechnet:
O = 2·G + M
   = 2·π·r² + u·h_K
   = 2πr² + 2πr·h_K

Zusammenfassung:

Zylinder Einführung - Aufbau und Bestandteile (Geometrie)

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Zylinder - Oberfläche berechnen | Körper | Mathematik | Lehrerschmidt

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Beispiele:
geg: r = 5cm; h = 7cm
ges: M und O
M = 2πr·h   |Werte einsetzen
   = 2π·5·7
   = 219,91 (cm²)
O = 2πr² + 2πr·h   |Werte einsetzen
   = 2π·5² + 2π·5·7
   = 376,99 (cm²)

Achte auf die Einheiten: M und O sind Flächen, also cm²

Übung 4

Löse die Aufgaben aus dem Buch. Notiere deine Rechnungen übersichtlich.

• S. 142 Nr. 1 (Wähle zwei Aufgaben aus.)
• S. 142 Nr. 2 (Vorsicht Druckfehler, O = 5,5 m²)

Umstellen der Mantelformel

Mantelformel:

Umstellen der Oberflächenformel (nach h)

Oberflächenformel:

Prüfe deine Lösungen:

Übung 5

Löse auf der Seite Aufgabenfuchs die nachfolgenden Aufgaben. Schreibe die Rechnungen in dein Heft und überprüfe deine Lösung.

• 10
• 11
• 12

Volumen eines Zylinders

Volumen eines Zylinders

Leite eine Formel für das Volumen des Zylinders her, das GeoGebra-Applet hilft dir.

• Mit dem roten Mittelpunkt kannst du die Höhe verändern.
• Mit der roten Ecke drehst du das Prisma.
• Die beiden Schieberegler verändern den Radius bzw. die Anzahl Ecken.

Aufgabe: Verändere die Anzahl Ecken des Prismas und beobachte die beiden Volumenangaben. Was stellst du fest?

Volumen eines Zylinders

Die Formel für das Volumen eines Zylinders lautet

V = G · h_K

   = π·r²·h_K

Achte auf die Einheit: V ist das Volumen, also cm³

Übung 6

Löse auf der Seite Aufgabenfuchs die nachfolgenden Aufgaben. Schreibe die Rechnungen in dein Heft und überprüfe deine Lösung.

• 3
• 4

Übung 7

Löse die Aufgaben aus dem Buch. Achte auf eine übersichtliche Darstellung.

• S. 145 Nr. 1 (Wähle zwei Aufgaben aus.)
• S. 145 Nr. 2 (Wähle zwei Aufgaben aus.)
• S. 145 Nr. 3 (Wähle drei Aufgaben aus.(Nr. 3f ***)

Volumeneinheiten

Volumeneinheiten:
Erinnerung: 1dm³ = 1 Liter

1 dm3 is 1 liter

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Volumenformel umstellen

Höhe und Radius eines Zylinders berechnen | Fundamente der Mathematik | Erklärvideo

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Tipp zu 3f

Du hast die Mantelfläche und das Volumen gegeben. Beide Formeln enthalten die Variablen r und h.
Löse durch Einsetzen.
Z.B. M = 2πrh   | : (2πr)
$\tfrac{M}{2\pi r} = \tfrac{350}{2\pi r}$ = h
Ersetze nun in der Volumenformel das h durch diesen Term:
V = πr²h   |h = $\tfrac{M}{2\pi r}$ einsetzen
V = πr²$\tfrac{M}{2\pi r}$   | kürzen
V = r$\tfrac{M}{2}$
Stelle die Formel nun nach r um und setze die gegebene Werte für V und M ein.

r = 3,2 (cm)

Vergleiche deine Lösungen zu Nr. 1,2,3

Vergleiche deine Lösungen (unsortiert): Denke an die passende EINHEIT!

2,2; 3,1; 3,1; 3,2; 3,9; 3,9; 4,9; 7,1; 8,7; 17,4; 45,8; 123,8; 190,9; 311,0; 338,2; 414,3; 461,9; 471,2; 508,4; 659,5; 777,8; 794,3; 1200,7; 1296,3; 1750,4; 4065,1; 4825,5; 5541,8; 33846,3; 961433,5

Übung 8

Verändere im Applet unten den Radius und die Höhe des Zylinders und beobachte, wie die Oberfläche bzw. das Volumen sind ändert. Löse anschließend aus dem Buch.

• S.143, Nr. 3 (Nutze das Applet unten)
• S.145, Nr. 4 (Nutze das Applet unten)
• S.145, Nr. 10
• S.145, Nr. 9

Zu Nr. 3
Originallink: https://www.geogebra.org/m/drdmxpef

Zu Nr. 4
Originallink: https://www.geogebra.org/m/werggqdn

Tipp zu Nr. 10

geg: V = 144π cm³ = 452,4 (cm³)
Stelle die Volumenformel nach r um und berechne so jeweils die Höhe des Zylinders.

Anschließend kannst du mit diesen Größen die Oberfläche bestimmen.

Applet zu Nr. 9a
Originallink: https://www.geogebra.org/m/vckecqmu

Rechnerische Begründung zu 9a

Rechnerische Begründung:
M₁ = 2πrh; M₂ = 2πr·2h = 2·(2πrh) = 2·M₁

Ebenso V...

Applet zu Nr. 9b
Originallink: https://www.geogebra.org/m/c9gtayuk

Rechnerische Begründung zu 9b

Rechnerische Begründung:
M₁ = 2πrh; M₂ = 2π·2r·h = 2·(2πrh) = 2·M₁

V₁ = πr²h; V₂ = π·(2r)²·h = π·2²r²·h = π·4r²·h = 4·V₁

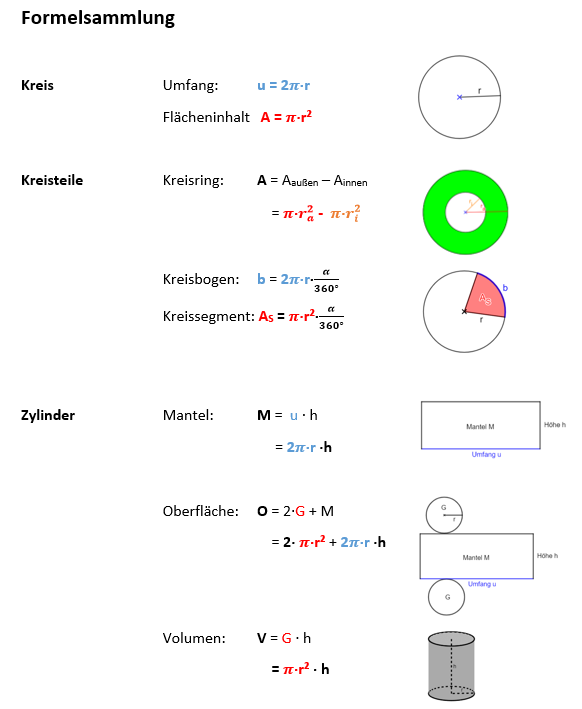
Formelsammlung

Fasse alle Formeln in einer Formelsammlung zusammen.
Du musst nur zwei Formeln auswendig lernen: Umfang und Flächeninhalt des Kreises! Alle anderen Formeln werden daraus abgeleitet.
Erkläre die Bedeutung der Farben (blau und rot).

Anwendungen

Entscheide, ob die Mantelfläche, die Oberfläche oder das Volumen des Zylinders gesucht ist.

Übung 9

Löse so viele Aufgaben, dass du mindestes 7 Sternchen sammelst. Notier deine Rechnungen ausführlich und übersichtlich. Prüfe deine Lösungen und hake ab.

• S. 143, Nr. 7 (*)
• S. 143, Nr. 8 (*)
• S. 143, Nr. 4 (**)
• S. 145, Nr. 5 (**)
• S. 145, Nr. 6 (**)
• S. 145, Nr. 7 (**)
• S. 143, Nr. 9 (***)

Tipp 1 zu S. 143, Nr. 7

Es muss nur einmal die Grundfläche gestrichen werden, die andere Fläche steht ja in der Erde.
Achte auf gleiche Einheiten!

Skizze:

Tipp 2 zu S. 143, Nr. 7

geg: 26 Pfähle; je d=15cm, also r=d:2=7,5cm; h=1,10m=110cm (gleiche Einheit!)
ges: anzustreichende Fläche

A = (1·G + M)·26

Vergleiche deine Lösungen zu S. 143, Nr. 7

Lösung: 13,94m² ≈ 14m², also ca. 7Liter Farbe

Tipp zu S. 143 Nr. 8

Die Dachfläche entspricht der Mantelfläche eines ganzen Zylinders. Wie groß ist sein Radius?

Vergleiche deine Lösung zu S. 143 Nr. 8

Lösung: ≈310,70 m²

Tipp zu S. 143, Nr. 4b

18% Verschnitt bedeutet, dass 18% mehr Material benötigt wird.

Erinnerung: Formel G⁺ = G · p⁺% oder Dreisatz.

Tipp zu S. 143 Nr. 4c

Skizze:

Vergleiche deine Lösungen zu S. 143, Nr. 4

a) O ≈ 518,36 cm²; b) Materialbedarf ≈ 611,67 cm² c) Höhe: 10,9 cm; Breite: ≈ 32,62 cm; A = 355,56 cm²

Tipp zu S. 145, Nr. 5a

Achte auf gleiche Einheiten!

Grundformel der Prozentrechnung: W = G · p% (Wie Geht prozentrechnung?, die Rechtschreibung ist falsch, alles für die Mathematik)

Tipp zu S. 145 Nr. 5b

Erinnerung: 1dm³ = 1 Liter

Stelle die Volumenformel nach h um.

Vergleiche deine Lösungen zu S. 145, Nr. 5

a) V ≈ 482,6 l; b) h≈ 9,0 dm

Tipps zu S. 145, Nr. 6

Tipps:
- Bestimme das Volumen der Apfelsafttüte (Quader!, V = a · b · c)
- Bestimme das Volumen des Zylinders

- Vergleiche die Volumina.

Vergleiche deine Lösungen zu S. 145 Nr. 6

Lösung: Ja, es passt (V_Tüte = 1004,5cm³ und V_Krug=1005,3 cm³)

Tipp zu S. 145, Nr. 7

Bestimme die Höhe mit dem Satz des Pythagoras.

Vergleiche deine Lösungen zu S. 145, Nr. 7

Lösung: h ≈ 12,1cm; V ≈342,1cm³ = 342,1ml

Tipps zu S. 143, Nr. 9

Tipps:

 - die Außen- bzw. Innenfläche entspricht der Mantelfläche

- berechne die innere Mantelfläche

- berechne damit die äußere Mantelfläche (10% mehr)

- bestimme damit den Radius des äußeren Zylinders

- Rohrdicke = Außenradius - Innenradius

Vergleiche dein Lösung zu S. 143, Nr. 9

Lösung: Dicke = 0,25 cm

Formelsammlung:

5) Zusammengesetzte Körper