Benutzer:Buss-Haskert/Kreis und Zylinder/Zusammengesetzte Körper

zurück zur Seite der Herta-Lebenstein-Realschule

Kreis und Zylinder - Startseite

1 Kreisumfang
2 Kreisfläche
3 Kreisteile
4 Zylinder
Benutzer:Buss-Haskert/Kreis und Zylinder/Zusammengesetzte Körper

5) Zusammengesetzte Körper

Einstiegsaufgabe

Du machst ein Praktikum im Bereich Metallbau und sollst den folgenden Doppelzylinder und den ausgeborten Zylinder fräsen.

Welche (mathematische) Fragen kannst du an diese Aufgabe stellen? Notiere deine Ideen im Heft und tausche dich anschließend mit deinem Sitznachbarn aus.

Mögliche Fragen könnten sein:
- Welches Volumen hat dieser Körper?
- Welche Oberfläche hat dieser Körper?

- Wie schwer ist das Werkstück, wenn er aus Eisen besteht, wenn Eisen die Dichte von ca. 7,9 $\tfrac{g}{cm^3}$ besitzt?

Berechnung des Volumens:
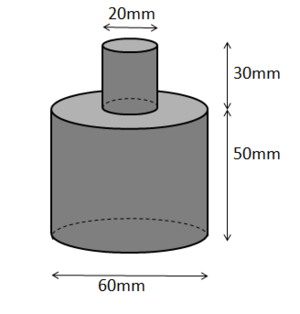
Das Volumen des Doppelzylinders ergibt sich aus der Summe der beiden einzelnen Volumina.
V = V_oben + V_unten
Bestimme die Radien der Zylinder mithilfe der gegebene Durchmesser. Die Höhen sind ebenfalls gegeben.

Vergleiche deine Lösung: V = 150796,45 mm³

Berechnung der Oberfläche:
Stelle dir vor, du hältst den Doppelzylinder unter den Wasserhahn, welche Flächen werden nass?
Diese Flächen ergeben die Oberfläche des zusammengesetzten Körpers.
Die Oberfläche des Doppelzylinders setzt sich zusammen aus der Oberfläche des unteren Zylinders und der Mantelfläche des oberen Zylinders.
O = O_unten + M_oben
Ebenso könnte man die Oberflächen beider Zylinder berechnen und dann die beiden Kreisflächen, bei denen sich die Körper berühren, wieder subtrahieren.
O = O_unten + O_oben - 2G_oben

Vergleiche deine Lösung: O = 1694,6 mm²

Berechnung des Volumens:
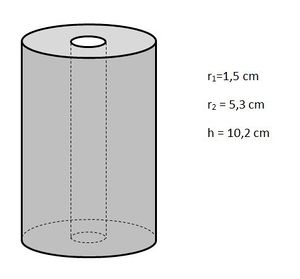
Das Volumen des ausgefrästen Zylinders ergibt sich aus der Differenz der beiden einzelnen Volumina.
V = V_außen - V_innen
Die Radien der Zylinder sind gegeben, die Höhe ist bei beiden Zylindern gleich.

Vergleiche deine Lösung: V = 828,02 cm³

Berechnung der Oberfläche:
Stelle dir vor, du hältst den ausgefrästen Zylinder unter den Wasserhahn, welche Flächen werden nass?
Diese Flächen ergeben die Oberfläche des zusammengesetzten Körpers.
Die Oberfläche des ausgefrästen Zylinders setzt sich zusammen aus der Oberfläche des äußeren Zylinders ohne die zwei Grundflächen des inneren Zylinders und der Mantelfläche des inneren Zylinders.
O = O_außen - 2G_innen + M_innen
Ebenso könnte man die Oberflächen beider Zylinder berechnen und dann 4 mal die Grundfläche des inneren Zylinders subtrahieren.
O = O_außen + O_innen - 4G_innen

Vergleiche deine Lösung: O = 598,16 cm²

Übung 1

Kreuze die richtigen Formeln zur Berechnung der Oberfläche der zusammengesetzten Körper an.

(Erinnerung: Die Oberfläche setzt sich aus allen Flächen zusammen, die beim Eintauchen in Wasser nass werden.)

Übung 2

Löse die nachfolgende LearningApp. Notiere die Rechnungen ausführlich im Heft.

Übung 3

Wähle eine Aufgabe der folgenden Aufgaben aus und löse ausführlich. Trage deine Lösung der Klasse vor. Überlege, wie du deine Lösung präsentieren möchtest.

• S. 148, Nr. 2
• S. 148. Nr. 3
• S. 148, Nr. 4
• S. 148, Nr. 5
• S. 148, Nr. 6

Notiere zunächste die gegebenen und gesuchten Größen!
Erkläre dann die Möglichkeiten, die Oberfläche zu berechnen:
1. Möglichkeit:
O_Körper = O_{Zylinder groß} + M_{Zylinder klein} - 2·G_{Zylinder klein}

2. Möglichkeit:
O_Körper = O_{Zylinder groß} + O_{Zylinder klein} - 4·G_{Zylinder klein}

3. Möglichkeit:
O_Körper = 2·(G_{Zylinder groß} - G_{Zylinder klein}) + M_{Zylinder groß} + M_{Zylinder klein}

Vergleiche deine Lösung: O = 230,91 dm²

V_Körper = V_{Zylinder groß} - V_{Zylinder klein}

Vergleiche deine Lösung: V_Körper = 186,92 dm³

Notiere zunächst die gegebenen und gesuchten Größen!
Erkläre dann die Möglichkeiten, die Oberfläche zu berechnen:
1. Möglichkeit:
O_Körper = O_{Zylinder groß} + M_{Zylinder klein}

2. Möglichkeit:
O_Körper = O_{Zylinder groß} + O_{Zylinder klein} - 2·G_{Zylinder klein}

3. Möglichkeit:

O_Körper = G_{Zylinder unten} + M_{Zylinder unten} + (G_{Zylinder unten} - G_{Zylinder oben}) + M_{Zylinder oben} + G_{Zylinder oben}

V_Körper = V_{Zylinder unten} + V_{Zylinder oben}

Vergleiche deine Lösungen:
3a) Niete A: V≈7945 mm³
Niete B: V≈4819 mm³
b) Niete A: O≈2890 mm²

Niete B: O≈2214 mm²

Erkläre dann die Möglichkeiten, die Oberfläche zu berechnen:
1. Möglichkeit:
O_Körper = O_Zylinder + M_Quader - 2·a·b

2. Möglichkeit:
O_Körper = O_Zylinder + O_Quader - 4·a·b

3. Möglichkeit:

O_Körper = 2·(G_Zylinder - a·b) + M_Zylinder + M_Quader

V_Körper = V_Zylinder - V_Quader

Vergleiche deine Lösungen
V≈873,53 cm³

O≈632,28 cm²

Berechne das Volumen zunächst in der Einheit mm³.
V_Körper = V_Quader - V_{halber Zylinder}

            = V_Quader - $\tfrac{1}{2}$V_Zylinder

Vergleiche deine Lösungen:
a) V=5776,42mm³≈0,0578dm³ (Erinnerung: Die Umwandlungszahl bei Volumina ist 1000.)
1 dm³ wiegt 2,7 kg, also rechne m≈ 0,0578 · 2,7 kg = 0,156kg
b) V≈262,19mm³ ≈0,262cm³

m≈0,707g

Erkläre dann die Möglichkeiten, die Oberfläche zu berechnen:
1. Möglichkeit:
O_Körper = O_{Zylinder links} - G_{Zylinder links} + M_{Zylinder Mitte} + O_{Zylinder rechts} - G_{Zylinder rechts}

Es gibt natürlich auch andere Möglichkeiten.

Vergleiche deine Lösungen:
a) V≈85633,395mm³≈0,085633dm³
m≈0,672kg

b) O≈15780,14mm²