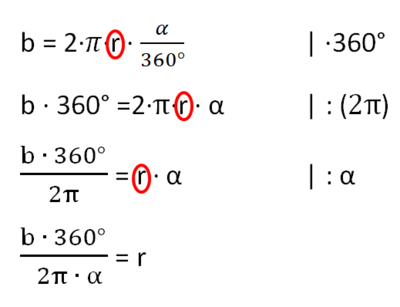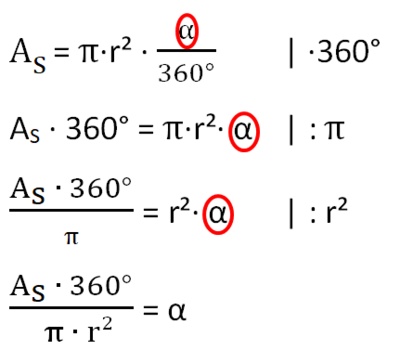Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 122: | Zeile 122: | ||
<ggb_applet id="hgc5mhz3" width="936" height="814" border="888888" /> | <ggb_applet id="hgc5mhz3" width="936" height="814" border="888888" /> | ||
<br> | <br> | ||
===Formeln umstellen=== | |||
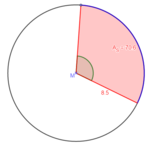
{{Box|1=Formeln umstellen|2=[[Datei:Aufgabe Formel Kreisausschnitt umstellen.png|rechts|rahmenlos|150x150px]] a) geg: A<sub>S</sub> = 38,6 cm²; α = 108°<br> | {{Box|1=Formeln umstellen|2=[[Datei:Aufgabe Formel Kreisausschnitt umstellen.png|rechts|rahmenlos|150x150px]] a) geg: A<sub>S</sub> = 38,6 cm²; α = 108°<br> | ||
ges: r<br> | ges: r<br> | ||
| Zeile 142: | Zeile 146: | ||
{{Lösung versteckt|1=[[Datei:Formel Kreisausschnitt umstellen nach Winkel.png|rahmenlos|400x400px]]|2=Tipp zu c|3=Verbergen}} | {{Lösung versteckt|1=[[Datei:Formel Kreisausschnitt umstellen nach Winkel.png|rahmenlos|400x400px]]|2=Tipp zu c|3=Verbergen}} | ||
{{#ev:youtube|gct3CCDPsH0|800|center|||start=120&end=176}} | {{#ev:youtube|gct3CCDPsH0|800|center|||start=120&end=176}} | ||
Version vom 27. April 2022, 08:24 Uhr
1 Kreisumfang
2 Kreisfläche
3 Kreisteile
4 Zylinder
5 Zusammengesetzte Körper
3 Kreisteile
Welche Arten von Kreisteilen gibt es?
Mache dich mit den verschiedenen Begriffen vertraut:

Applet von GeoGebra Translation Team German, Pöchtrager

3.1 Kreisring
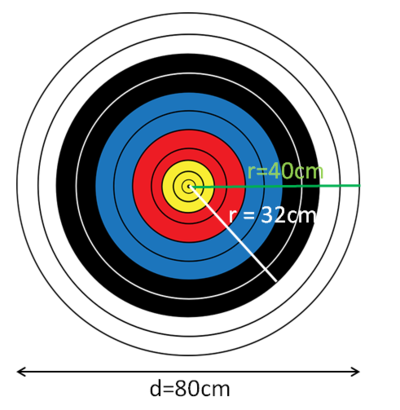
Für die Fläche des weißen Ringes, berechne zunächst den Flächeninhalt der gesamte Scheibe A1 mit dem Radius raußen = 40cm. Subtrahiere anschließend den Flächeninhalt des inneren Kreises A2 mit dem Radius rinnen = 32cm.
AKreisring weiß = A1 - A2
= π·ra² - π·ri²
= π·40² - π·32²
= π·(40² - 32²)
Den Flächeninhalt des schwarzen, blauen und roten Ringes berechne ebenso. Wähle jeweils der Radius des äußeren und inneren Kreises passend:
schwarzer Ring: ra = 32cm; ri = 24cm.
blauer Ring: ra = 24cm; ri = 16cm.
roter Ring: ra = 18cm; ri = 8cm.
Vergleiche deine Lösung zu a)
Aweiß = 1809,56 cm²
Aschwarz = 1407,43 cm²
Ablau = 1005,31 cm²
Arot = 603,19 cm²
Agelb = 201,06 cm²
Für die Berechnungen der Flächeninhalte der Kreisringe hast du immer vom äußeren Kreis den inneren Kreis subtrahiert. Leite so die Formel her:
AKreisring = Aaußen - Ainnen
= π·r²a - π·r²i | π als gleichen Faktor ausklammern
Die Formel wird veranschaulicht im nachfolgenden Applet:

Berechne zunächst r2.
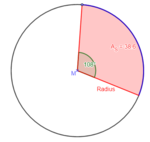
3.2 Kreisausschnitt AS und Kreisbogen b
Beobachte den Zusammenhang zwischen der Fläche des Kreisausschnittes und dem Mittelpunktswinkel α im nachfolgenden Applet:

Applet von IT Wombat
Beispiele:
geg: r = 5cm; α = 72°
Berechne den Flächeninhalt des Kreisausschnittes AS:
AS = π·r²· |Werte einsetzen
= π·5²·
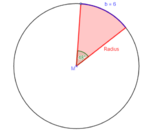
b = 2·π·r· |Werte einsetzen
= 2·π·5·
Prüfe deine Lösungen mithilfe des Applets:

Formeln umstellen
Der Bogen b ist genauso lang wie der Radius r...
1. Idee (leicht): Setzte eine Zahl ein, z.B. b=1, dann ist auch r=1 (b soll genauso lang sein wie r) und stelle die Gleichung nach α um:
b=2·π·r·
1=2·π·1· |·360
360 = 2·π·1·α |:(2·π)
= α
57,3° ≈ α
2. Idee (schwieriger, allgemein): Schreibe die Gleichung mit nur einer Variablen, z.B. r, denn b=r.
b=2·π·r· &nbps; |b=r
r=2·π·r· |·360
r·360 = 2·π·r·α |:(2·π·r)
= α |r kürzen
= α
57,3° ≈ α
b) Gehe ebenso vor, also z.B. b=2, r=1 (b ist doppelt so groß wie r)
oder b = 2r einsetzen
Lösung: α ≈ 114,6°
Gege ebenso vor, also z.B. b=1, r=2 (b ist halb so groß wie r)
oder b=0,5r
Anwendungsaufgaben
Verwende zur Überprüfung deiner Rechnungen das Applet:

Es handelt sich um einen Ausschnitt eines Kreisringes.