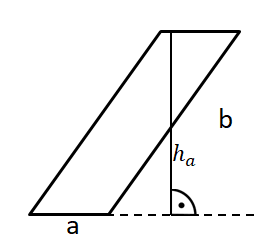Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Parallelogramm: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 6: | Zeile 6: | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen|4.4) Drachen]]<br> | *[[Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Drachen|4.4) Drachen]]<br> | ||
*[[Buss-Haskert/Vierecke und Dreiecke/Bunte Mischung|4.5) Bunte Mischung]]}} | *[[Buss-Haskert/Vierecke und Dreiecke/Bunte Mischung|4.5) Bunte Mischung]]}} | ||
===4.3) Parallelogramm | ===4.3) Parallelogramm=== | ||
====1) Höhe im Parallelogramm==== | |||
Um die Formel für den Flächeninhalt eines Parallelogramms herzuleiten, musst du den Begriff der "Höhe" kennen. | Um die Formel für den Flächeninhalt eines Parallelogramms herzuleiten, musst du den Begriff der "Höhe" kennen. | ||
| Zeile 95: | Zeile 97: | ||
<br> | <br> | ||
<br> | <br> | ||
====2) Formeln herleiten: Flächeninhalt A und Umfang u==== | |||
{{Box|1=Flächeninhalt und Umfang des Parallelogramms|2=[[Datei:Parallelogramm mit zwei Höhen.png|rahmenlos]]<br> | {{Box|1=Flächeninhalt und Umfang des Parallelogramms|2=[[Datei:Parallelogramm mit zwei Höhen.png|rahmenlos]]<br> | ||
| Zeile 119: | Zeile 123: | ||
{{LearningApp|app=pmrr5tk0519|Width=100%|height=600px}} | {{LearningApp|app=pmrr5tk0519|Width=100%|height=600px}} | ||
====3) Formeln umstellen==== | |||
{{Box|Umstellen der Formel|Um die Länge einer Seite oder Höhe zu berechnen, müssen die Formeln für den Flächeninhalt bzw. Umfang umgestellt werden. <br>1. Stelle die Flächeninhaltsformel um nach der Seitenlänge und nach der Länge der Höhe.<br>2. Stelle die Umfangsformel nach einer Seitenlänge um.|Arbeitsmethode}} | {{Box|Umstellen der Formel|Um die Länge einer Seite oder Höhe zu berechnen, müssen die Formeln für den Flächeninhalt bzw. Umfang umgestellt werden. <br>1. Stelle die Flächeninhaltsformel um nach der Seitenlänge und nach der Länge der Höhe.<br>2. Stelle die Umfangsformel nach einer Seitenlänge um.|Arbeitsmethode}} | ||
| Zeile 133: | Zeile 138: | ||
h<sub>a</sub> = <math>\tfrac{A}{a}</math><br></div> | h<sub>a</sub> = <math>\tfrac{A}{a}</math><br></div> | ||
</div> | </div> | ||
Umstellen der Umfangsformel nach einer Seite:<br> | Umstellen der Umfangsformel nach einer Seite:<br> | ||
| Zeile 142: | Zeile 145: | ||
Stelle die Formel entsprechend nach b um. | Stelle die Formel entsprechend nach b um. | ||
{{Box|Übung 4|Löse die nachfolgende LearningApp. Schreibe die Aufgabe struktuiert in deinem Heft mit.|Üben}} | |||
{{LearningApp|app=psp0mexxk19|width=100%|height=600px}} | {{LearningApp|app=psp0mexxk19|width=100%|height=600px}} | ||
<br /> | <br /> | ||
{{Box|Übung | {{Box|Übung 5|Löse Buch | ||
* S. 85 Nr. 7 | * S. 85 Nr. 7 | ||
* S. 96 Nr. 3 | * S. 96 Nr. 3 | ||
Notiere die Formel und stelle sie nach der gesuchten Größe um. Setze dann ein und berechne.|Üben}} | Notiere die Formel und stelle sie nach der gesuchten Größe um. Setze dann ein und berechne.|Üben}} | ||
{{Box|Übung | {{Box|Übung 6|Nachdenkaufgabe: Löse Buch | ||
* S. 86 Nr. 14 | * S. 86 Nr. 14 | ||
Nutze als Hilfe das nachfolgende Applet: Verschiebe den Punkt und beobachte, was mit dem Flächeninhalt und dem Umfang des Parallelogramms geschieht. Notiere und erkläre.|Üben}} | Nutze als Hilfe das nachfolgende Applet: Verschiebe den Punkt und beobachte, was mit dem Flächeninhalt und dem Umfang des Parallelogramms geschieht. Notiere und erkläre.|Üben}} | ||
| Zeile 156: | Zeile 160: | ||
<ggb_applet id="eemvx2an" width="800" height="620" /> | <ggb_applet id="eemvx2an" width="800" height="620" /> | ||
==== 4) Anwendungsaufgaben==== | |||
{{Box|Übung 6: Anwendungsaufgaben zu Parallelogrammen|Löse die Anwendungsaufgaben übersichtlich. Notiere zunächst die gegebenen Größen. Zeichne eine Skizze und beschrifte diese. Überlege, was gesucht ist. Unterscheide zwischen Flächen'''in'''halt A('''in'''nen dr'''in''') und '''Um'''fang u (dr'''um''' her'''um'''). | {{Box|Übung 6: Anwendungsaufgaben zu Parallelogrammen|Löse die Anwendungsaufgaben übersichtlich. Notiere zunächst die gegebenen Größen. Zeichne eine Skizze und beschrifte diese. Überlege, was gesucht ist. Unterscheide zwischen Flächen'''in'''halt A('''in'''nen dr'''in''') und '''Um'''fang u (dr'''um''' her'''um'''). | ||
* S. 86 Nr. 9 | * S. 86 Nr. 9 | ||
| Zeile 162: | Zeile 167: | ||
* S. 86 Nr. 12 | * S. 86 Nr. 12 | ||
* S. 86 Nr. 13|Üben}} | * S. 86 Nr. 13|Üben}} | ||
{{Lösung versteckt|Prüfe, ob die Fläche der Gangway richtig berechnet wurde.|Tipp zu Nr. 9|Verbergen}} | {{Lösung versteckt|Prüfe, ob die Fläche der Gangway richtig berechnet wurde.|Tipp zu Nr. 9|Verbergen}} | ||
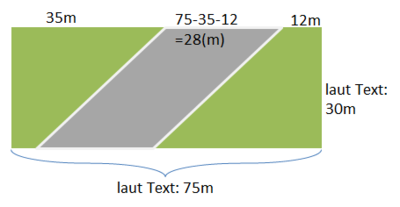
{{Lösung versteckt|Beschrifte die Skizze vollständig und bestimme dann den Flächeninhalt der Straße (Parallelogramm)|Tipp 1 zu Nr. 10|Verbergen}} | {{Lösung versteckt|Beschrifte die Skizze vollständig und bestimme dann den Flächeninhalt der Straße (Parallelogramm)|Tipp 1 zu Nr. 10|Verbergen}} | ||
{{Lösung versteckt|[[Datei:S.86 Nr.10 Tipp.png|rahmenlos|400px]]|Tipp 2 zu Nr. 10|Verbergen}} | {{Lösung versteckt|[[Datei:S.86 Nr.10 Tipp.png|rahmenlos|400px]]|Tipp 2 zu Nr. 10|Verbergen}} | ||
{{Lösung versteckt|1=geg.: Dachfläche zusammengesetzt aus zwei Parallelogrammen mit <br> | {{Lösung versteckt|1=geg.: Dachfläche zusammengesetzt aus zwei Parallelogrammen mit <br> | ||
1. a = 6 m; ha= 4,25m <br> | 1. a = 6 m; ha= 4,25m <br> | ||
Version vom 1. November 2020, 08:29 Uhr
4.3) Parallelogramm
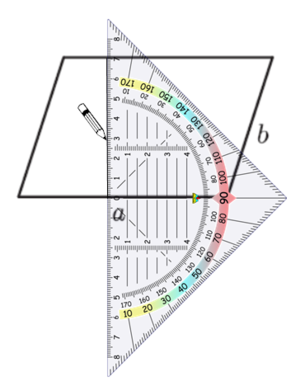
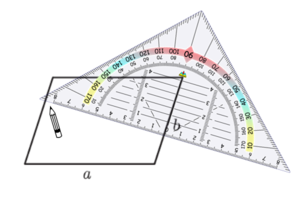
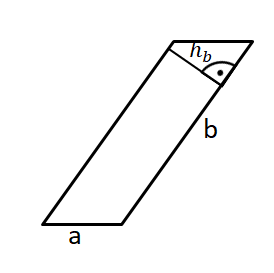
1) Höhe im Parallelogramm
Um die Formel für den Flächeninhalt eines Parallelogramms herzuleiten, musst du den Begriff der "Höhe" kennen.
Verschiebe im nachfolgenden Applet die Punkte und beobachte die Lage der Höhen. Was fällt dir auf?

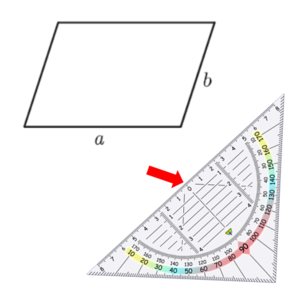
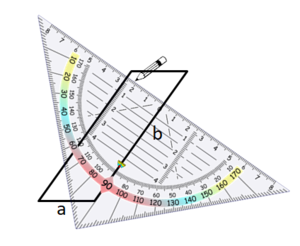
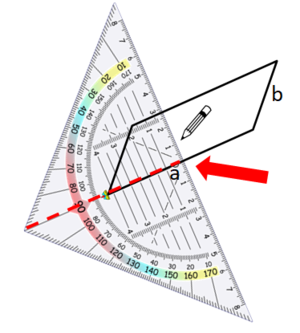
Wiederhole wichtige Begriffe zum Geodreieck: Nullpunkt und Mittellinie
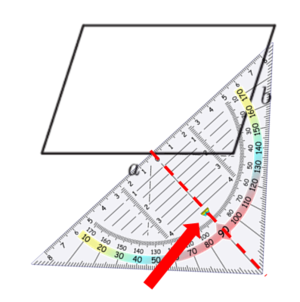
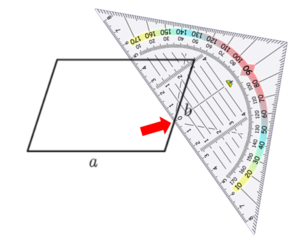
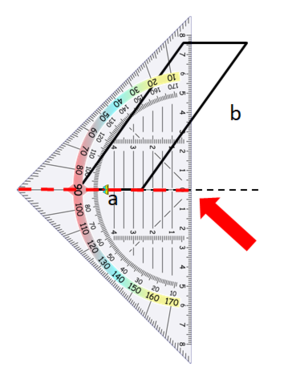
Hier siehst du, wie du Schritt für Schritt die Höhen in das Parallelogramm einzeichnest:
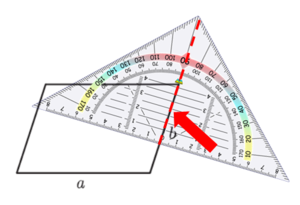
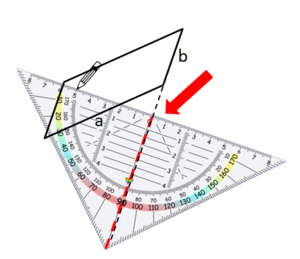
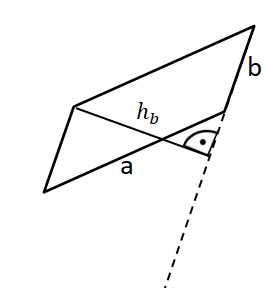
Um die Höhe zur Seite b zu zeichnen, gehe ebenso vor:
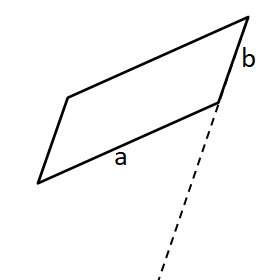
Manchmal musst du die Seiten des Parallelogramms verlängern, um die Höhe zeichnen zu können:
Beispiel 2
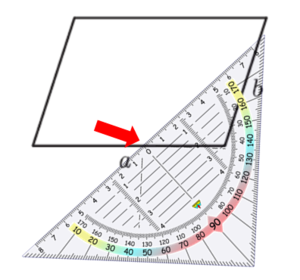
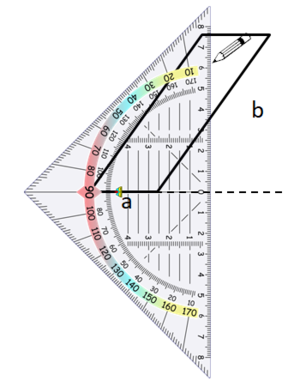
Die Höhe zur Seite b kannst du ohne eine Verlängerung der Seite einzeichnen.
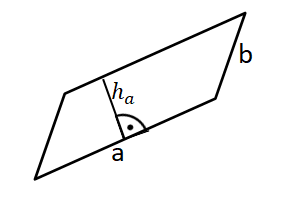
Beispiel 3
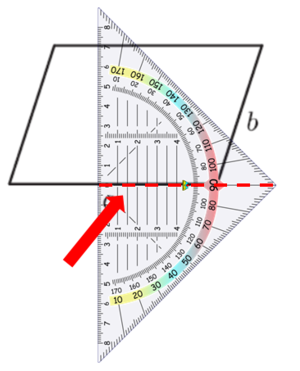
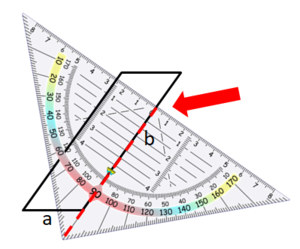
Die Höhe zur Seite a kannst du ohne eine Verlängerung der Seite einzeichnen.

Und nun im Heft...
Nun versuche, mithilfe des GeoGebra-Applets die Formel für den Flächeninhalt des Parallelogramms herzuleiten. Notiere deine Ideen.

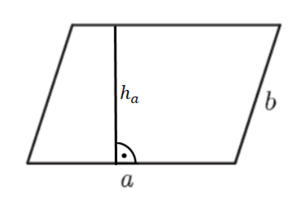
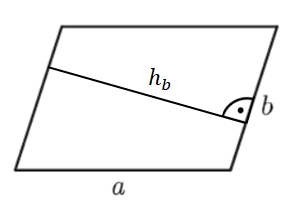
2) Formeln herleiten: Flächeninhalt A und Umfang u

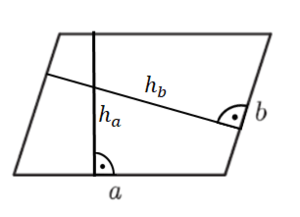
Gegeben sind in der Zeichnung a=8cm; ha=5cm und b=6cm.
A=a∙ha
=8∙5
=40 (cm²) Achte auf die richtige Einheit cm²
=2∙8 + 2∙6
=28 (cm)
Achte auf gleiche Einheiten!
3) Formeln umstellen
A = a∙ha |:ha
= a
a =
A = a∙ha |:a
= ha
Umstellen der Umfangsformel nach einer Seite:
u = 2a + 2b |-2b
u - 2b = 2a |:2 (denn 2a=2∙a, rechne also umgekehrt :2!)
- b = a
Stelle die Formel entsprechend nach b um.

4) Anwendungsaufgaben
geg.: Dachfläche zusammengesetzt aus zwei Parallelogrammen mit
1. a = 6 m; ha= 4,25m
2. a = 4m; ha = 4,25m
35 Dachziegeln pro m²
Hier muss in der Antwort eine sinnvolle Zahl für die gegebene Situation angeben werden!
geg: Treppenaufgang Parallelogramm,
a= 3,30m; ha= 2,00 m
(oder b = 2,7 m ; hb= 2,45 m)
45,30€ pro m²

4.4) Raute: Umfang und Flächeninhalt
Die Raute ist ein besonderes Parallelogramm, also gelten auch die Formeln des Parallelogramms für die Raute.
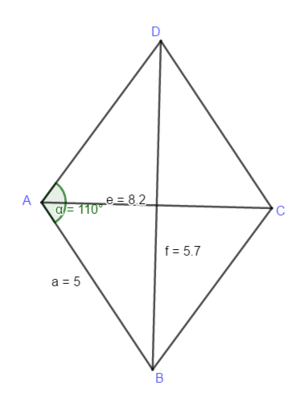
Es gibt eine weitere Möglichkeit, den Flächeninhalt einer Raute zu bestimmen. Bearbeite dazu das Applet. Findest du eine Formel für den Flächeninhalt?

Du kannst deine Rechnung prüfen, wenn du die auch die Höhe einer Seite einzeichnest, misst und dann mit der Flächeninhaltesformel für das Parallelogramm berechnest. Die Flächeninhalte müssen gleich sein.