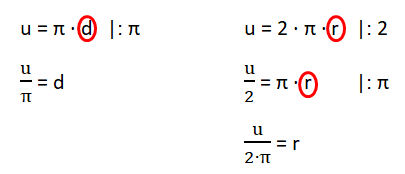Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 270: | Zeile 270: | ||
{{Box|Übung 4 - Sachsituationen|Löse die Aufgabe aus den nachfolgenden GeoGebra-Applets. Notiere die Lösung ausführlich und übersichtlich in deinem Heft. |Üben}} | {{Box|Übung 4 - Sachsituationen|Löse die Aufgabe aus den nachfolgenden GeoGebra-Applets. Notiere die Lösung ausführlich und übersichtlich in deinem Heft. |Üben}} | ||
Originallink https://www.geogebra.org/m/syux7xjs<br> | |||
<ggb_applet id="a5qhbpuf" width="777" height="806" border="888888" /> | |||
<small>Applet von Schober</small><br> | <small>Applet von Schober</small><br> | ||
{{Lösung versteckt|1=Der Weg der Füße entspricht dem Umfang der Erde. Diesen berechnest du mit der Formel u = 2·π·r, wobei der Erdradius r = 6370000m beträgt. <br> | {{Lösung versteckt|1=Der Weg der Füße entspricht dem Umfang der Erde. Diesen berechnest du mit der Formel u = 2·π·r, wobei der Erdradius r = 6370000m beträgt. <br> | ||
| Zeile 284: | Zeile 285: | ||
* S. 130 Nr. 16 (**) | * S. 130 Nr. 16 (**) | ||
* S. 130 Nr. 17 (*)|Üben}} | * S. 130 Nr. 17 (*)|Üben}} | ||
{{Lösung versteckt|Verlgeiche mit Übung 4 (Laufen um die Erde).<br> | {{Lösung versteckt|Verlgeiche mit Übung 4 (Laufen um die Erde). Entnimm den den Erdradius aus der Aufgabe. Berechne den Umfang der Erde und ergänze ihn um 1 m. Wie sehr vergrößert sich dann der Radius?<br> | ||
|Tipp zu Nr. 7|Verbergen}} | |Tipp zu Nr. 7|Verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Originallink https://www.geogebra.org/m/bprvjtx8<br> | |||
<ggb_applet id="bprvjtx8" width="1080" height="790" border="888888" />|2=Tipp 2 zu Nr. 7 (Hilfsapplet)|3=Verbergen}} | <ggb_applet id="bprvjtx8" width="1080" height="790" border="888888" />|2=Tipp 2 zu Nr. 7 (Hilfsapplet)|3=Verbergen}} | ||
{{Lösung versteckt|Vergleiche mit der Einstiegsaufgabe.|Tipp zu Nr. 11|Verbergen}} | {{Lösung versteckt|Vergleiche mit der Einstiegsaufgabe.|Tipp zu Nr. 11|Verbergen}} | ||
Aktuelle Version vom 22. März 2024, 17:17 Uhr
1 Kreisumfang
2 Kreisfläche
3 Kreisteile
4 Zylinder
5 Zusammengesetzte Körper
1 Kreisumfang u
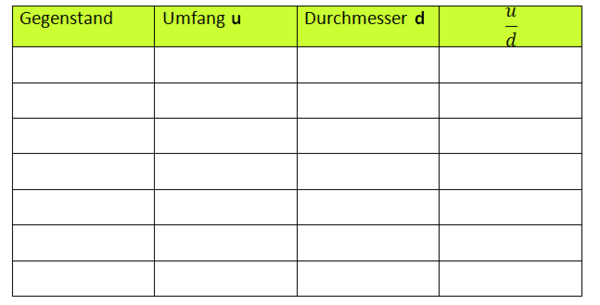
1.1 Kreisumfang entdecken
Prüfe deine Vermutung aus dem Teil c) mithilfe des nachfolgenden Applets. Wähle den Vollbildmodus zur Bearbeitung.
Applet von Pöchtrager
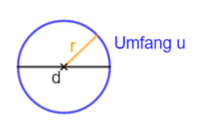
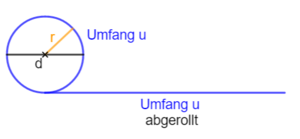
Der Umfang u eines Kreises ist proportional zu seinem Durchmesser d.
Der Quotient beträgt immer ca. 3,1.
Zusammenfassung:
1.2 Exkurs: Kreiszahl π
Beim Kreis ist das Verhältnis von Umfang u und Durchmesser d ist immer gleich.
Dieses Verhältnis wird Kreiszahl π genannt. = π = 3,141... Dieser Dezimalbruch endet nie.
Dorfuchs hat die ersten 200 Nachkommastellen von π mit einer Fußballjonglage verbunden: Beeindruckend!
Wir nähern uns Durfuchs an: 😉
Das folgende Näherungsverfahren für die Kreiszahl π geht auf Archimedes (282 v.Chr. Bis 212 v.Chr.) zurück. Es beruht auf der Betrachtung von regelmäßigen Vielecken, die dem Kreis umschrieben bzw. einbeschrieben sind.

Applet von Pöchtrager
Und nun noch einige kurze Infos zur Kreiszahl π:
- eine der bekanntesten und sagenumwobensten Zahlen der Mathematik
- Ansätze ihrer Berechnung wurden schon im 17 Jahrhundert v. Chr. im Rechenbuch des Ahmes angedeutet
- mathematisch relativ genau als erstes von dem griechischen Mathematiker und Philosoph Archimedes im Jahr 250 v .Chr. bestimmt worden, mit 2 Dezimalstellen (3,14)
- Mittlerweile (2010) von dem Mathematiker Shigero Kondo auf ca. 5 000 000 000 000 Dezimalstellen berechnet
- beschreibt das Verhältnis vom Umfang des Kreise zu seinem Durchmesser, welches bei allen Kreisen gleich ist:
π = = 3,14159...
- Ein Kreis mit dem Durchmesser 1 hat somit einen Umfang von π.
Tastenkombination für die Kreiszahl π für Berechnungen mit dem Taschenrechner:

1.3 Kreisumfang - Berechnungen
Beispiele:
geg: d = 3,0 cm
ges: u
u = π · d |Wert einsetzen
= π · 3,0
geg: r = 1,0 cm
ges: u
u = 2 · π · r |Wert einsetzen
= 2 · π · 1,0
geg: u = 15,7 cm
ges: d
u = π · d |: π
= d |Wert einsetzen
= d
geg: u = 22,0 cm
ges: r
u = 2 · π · r |: (2·π)
= r Wert einsetzen
= r
Prüfe deine Lösungen mit dem Applet:

Applet von C. Buß-Haskert
Formel: Durchmesser mal 3 plus 5%:
Für d = 40 cm:
"Durchmesser mal 3" 40·3 = 120 (cm)
"plus 5%" 5% von 120 = 6 (cm) (Rechne mit Formel oder mit Dreisatz)
geg: G=120cm; p%=5%=0,05
ges: W
| Prozentsatz p% | Strecke (cm) |
|---|---|
| 100% | 120 |
| 10% | 12 |
| 5% | 6 |
Die Formel für den Umfang lautet u = π·d.
In der Faustformel wird gerechnet:
u = 3·d + 0,05·(3·d) (Durchmesser mal 3 plus 5%)
= 3·d + 0,15·d
= 3,15·d
1.4 Anwendungsaufgaben
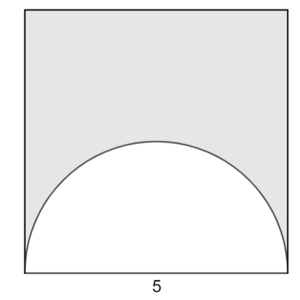
- Der Umfang zweier Halbkreise ist genauso groß wie der Umfang eines ganzen Kreises (bei gleichem Radius).
Laufe die drei Strecken des Rechtecks und dann die zwei Halbkreise entlang ("die Ameise läuft drum herum")
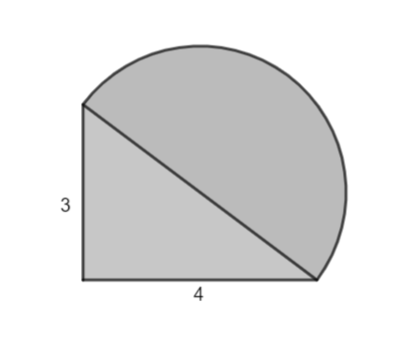
Berechne den Durchmesser d des Halbkreises mit dem Satz des Pythagoras.
In jedem rechtwinkligen Dreieck gilt:
Kathete2 + Kathete2 = Hypotenuse2
Der Umfang des Halbreises ist halb so groß wie der eines Kreises:
uHalbreis = uKreis = π·d
Hilfsapplet zu Nr. 5

Betrachte den Durchmesser der Kreise. Was geschieht jeweils von Bogen zu Bogen?
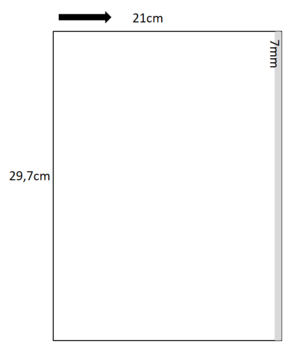
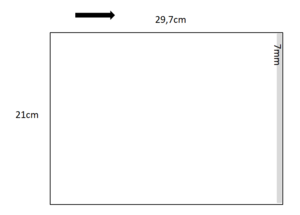
d1=2cm; d2=1cm; d3=; d4=; d5 = ; ...
geg: u1 = 21-0,7 = 20,3 (cm) u2 = 29,7 - 0,7 = 29 (cm)
ges: d
Originallink https://www.geogebra.org/m/syux7xjs

Applet von Schober
Der Weg der Füße entspricht dem Umfang der Erde. Diesen berechnest du mit der Formel u = 2·π·r, wobei der Erdradius r = 6370000m beträgt.
Verlgeiche mit Übung 4 (Laufen um die Erde). Entnimm den den Erdradius aus der Aufgabe. Berechne den Umfang der Erde und ergänze ihn um 1 m. Wie sehr vergrößert sich dann der Radius?
Originallink https://www.geogebra.org/m/bprvjtx8

Die Länge des Metallbandes entspricht dem Umfang des entstehenden Kreises.
Gesucht ist der Weg, den das Rad an einem Tag zurücklegt.
d=Höhe des Rads = 1,95. Berechne u.
Weg des Rads an einem Tag: 6000·u, da sich das Rad 6000 mal dreht.
Eine Umdrehung des Rades entsprich dem Umfang des Rades. 2 Umdrehungen sind also gleich 2·u.
Stelle eine Gleichung auf und löse diese nach d auf.
Gleiche Einheiten! Wandle die Geschwindigkeit von 25 km/h in die Einheit cm/s um.
Berechne den Umfang des Dynamorädchens.
Berechne danach, wie oft dieser Umfang in 694,4 cm (so weit dreht sich das Rad pro Sekunde) passt.
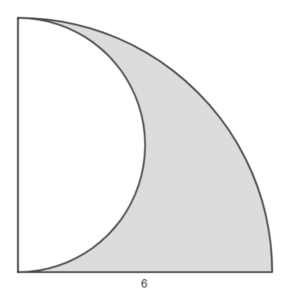
Wie viele "Wellen" befinden sich in der Wellblechplatte?
2,50m Länge = 250cm (gleiche Einheiten!)
250cm : 5cm = 50
Ursprünglich muss die Platte so lang gewesen sein, dass 50 Wellen daraus zu legen sind:
Länge ursprünglich = 50·Umfang eines Halbkreises mit d=5cm
= 25·Umfang eines ganzen Kreises mit d=5cm.
Länge = 25·π·d=...
Berechne den Umfang u des Kraters mit d=24km.
Teile diese Strecke auf drei Tage auf.
- ↑ nach einer Idee von Schober auf GeoGebra https://www.geogebra.org/m/hh7dahad#material/ybzhmw8f