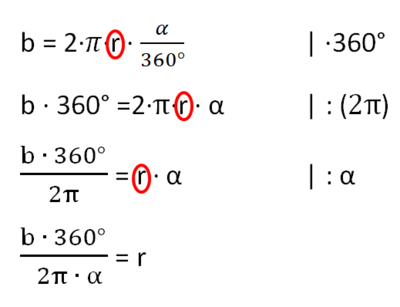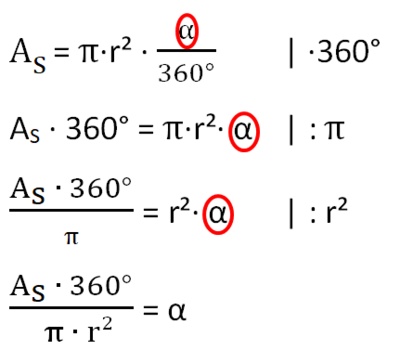Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile: Unterschied zwischen den Versionen
(Tipps) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (57 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
<br> | <br> | ||
{{Navigation|[[Benutzer:Buss-Haskert/Kreis und Zylinder|Kreis und Zylinder - Startseite]]<br> | {{Navigation|[[Benutzer:Buss-Haskert/Kreis und Zylinder|Kreis und Zylinder - Startseite]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang|1 Kreisumfang]]<br> | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang|1 Kreisumfang]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisfläche|2 Kreisfläche]]<br> | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisfläche|2 Kreisfläche]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile|3 Kreisteile]] | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile|3 Kreisteile]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Zylinder|4 Zylinder]]<br> | |||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Zusammengesetzte Körper|5 Zusammengesetzte Körper]] | |||
}} | }} | ||
== 3 Kreisteile == | <br> | ||
==3 Kreisteile== | |||
Welche Arten von Kreisteilen gibt es?<br> | Welche Arten von Kreisteilen gibt es?<br> | ||
| Zeile 14: | Zeile 17: | ||
Applet von GeoGebra Translation Team German, Pöchtrager<br> | Applet von GeoGebra Translation Team German, Pöchtrager<br> | ||
=== 3.1 Kreisring === | {{Box|Übung 1 - Begriffe|Bearbeite die nachfolgenden Apps (Autor: FLINK-Team, GeoGebra)|Üben}} | ||
{{LearningApp|app=ph5k4j3kj21|width=100%|height=600px}} | |||
<ggb_applet id="vfesfj5z" width="800" height="640" border="888888" /> | |||
===3.1 Kreisring=== | |||
{{Box|1=Kreisringe - Bogenschießen|2=[[Datei:Target-459833 1920.jpg|rechts|rahmenlos|150x150px]][[Datei:Archery-152912 1280.png|rechts|rahmenlos|150x150px]]Die Scheibe beim Bogenschießen besteht aus Kreisringen mit fünf verschiedenen Farben, wobei jeder Farbring gleich breit ist. Der Durchmesser der Bogenscheibe beträgt 80 cm. Die Punkte werden danach verteilt, welcher Ring getroffen wird. <br> | {{Box|1=Kreisringe - Bogenschießen|2=[[Datei:Target-459833 1920.jpg|rechts|rahmenlos|150x150px]][[Datei:Archery-152912 1280.png|rechts|rahmenlos|150x150px]]Die Scheibe beim Bogenschießen besteht aus Kreisringen mit fünf verschiedenen Farben, wobei jeder Farbring gleich breit ist. Der Durchmesser der Bogenscheibe beträgt 80 cm. Die Punkte werden danach verteilt, welcher Ring getroffen wird. <br> | ||
| Zeile 21: | Zeile 29: | ||
b) Leite eine Formel herleiten, mit der du den Flächeninhalt von Kreisringen bestimmen kannst.|3=Unterrichtsidee}} | b) Leite eine Formel herleiten, mit der du den Flächeninhalt von Kreisringen bestimmen kannst.|3=Unterrichtsidee}} | ||
{{Lösung versteckt|1=[[Datei:Scheibe Bogenschießen.png|rahmenlos|410x410px]]<br> | {{Lösung versteckt|1=[[Datei:Scheibe Bogenschießen.png|rahmenlos|410x410px]]<br> | ||
Für die Fläche des weißen Ringes, berechne zunächst den Flächeninhalt der gesamte Scheibe A<sub>1</sub> mit dem Radius r<sub>außen</sub> = 40cm. Subtrahiere anschließend den Flächeninhalt des inneren Kreises A<sub>2</sub> mit dem Radius r<sub>innen</sub>. <br>|2=Tipp 1|3=Verbergen}} | Für die Fläche des weißen Ringes, berechne zunächst den Flächeninhalt der gesamte Scheibe A<sub>1</sub> mit dem Radius r<sub>außen</sub> = 40cm. Subtrahiere anschließend den Flächeninhalt des inneren Kreises A<sub>2</sub> mit dem Radius r<sub>innen</sub> = 32cm. <br> | ||
Jeder Kreisring ist 8 cm breit.|2=Tipp 1|3=Verbergen}} | |||
{{Lösung versteckt|1=A<sub>Kreisring weiß</sub> = A<sub>1</sub> - A<sub>2</sub> <br> | {{Lösung versteckt|1=A<sub>Kreisring weiß</sub> = A<sub>1</sub> - A<sub>2</sub> <br> | ||
= π·r<sub>a</sub>² - π·r<sub>i</sub>²<br> | = π·r<sub>a</sub>² - π·r<sub>i</sub>²<br> | ||
| Zeile 27: | Zeile 36: | ||
= π·(40² - 32²) | = π·(40² - 32²) | ||
= 1809,56 (cm²)|2=Tipp 2|3=Verbergen}} | = 1809,56 (cm²)|2=Tipp 2|3=Verbergen}} | ||
{{Lösung versteckt|1=Den Flächeninhalt des schwarzen, blauen und roten Ringes berechne ebenso. Wähle jeweils der Radius des äußeren und inneren Kreises passend:<br> | |||
schwarzer Ring: r<sub>a</sub> = 32cm; r<sub>i</sub> = 24cm.<br> | |||
blauer Ring: r<sub>a</sub> = 24cm; r<sub>i</sub> = 16cm.<br> | |||
roter Ring: r<sub>a</sub> = 16cm; r<sub>i</sub> = 8cm.<br> | |||
Der gelbe Kreis ist ein ganzer Kreis mit dem Radius r = 8cm.|2=Tipp 3|3=Verbergen}} | |||
{{Lösung versteckt|1=Vergleiche deine Lösung zu a)<br> | |||
A<sub>weiß</sub> = 1809,56 cm²<br> | |||
A<sub>schwarz</sub> = 1407,43 cm²<br> | |||
A<sub>blau</sub> = 1005,31 cm²<br> | |||
A<sub>rot</sub> = 603,19 cm²<br> | |||
A<sub>gelb</sub> = 201,06 cm²<br> | |||
Da der Flächeninhalt immer kleiner wird, ist es sinnvoll für eine kleiner Fläche mehr Punkte zu verteilen.|2=Vergleiche deine Lösungen zu a|3=Verbergen}} | |||
{{Lösung versteckt|1=Für die Berechnungen der Flächeninhalte der Kreisringe hast du immer vom äußeren Kreis den inneren Kreis subtrahiert. Leite so die Formel her:<br> | |||
A<sub>Kreisring</sub> = A<sub>außen</sub> - A<sub>innen</sub><br> | |||
= π·r²<sub>a</sub> - π·r²<sub>i</sub> | π als gleichen Faktor ausklammern<br> | |||
= π·(r²<sub>a</sub> - r²<sub>i</sub>)|2=Tipp zu b|3=Verbergen}} | |||
{{Box|1=Kreisring|2=Flächeninhalt eines Kreisringes:<br> | |||
A<sub>Kreisring</sub> = π·r<sub>a</sub>² - π·r<sub>i</sub>² | (π als gleichen Faktor ausklammern)<br> | |||
= π·(r²<sub>a</sub> - r²<sub>i</sub>)|3=Arbeitsmethode}}<br> | |||
Die Formel wird veranschaulicht im nachfolgenden Applet: https://www.geogebra.org/m/mdksvgq6<br> | |||
<ggb_applet id="mdksvgq6" width="1074" height="814" border="888888" /> | |||
{{#ev:youtube|vbJME9wVAGU|800|center}} | |||
<br> | |||
{{Box|Übung 2|Löse die Aufgabe aus dem Buch und prüfe deine Ergebnisse mit dem Applet oben. | |||
* S. 150 Nr. 6|Üben}} | |||
{{Lösung versteckt|1=Berechne zunächst r<sub>2</sub>.<br> | |||
r<sub>2</sub>=r<sub>1</sub>+a|2=Tipp zu Nr. 6b|3=Verbergen}} | |||
{{Box|Übung 3|Löse auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/kreis/kreisflaeche.shtml '''Aufgabenfuchs'''] die Aufgaben | |||
* 5 | |||
* 23 (Profi-Aufgabe, freiwillig)|Üben}} | |||
{{Lösung versteckt|1=gegeben: A Kreisring und d, also auch der äußere Radius r<sub>a</sub>.<br> | |||
Stelle die Gleichung für den Flächeninhalt des Kreisringes nach <sub>i</sub> um:<br> | |||
A = π·<math>r_a^2</math> - π·<math>r_i^2</math> |+π·<math>r_i^2</math><br> | |||
π·<math>r_i^2</math> + A = π·<math>r_a^2</math> |-A<br> | |||
π·<math>r_i^2</math> = π·<math>r_a^2</math> - A |:π<br> | |||
<math>r_i^2</math> = <math>\tfrac{\pi \cdot r_a^2 - A}{\pi}</math> |<math>\surd</math><br> | |||
<math>r_i^2</math> = <math>\sqrt{\tfrac{\pi \cdot r_a^2 - A}{\pi}}</math> |Werte einsetzen<br> | |||
<math>r_i</math> = ...|2=Formel umstellen Nr. 23|3=Verbergen}} | |||
{{Box|Übung 4 - Anwendung|Löse die nachfolgenden LearningApps.|Üben}} | |||
{{LearningApp|app=ppwg6p33j21|width=100%|height=600px}} | |||
{{LearningApp|app=pnpgfj31a21|width=100%|heigth=600px}} | |||
<br> | |||
===3.2 Kreisausschnitt A<sub>S</sub> und Kreisbogen b=== | |||
{{Box|Kreisteile - Begriffe|Teile einen Kreis durch zwei Radien.<br> | |||
[[Datei:Kreisteile Begriffe.png|rahmenlos|800x800px]]|Kurzinfo}} | |||
{{LearningApp|app=pa27foggc19|width=100%|height=500px}} | |||
<br> | |||
Beobachte den Zusammenhang zwischen der Fläche des Kreisausschnittes und dem Mittelpunktswinkel α im nachfolgenden Applet: | |||
<ggb_applet id="b5y4nywx" width="700" height="500" border="888888" /> | <ggb_applet id="b5y4nywx" width="700" height="500" border="888888" /> | ||
Applet von IT Wombat | Applet von IT Wombat | ||
<br> | <br> | ||
<br> | <br> | ||
{{Box|Übung 5|Löse die folgende LearningApp zu Mittelpunktswinkeln und ihren Bezeichnungen|Üben}} | |||
{{LearningApp|app=p3o29ay9n20|width=100%|heigth=600px}} | {{LearningApp|app=p3o29ay9n20|width=100%|heigth=600px}} | ||
{{#ev:youtube|vMCZV8bbdE8|800|center}} | {{Box|1=Kreisausschnitt und Kreisbogen|2=Übertrage den Hefteintrag und die Beispiele in dein Heft.<br>[[Datei:Hefteintrag Kreisteile.png|rahmenlos|800x800px]]|3=Arbeitsmethode}} | ||
Beispiele:<br> | |||
geg: r = 5cm; α = 72°<br> | |||
<div class="grid"> | |||
<div class="width-1-2"> | |||
Berechne den Flächeninhalt des Kreisausschnittes A<sub>S</sub>:<br> | |||
A<sub>S</sub> = π·r²·<math>\tfrac{\alpha}{360^\circ}</math> |Werte einsetzen<br> | |||
= π·5²·<math>\tfrac{72^\circ}{360^\circ}</math><br> | |||
= 15,71 (cm²)<br></div> | |||
<div class="width-1-2">Berechne die Länge des Kreisbogens b:<br> | |||
b = 2·π·r·<math>\tfrac{\alpha}{360^\circ}</math> |Werte einsetzen<br> | |||
= 2·π·5·<math>\tfrac{72^\circ}{360^\circ}</math><br> | |||
= 6,3 (cm)<br></div> | |||
</div> | |||
{{Box|Übung 6|Löse auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/kreis/teilkreis.shtml '''Aufgabenfuchs'''] die Aufgaben | |||
* 1 | |||
* 2 | |||
* 3 | |||
* 4 | |||
* 5|Üben}} | |||
<br> | |||
<div class="grid"> | |||
<div class="width-1-2">{{#ev:youtube|vMCZV8bbdE8|460|center}}</div> | |||
<div class="width-1-2">{{#ev:youtube|gct3CCDPsH0|460|center}}</div> | |||
</div> | |||
<br> | |||
{{Box|Übung 7|Löse die Aufgaben aus dem Buch. Achte auf eine ausführliche und übersichtliche Darstellung. | |||
* S. 138 Nr. 2 | |||
* S. 138 Nr. 3|Üben}} | |||
Prüfe deine Lösungen mithilfe des Applets: | |||
<ggb_applet id="hgc5mhz3" width="936" height="814" border="888888" /> | |||
<br> | |||
===Formeln umstellen=== | |||
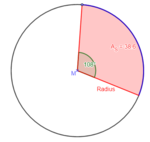
{{Box|1=Formeln umstellen|2=[[Datei:Aufgabe Formel Kreisausschnitt umstellen.png|rechts|rahmenlos|150x150px]] a) geg: A<sub>S</sub> = 38,6 cm²; α = 108°<br> | |||
ges: r<br> | |||
<br> | |||
<br> | |||
<br> | |||
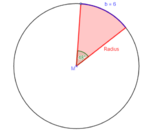
[[Datei:Aufgabe Formel Kreisbogen umstellen.png|rechts|rahmenlos|150x150px]] b) geg: b = 6cm; α = 48°<br> | |||
ges: r <br> | |||
<br> | |||
<br> | |||
<br> | |||
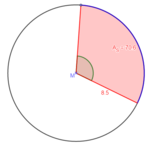
[[Datei:Formel umstellen Kreisausschnitt nach Winkel.png|rechts|rahmenlos|150x150px]] c) geg: r = 8,5 cm; A<sub>S</sub> = 70,6 cm²<br> | |||
ges: α<br> | |||
<br> | |||
<br> | |||
<br> | |||
Stelle jeweils die Formeln nach der gesuchten Größe um. Prüfe deine Lösungen mithilfe des obigen Applets.|3=Unterrichtsidee}} | |||
{{Lösung versteckt|1=[[Datei:Formel Kreisausschnitt umstellen nach r.png|rahmenlos|467x467px]]|2=Tipp zu a|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:Formel Kreisbogen umstellen nach r.png|rahmenlos|400x400px]]|2=Tipp zu b|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:Formel Kreisausschnitt umstellen nach Winkel.png|rahmenlos|400x400px]]|2=Tipp zu c|3=Verbergen}} | |||
{{#ev:youtube|gct3CCDPsH0|800|center|||start=120&end=176}} | |||
{{Box|Übung 8|Löse die Aufgaben aus dem Buch. Stelle dazu die entsprechenden Formeln nach der gesuchten Größe um. Prüfe deine Lösung mit dem Applet oben. | |||
* S. 138 Nr. 4 b,c | |||
* S. 138 Nr. 5 a,c | |||
* S. 138 Nr. 6 | |||
* S. 138 Nr. 7 (Wähle hier die Übungen aus, bei denen du noch Schwierigkeiten in Nr. 4 bzw. Nr. 5 hattest.)|Üben}} | |||
{{Lösung versteckt|1=geg: b und r<br> | |||
ges: α<br> | |||
Stelle die Kreisbogen-Formel nach α um:<br> | |||
b = 2πr·<math>\tfrac{\alpha}{360}</math> |·360 ("Nenner weg")<br> | |||
360°·b = 2πr·α | : (2πr)<br> | |||
<math>\tfrac{360 \cdot b}{2\pi r}</math> = α | Werte einsetzen<br> | |||
... |2=Tipp zu Nr. 5a (Formel umstellen)|3=Verbergen}} | |||
{{Lösung versteckt|1=Lösungen:<br> | |||
4b) r ≈ 1,11 cm; 4c) r ≈ 20,0 cm<br> | |||
5a) α ≈ 80,21°; 5c) α ≈ 144,3°|2=Vergleiche deine Lösungen zu Nr. 4 und 5|3=Verbergen}} | |||
{{Lösung versteckt|1=Der Bogen b ist genauso lang wie der Radius r...<br> | |||
1. Idee (leicht): Setzte eine Zahl ein, z.B. b=1, dann ist auch r=1 (b soll genauso lang sein wie r) und stelle die Gleichung nach α um:<br> | |||
b=2·π·r·<math>\tfrac{\alpha}{360}</math><br> | |||
1=2·π·1·<math>\tfrac{\alpha}{360}</math> |·360<br> | |||
360 = 2·π·1·α |:(2·π)<br> | |||
<math>\tfrac{360}{2\pi}</math> = α<br> | |||
57,3° ≈ α<br> | |||
<br> | |||
2. Idee (schwieriger, allgemein): Schreibe die Gleichung mit nur einer Variablen, z.B. r, denn b=r.<br> | |||
b=2·π·r·<math>\tfrac{\alpha}{360}</math> &nbps; |b=r<br> | |||
r=2·π·r·<math>\tfrac{\alpha}{360}</math> |·360<br> | |||
r·360 = 2·π·r·α |:(2·π·r)<br> | |||
<math>\tfrac{360}{2\pi r}</math> = α |r kürzen <br> | |||
<math>\tfrac{360}{2\pi}</math> = α<br> | |||
57,3° ≈ α<br> | |||
<br> | |||
b) Gehe ebenso vor, also z.B. b=2, r=1 (b ist doppelt so groß wie r)<br> | |||
oder b = 2r einsetzen<br> | |||
Lösung: α ≈ 114,6°<br> | |||
Gege ebenso vor, also z.B. b=1, r=2 (b ist halb so groß wie r)<br> | |||
oder b=0,5r<br> | |||
α ≈ 28,6°<br>|2=Tipp zu Nr. 6|3=Verbergen}} | |||
===Anwendungsaufgaben=== | |||
{{Box|Übung 9 - Anwendungen|Löse die Aufgabe aus dem Buch und die Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/kreis/kreis.shtml '''Aufgabenfuchs'''] | |||
* S. 138 Nr. 8 | |||
* 12 | |||
* 13 | |||
* 39 | |||
* 42 | |||
* 43|Üben}} | |||
{{Lösung versteckt|1=Du findest im Aufgabentext Informationen zum Radius und zum Mittelpunktswinkel. |2=Tipp zu Nr. 8|3=Verbergen}} | |||
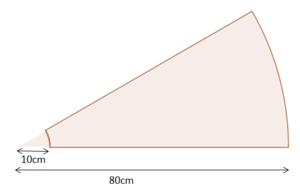
{{Box|Übung 10 - Profiaufgaben|[[Datei:Scheibenwischeraufgabe.png|rechts|rahmenlos|300x300px]]* Scheibenwischer<br> | |||
Der Scheibenwischer eines Autos hat eine Länge von 48cm. Vom Drehpunkt bis zum unteren Ende des Wischerblattes sind es 16cm. Der Scheibenwischer schwenkt über einen Winkel von 150° hin und her. Berechne den Flächeninhalt der erfassten Fläche. | |||
<br> | |||
<br> | |||
<br> | |||
[[Datei:Wendeltreppe Stufe.png|rechts|rahmenlos|300x300px]]* Wendeltreppe<br> | |||
Eine Wendeltreppe besteht aus 12 Stufen, die zusammen eine vollständige Drehung ergeben. Die Stufen einer Wendeltreppe haben die im Bild angegebenen Maße. Bestimme den Flächeninhalt einer Treppenstufe.|Üben}} | |||
{{Lösung versteckt|1=Verwende zur Überprüfung deiner Rechnungen das Applet:<br>Originallink: https://www.geogebra.org/m/ruaau9qb<br> | |||
<ggb_applet id="ruaau9qb" width="1904" height="948" border="888888" /><br>|2=Tipp Animation|3=Verbergen}} | |||
{{Lösung versteckt|1=Es handelt sich um einen Ausschnitt eines Kreisringes.<br> | |||
A = A<sub>Kreisring</sub> · <math>\tfrac{\alpha}{360^\circ}</math>|2=Tipp zur Rechnung|3=Verbergen}} | |||
{{Lösung versteckt|1=Der Mittelpunktswinkel α beträgt 360°:12 = 30°, da 12 Stufen genau 360° ergeben.|2=Tipp zur Aufgabe Wendeltreppe|3=Verbergen}} | |||
===Zusammenfassung=== | |||
{{#ev:youtube|_qjewJyQCJo|800|center}} | |||
{{Fortsetzung|weiter=4 Zylinder|weiterlink=Benutzer:Buss-Haskert/Kreis und Zylinder/Zylinder}} | |||
Aktuelle Version vom 19. April 2024, 14:28 Uhr
1 Kreisumfang
2 Kreisfläche
3 Kreisteile
4 Zylinder
5 Zusammengesetzte Körper
3 Kreisteile
Welche Arten von Kreisteilen gibt es?
Mache dich mit den verschiedenen Begriffen vertraut:

Applet von GeoGebra Translation Team German, Pöchtrager

3.1 Kreisring
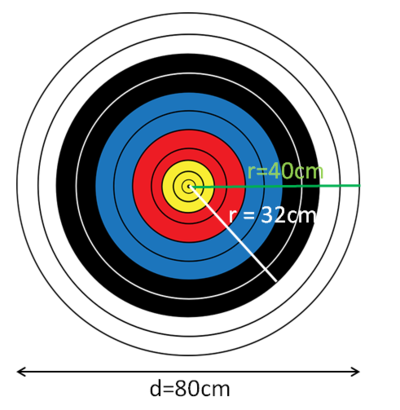
Für die Fläche des weißen Ringes, berechne zunächst den Flächeninhalt der gesamte Scheibe A1 mit dem Radius raußen = 40cm. Subtrahiere anschließend den Flächeninhalt des inneren Kreises A2 mit dem Radius rinnen = 32cm.
AKreisring weiß = A1 - A2
= π·ra² - π·ri²
= π·40² - π·32²
= π·(40² - 32²)
Den Flächeninhalt des schwarzen, blauen und roten Ringes berechne ebenso. Wähle jeweils der Radius des äußeren und inneren Kreises passend:
schwarzer Ring: ra = 32cm; ri = 24cm.
blauer Ring: ra = 24cm; ri = 16cm.
roter Ring: ra = 16cm; ri = 8cm.
Vergleiche deine Lösung zu a)
Aweiß = 1809,56 cm²
Aschwarz = 1407,43 cm²
Ablau = 1005,31 cm²
Arot = 603,19 cm²
Agelb = 201,06 cm²
Für die Berechnungen der Flächeninhalte der Kreisringe hast du immer vom äußeren Kreis den inneren Kreis subtrahiert. Leite so die Formel her:
AKreisring = Aaußen - Ainnen
= π·r²a - π·r²i | π als gleichen Faktor ausklammern
Die Formel wird veranschaulicht im nachfolgenden Applet: https://www.geogebra.org/m/mdksvgq6

Berechne zunächst r2.
gegeben: A Kreisring und d, also auch der äußere Radius ra.
Stelle die Gleichung für den Flächeninhalt des Kreisringes nach i um:
A = π· - π· |+π·
π· + A = π· |-A
π· = π· - A |:π
= |
= |Werte einsetzen
3.2 Kreisausschnitt AS und Kreisbogen b
Beobachte den Zusammenhang zwischen der Fläche des Kreisausschnittes und dem Mittelpunktswinkel α im nachfolgenden Applet:

Applet von IT Wombat
Beispiele:
geg: r = 5cm; α = 72°
Berechne den Flächeninhalt des Kreisausschnittes AS:
AS = π·r²· |Werte einsetzen
= π·5²·
b = 2·π·r· |Werte einsetzen
= 2·π·5·
Prüfe deine Lösungen mithilfe des Applets:

Formeln umstellen
geg: b und r
ges: α
Stelle die Kreisbogen-Formel nach α um:
b = 2πr· |·360 ("Nenner weg")
360°·b = 2πr·α | : (2πr)
= α | Werte einsetzen
Lösungen:
4b) r ≈ 1,11 cm; 4c) r ≈ 20,0 cm
Der Bogen b ist genauso lang wie der Radius r...
1. Idee (leicht): Setzte eine Zahl ein, z.B. b=1, dann ist auch r=1 (b soll genauso lang sein wie r) und stelle die Gleichung nach α um:
b=2·π·r·
1=2·π·1· |·360
360 = 2·π·1·α |:(2·π)
= α
57,3° ≈ α
2. Idee (schwieriger, allgemein): Schreibe die Gleichung mit nur einer Variablen, z.B. r, denn b=r.
b=2·π·r· &nbps; |b=r
r=2·π·r· |·360
r·360 = 2·π·r·α |:(2·π·r)
= α |r kürzen
= α
57,3° ≈ α
b) Gehe ebenso vor, also z.B. b=2, r=1 (b ist doppelt so groß wie r)
oder b = 2r einsetzen
Lösung: α ≈ 114,6°
Gege ebenso vor, also z.B. b=1, r=2 (b ist halb so groß wie r)
oder b=0,5r
Anwendungsaufgaben
Verwende zur Überprüfung deiner Rechnungen das Applet:
Originallink: https://www.geogebra.org/m/ruaau9qb

Es handelt sich um einen Ausschnitt eines Kreisringes.