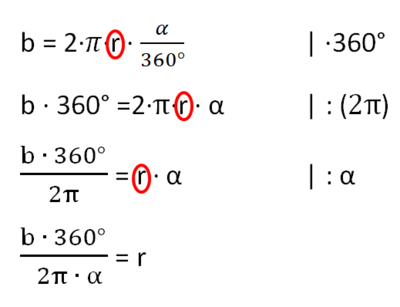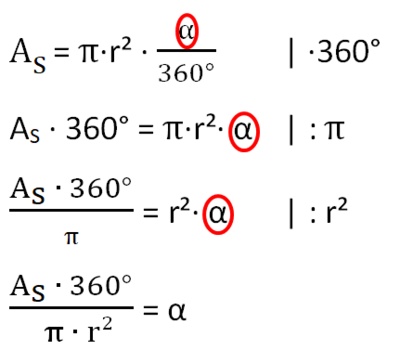Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (26 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
<br> | <br> | ||
{{Navigation|[[Benutzer:Buss-Haskert/Kreis und Zylinder|Kreis und Zylinder - Startseite]]<br> | {{Navigation|[[Benutzer:Buss-Haskert/Kreis und Zylinder|Kreis und Zylinder - Startseite]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang|1 Kreisumfang]]<br> | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang|1 Kreisumfang]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisfläche|2 Kreisfläche]]<br> | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisfläche|2 Kreisfläche]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile|3 Kreisteile]]<br> | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile|3 Kreisteile]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Zylinder|4 Zylinder]] | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Zylinder|4 Zylinder]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Zusammengesetzte Körper|5 Zusammengesetzte Körper]] | |||
}} | }} | ||
<br> | |||
==3 Kreisteile== | ==3 Kreisteile== | ||
| Zeile 14: | Zeile 16: | ||
<ggb_applet id="KTdCkyVv" width="950" height="550" border="888888" /> | <ggb_applet id="KTdCkyVv" width="950" height="550" border="888888" /> | ||
Applet von GeoGebra Translation Team German, Pöchtrager<br> | Applet von GeoGebra Translation Team German, Pöchtrager<br> | ||
{{Box|Übung 1 - Begriffe|Bearbeite die nachfolgenden Apps (Autor: FLINK-Team, GeoGebra)|Üben}} | |||
{{LearningApp|app=ph5k4j3kj21|width=100%|height=600px}} | |||
<ggb_applet id="vfesfj5z" width="800" height="640" border="888888" /> | |||
===3.1 Kreisring=== | ===3.1 Kreisring=== | ||
| Zeile 31: | Zeile 38: | ||
{{Lösung versteckt|1=Den Flächeninhalt des schwarzen, blauen und roten Ringes berechne ebenso. Wähle jeweils der Radius des äußeren und inneren Kreises passend:<br> | {{Lösung versteckt|1=Den Flächeninhalt des schwarzen, blauen und roten Ringes berechne ebenso. Wähle jeweils der Radius des äußeren und inneren Kreises passend:<br> | ||
schwarzer Ring: r<sub>a</sub> = 32cm; r<sub>i</sub> = 24cm.<br> | schwarzer Ring: r<sub>a</sub> = 32cm; r<sub>i</sub> = 24cm.<br> | ||
blauer Ring: | blauer Ring: r<sub>a</sub> = 24cm; r<sub>i</sub> = 16cm.<br> | ||
roter Ring: r<sub>a</sub> = | roter Ring: r<sub>a</sub> = 16cm; r<sub>i</sub> = 8cm.<br> | ||
Der gelbe Kreis ist ein ganzer Kreis mit dem Radius r = 8cm.|2=Tipp 3|3=Verbergen}} | Der gelbe Kreis ist ein ganzer Kreis mit dem Radius r = 8cm.|2=Tipp 3|3=Verbergen}} | ||
{{Lösung versteckt|1=Vergleiche deine Lösung zu a)<br> | {{Lösung versteckt|1=Vergleiche deine Lösung zu a)<br> | ||
| Zeile 49: | Zeile 56: | ||
A<sub>Kreisring</sub> = π·r<sub>a</sub>² - π·r<sub>i</sub>² | (π als gleichen Faktor ausklammern)<br> | A<sub>Kreisring</sub> = π·r<sub>a</sub>² - π·r<sub>i</sub>² | (π als gleichen Faktor ausklammern)<br> | ||
= π·(r²<sub>a</sub> - r²<sub>i</sub>)|3=Arbeitsmethode}}<br> | = π·(r²<sub>a</sub> - r²<sub>i</sub>)|3=Arbeitsmethode}}<br> | ||
Die Formel wird veranschaulicht im nachfolgenden Applet:<br> | Die Formel wird veranschaulicht im nachfolgenden Applet: https://www.geogebra.org/m/mdksvgq6<br> | ||
<ggb_applet id="mdksvgq6" width="1074" height="814" border="888888" /> | <ggb_applet id="mdksvgq6" width="1074" height="814" border="888888" /> | ||
| Zeile 56: | Zeile 63: | ||
{{Box|Übung | {{Box|Übung 2|Löse die Aufgabe aus dem Buch und prüfe deine Ergebnisse mit dem Applet oben. | ||
* S. 150 Nr. 6|Üben}} | * S. 150 Nr. 6|Üben}} | ||
{{Lösung versteckt|1=Berechne zunächst r<sub>2</sub>.<br> | {{Lösung versteckt|1=Berechne zunächst r<sub>2</sub>.<br> | ||
r<sub>2</sub>=r<sub>1</sub>+a|2=Tipp zu Nr. 6b|3=Verbergen}} | r<sub>2</sub>=r<sub>1</sub>+a|2=Tipp zu Nr. 6b|3=Verbergen}} | ||
{{Box| | {{Box|Übung 3|Löse auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/kreis/kreisflaeche.shtml '''Aufgabenfuchs'''] die Aufgaben | ||
* 5 | * 5 | ||
* 23|Üben}} | * 23 (Profi-Aufgabe, freiwillig)|Üben}} | ||
{{Box|Übung | {{Lösung versteckt|1=gegeben: A Kreisring und d, also auch der äußere Radius r<sub>a</sub>.<br> | ||
Stelle die Gleichung für den Flächeninhalt des Kreisringes nach <sub>i</sub> um:<br> | |||
A = π·<math>r_a^2</math> - π·<math>r_i^2</math> |+π·<math>r_i^2</math><br> | |||
π·<math>r_i^2</math> + A = π·<math>r_a^2</math> |-A<br> | |||
π·<math>r_i^2</math> = π·<math>r_a^2</math> - A |:π<br> | |||
<math>r_i^2</math> = <math>\tfrac{\pi \cdot r_a^2 - A}{\pi}</math> |<math>\surd</math><br> | |||
<math>r_i^2</math> = <math>\sqrt{\tfrac{\pi \cdot r_a^2 - A}{\pi}}</math> |Werte einsetzen<br> | |||
<math>r_i</math> = ...|2=Formel umstellen Nr. 23|3=Verbergen}} | |||
{{Box|Übung 4 - Anwendung|Löse die nachfolgenden LearningApps.|Üben}} | |||
{{LearningApp|app=ppwg6p33j21|width=100%|height=600px}} | {{LearningApp|app=ppwg6p33j21|width=100%|height=600px}} | ||
{{LearningApp|app=pnpgfj31a21|width=100%|heigth=600px}} | {{LearningApp|app=pnpgfj31a21|width=100%|heigth=600px}} | ||
| Zeile 79: | Zeile 95: | ||
<br> | <br> | ||
{{Box|Übung | {{Box|Übung 5|Löse die folgende LearningApp zu Mittelpunktswinkeln und ihren Bezeichnungen|Üben}} | ||
{{LearningApp|app=p3o29ay9n20|width=100%|heigth=600px}} | {{LearningApp|app=p3o29ay9n20|width=100%|heigth=600px}} | ||
{{Box|1=Kreisausschnitt und Kreisbogen|2=Übertrage den Hefteintrag und die Beispiele in dein Heft.<br>[[Datei:Hefteintrag Kreisteile.png|rahmenlos|800x800px]]|3=Arbeitsmethode}} | {{Box|1=Kreisausschnitt und Kreisbogen|2=Übertrage den Hefteintrag und die Beispiele in dein Heft.<br>[[Datei:Hefteintrag Kreisteile.png|rahmenlos|800x800px]]|3=Arbeitsmethode}} | ||
| Zeile 103: | Zeile 113: | ||
= 6,3 (cm)<br></div> | = 6,3 (cm)<br></div> | ||
</div> | </div> | ||
{{Box|Übung 6|Löse auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/kreis/teilkreis.shtml '''Aufgabenfuchs'''] die Aufgaben | |||
* 1 | |||
* 2 | |||
* 3 | |||
* 4 | |||
* 5|Üben}} | |||
<br> | <br> | ||
<div class="grid"> | <div class="grid"> | ||
| Zeile 110: | Zeile 129: | ||
<br> | <br> | ||
{{Box|Übung | {{Box|Übung 7|Löse die Aufgaben aus dem Buch. Achte auf eine ausführliche und übersichtliche Darstellung. | ||
* S. 138 Nr. 2 | * S. 138 Nr. 2 | ||
* S. 138 Nr. 3|Üben}} | * S. 138 Nr. 3|Üben}} | ||
| Zeile 116: | Zeile 135: | ||
<ggb_applet id="hgc5mhz3" width="936" height="814" border="888888" /> | <ggb_applet id="hgc5mhz3" width="936" height="814" border="888888" /> | ||
<br> | <br> | ||
{{Box|1=Formeln umstellen|2=[[Datei:Aufgabe Formel Kreisausschnitt umstellen.png|rechts|rahmenlos| | |||
===Formeln umstellen=== | |||
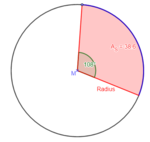
{{Box|1=Formeln umstellen|2=[[Datei:Aufgabe Formel Kreisausschnitt umstellen.png|rechts|rahmenlos|150x150px]] a) geg: A<sub>S</sub> = 38,6 cm²; α = 108°<br> | |||
ges: r<br> | ges: r<br> | ||
<br> | <br> | ||
<br> | <br> | ||
[[Datei:Aufgabe Formel Kreisbogen umstellen.png|rechts|rahmenlos| | <br> | ||
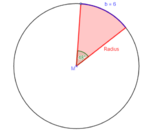
[[Datei:Aufgabe Formel Kreisbogen umstellen.png|rechts|rahmenlos|150x150px]] b) geg: b = 6cm; α = 48°<br> | |||
ges: r <br> | ges: r <br> | ||
<br> | <br> | ||
<br> | <br> | ||
[[Datei:Formel umstellen Kreisausschnitt nach Winkel.png|rechts| | <br> | ||
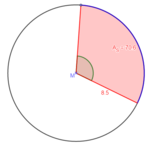
[[Datei:Formel umstellen Kreisausschnitt nach Winkel.png|rechts|rahmenlos|150x150px]] c) geg: r = 8,5 cm; A<sub>S</sub> = 70,6 cm²<br> | |||
ges: α<br> | ges: α<br> | ||
<br> | |||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 133: | Zeile 159: | ||
{{Lösung versteckt|1=[[Datei:Formel Kreisausschnitt umstellen nach Winkel.png|rahmenlos|400x400px]]|2=Tipp zu c|3=Verbergen}} | {{Lösung versteckt|1=[[Datei:Formel Kreisausschnitt umstellen nach Winkel.png|rahmenlos|400x400px]]|2=Tipp zu c|3=Verbergen}} | ||
{{#ev:youtube|gct3CCDPsH0|800|center|||start=120&end=176}} | {{#ev:youtube|gct3CCDPsH0|800|center|||start=120&end=176}} | ||
{{Box|Übung | {{Box|Übung 8|Löse die Aufgaben aus dem Buch. Stelle dazu die entsprechenden Formeln nach der gesuchten Größe um. Prüfe deine Lösung mit dem Applet oben. | ||
* S. 138 Nr. 4 | * S. 138 Nr. 4 b,c | ||
* S. 138 Nr. 5 | * S. 138 Nr. 5 a,c | ||
* S. 138 Nr. 6 | * S. 138 Nr. 6 | ||
* S. 138 Nr. 7 (Wähle hier die Übungen aus, bei denen du noch Schwierigkeiten in Nr. 4 bzw. Nr. 5 hattest.)|Üben}} | * S. 138 Nr. 7 (Wähle hier die Übungen aus, bei denen du noch Schwierigkeiten in Nr. 4 bzw. Nr. 5 hattest.)|Üben}} | ||
{{Lösung versteckt|1=geg: b und r<br> | |||
ges: α<br> | |||
Stelle die Kreisbogen-Formel nach α um:<br> | |||
b = 2πr·<math>\tfrac{\alpha}{360}</math> |·360 ("Nenner weg")<br> | |||
360°·b = 2πr·α | : (2πr)<br> | |||
<math>\tfrac{360 \cdot b}{2\pi r}</math> = α | Werte einsetzen<br> | |||
... |2=Tipp zu Nr. 5a (Formel umstellen)|3=Verbergen}} | |||
{{Lösung versteckt|1=Lösungen:<br> | |||
4b) r ≈ 1,11 cm; 4c) r ≈ 20,0 cm<br> | |||
5a) α ≈ 80,21°; 5c) α ≈ 144,3°|2=Vergleiche deine Lösungen zu Nr. 4 und 5|3=Verbergen}} | |||
{{Lösung versteckt|1=Der Bogen b ist genauso lang wie der Radius r...<br> | |||
1. Idee (leicht): Setzte eine Zahl ein, z.B. b=1, dann ist auch r=1 (b soll genauso lang sein wie r) und stelle die Gleichung nach α um:<br> | |||
b=2·π·r·<math>\tfrac{\alpha}{360}</math><br> | |||
1=2·π·1·<math>\tfrac{\alpha}{360}</math> |·360<br> | |||
360 = 2·π·1·α |:(2·π)<br> | |||
<math>\tfrac{360}{2\pi}</math> = α<br> | |||
57,3° ≈ α<br> | |||
<br> | |||
2. Idee (schwieriger, allgemein): Schreibe die Gleichung mit nur einer Variablen, z.B. r, denn b=r.<br> | |||
b=2·π·r·<math>\tfrac{\alpha}{360}</math> &nbps; |b=r<br> | |||
r=2·π·r·<math>\tfrac{\alpha}{360}</math> |·360<br> | |||
r·360 = 2·π·r·α |:(2·π·r)<br> | |||
<math>\tfrac{360}{2\pi r}</math> = α |r kürzen <br> | |||
<math>\tfrac{360}{2\pi}</math> = α<br> | |||
57,3° ≈ α<br> | |||
<br> | |||
b) Gehe ebenso vor, also z.B. b=2, r=1 (b ist doppelt so groß wie r)<br> | |||
oder b = 2r einsetzen<br> | |||
Lösung: α ≈ 114,6°<br> | |||
Gege ebenso vor, also z.B. b=1, r=2 (b ist halb so groß wie r)<br> | |||
oder b=0,5r<br> | |||
α ≈ 28,6°<br>|2=Tipp zu Nr. 6|3=Verbergen}} | |||
===Anwendungsaufgaben=== | ===Anwendungsaufgaben=== | ||
{{Box|Übung | {{Box|Übung 9 - Anwendungen|Löse die Aufgabe aus dem Buch und die Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/flaeche/kreis/kreis.shtml '''Aufgabenfuchs'''] | ||
* S. 138 Nr. 8 | * S. 138 Nr. 8 | ||
* 12 | * 12 | ||
| Zeile 150: | Zeile 209: | ||
* 42 | * 42 | ||
* 43|Üben}} | * 43|Üben}} | ||
{{Lösung versteckt|1=Du findest im Aufgabentext Informationen zum Radius und zum Mittelpunktswinkel. |2=Tipp zu Nr. 8|3=Verbergen}} | |||
{{Box|Übung | {{Box|Übung 10 - Profiaufgaben|[[Datei:Scheibenwischeraufgabe.png|rechts|rahmenlos|300x300px]]* Scheibenwischer<br> | ||
Der Scheibenwischer eines Autos hat eine Länge von 48cm. Vom Drehpunkt bis zum unteren Ende des Wischerblattes sind es 16cm. Der Scheibenwischer | Der Scheibenwischer eines Autos hat eine Länge von 48cm. Vom Drehpunkt bis zum unteren Ende des Wischerblattes sind es 16cm. Der Scheibenwischer schwenkt über einen Winkel von 150° hin und her. Berechne den Flächeninhalt der erfassten Fläche. | ||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 158: | Zeile 218: | ||
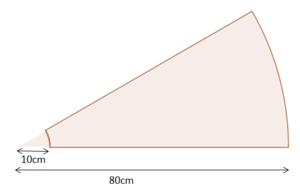
[[Datei:Wendeltreppe Stufe.png|rechts|rahmenlos|300x300px]]* Wendeltreppe<br> | [[Datei:Wendeltreppe Stufe.png|rechts|rahmenlos|300x300px]]* Wendeltreppe<br> | ||
Eine Wendeltreppe besteht aus 12 Stufen, die zusammen eine vollständige Drehung ergeben. Die Stufen einer Wendeltreppe haben die im Bild angegebenen Maße. Bestimme den Flächeninhalt einer Treppenstufe.|Üben}} | Eine Wendeltreppe besteht aus 12 Stufen, die zusammen eine vollständige Drehung ergeben. Die Stufen einer Wendeltreppe haben die im Bild angegebenen Maße. Bestimme den Flächeninhalt einer Treppenstufe.|Üben}} | ||
{{Lösung versteckt|1=Verwende zur Überprüfung deiner Rechnungen das Applet:<br> | {{Lösung versteckt|1=Verwende zur Überprüfung deiner Rechnungen das Applet:<br>Originallink: https://www.geogebra.org/m/ruaau9qb<br> | ||
<ggb_applet id="ruaau9qb" width="1904" height="948" border="888888" /><br>|2=Tipp Animation|3=Verbergen}} | <ggb_applet id="ruaau9qb" width="1904" height="948" border="888888" /><br>|2=Tipp Animation|3=Verbergen}} | ||
{{Lösung versteckt|1=Es handelt sich um einen Ausschnitt eines Kreisringes.<br> | {{Lösung versteckt|1=Es handelt sich um einen Ausschnitt eines Kreisringes.<br> | ||
Aktuelle Version vom 19. April 2024, 14:28 Uhr
1 Kreisumfang
2 Kreisfläche
3 Kreisteile
4 Zylinder
5 Zusammengesetzte Körper
3 Kreisteile
Welche Arten von Kreisteilen gibt es?
Mache dich mit den verschiedenen Begriffen vertraut:

Applet von GeoGebra Translation Team German, Pöchtrager

3.1 Kreisring
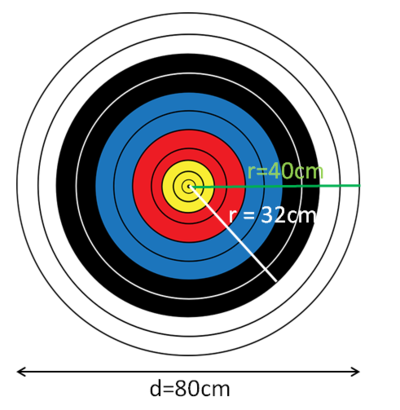
Für die Fläche des weißen Ringes, berechne zunächst den Flächeninhalt der gesamte Scheibe A1 mit dem Radius raußen = 40cm. Subtrahiere anschließend den Flächeninhalt des inneren Kreises A2 mit dem Radius rinnen = 32cm.
AKreisring weiß = A1 - A2
= π·ra² - π·ri²
= π·40² - π·32²
= π·(40² - 32²)
Den Flächeninhalt des schwarzen, blauen und roten Ringes berechne ebenso. Wähle jeweils der Radius des äußeren und inneren Kreises passend:
schwarzer Ring: ra = 32cm; ri = 24cm.
blauer Ring: ra = 24cm; ri = 16cm.
roter Ring: ra = 16cm; ri = 8cm.
Vergleiche deine Lösung zu a)
Aweiß = 1809,56 cm²
Aschwarz = 1407,43 cm²
Ablau = 1005,31 cm²
Arot = 603,19 cm²
Agelb = 201,06 cm²
Für die Berechnungen der Flächeninhalte der Kreisringe hast du immer vom äußeren Kreis den inneren Kreis subtrahiert. Leite so die Formel her:
AKreisring = Aaußen - Ainnen
= π·r²a - π·r²i | π als gleichen Faktor ausklammern
Die Formel wird veranschaulicht im nachfolgenden Applet: https://www.geogebra.org/m/mdksvgq6

Berechne zunächst r2.
gegeben: A Kreisring und d, also auch der äußere Radius ra.
Stelle die Gleichung für den Flächeninhalt des Kreisringes nach i um:
A = π· - π· |+π·
π· + A = π· |-A
π· = π· - A |:π
= |
= |Werte einsetzen
3.2 Kreisausschnitt AS und Kreisbogen b
Beobachte den Zusammenhang zwischen der Fläche des Kreisausschnittes und dem Mittelpunktswinkel α im nachfolgenden Applet:

Applet von IT Wombat
Beispiele:
geg: r = 5cm; α = 72°
Berechne den Flächeninhalt des Kreisausschnittes AS:
AS = π·r²· |Werte einsetzen
= π·5²·
b = 2·π·r· |Werte einsetzen
= 2·π·5·
Prüfe deine Lösungen mithilfe des Applets:

Formeln umstellen
geg: b und r
ges: α
Stelle die Kreisbogen-Formel nach α um:
b = 2πr· |·360 ("Nenner weg")
360°·b = 2πr·α | : (2πr)
= α | Werte einsetzen
Lösungen:
4b) r ≈ 1,11 cm; 4c) r ≈ 20,0 cm
Der Bogen b ist genauso lang wie der Radius r...
1. Idee (leicht): Setzte eine Zahl ein, z.B. b=1, dann ist auch r=1 (b soll genauso lang sein wie r) und stelle die Gleichung nach α um:
b=2·π·r·
1=2·π·1· |·360
360 = 2·π·1·α |:(2·π)
= α
57,3° ≈ α
2. Idee (schwieriger, allgemein): Schreibe die Gleichung mit nur einer Variablen, z.B. r, denn b=r.
b=2·π·r· &nbps; |b=r
r=2·π·r· |·360
r·360 = 2·π·r·α |:(2·π·r)
= α |r kürzen
= α
57,3° ≈ α
b) Gehe ebenso vor, also z.B. b=2, r=1 (b ist doppelt so groß wie r)
oder b = 2r einsetzen
Lösung: α ≈ 114,6°
Gege ebenso vor, also z.B. b=1, r=2 (b ist halb so groß wie r)
oder b=0,5r
Anwendungsaufgaben
Verwende zur Überprüfung deiner Rechnungen das Applet:
Originallink: https://www.geogebra.org/m/ruaau9qb

Es handelt sich um einen Ausschnitt eines Kreisringes.