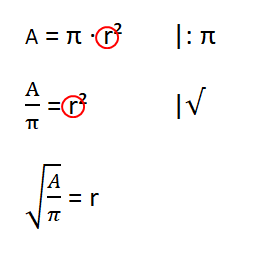Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisfläche: Unterschied zwischen den Versionen
K (LearningApp ergänzt) Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (39 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
<br> | <br> | ||
{{Navigation|[[Benutzer:Buss-Haskert/Kreis und Zylinder|Kreis und Zylinder - Startseite]]<br> | {{Navigation|[[Benutzer:Buss-Haskert/Kreis und Zylinder|Kreis und Zylinder - Startseite]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang|1 Kreisumfang]]<br> | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang|1 Kreisumfang]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisfläche|2 Kreisfläche]]<br> | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisfläche|2 Kreisfläche]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile|3 Kreisteile]] | [[Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile|3 Kreisteile]]<br> | ||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Zylinder|4 Zylinder]]<br> | |||
[[Benutzer:Buss-Haskert/Kreis und Zylinder/Zusammengesetzte Körper|5 Zusammengesetzte Körper]] | |||
}} | }} | ||
<br> | <br> | ||
| Zeile 34: | Zeile 36: | ||
b) Welche Figur entsteht?<br> | b) Welche Figur entsteht?<br> | ||
c) Leite damit eine Formel für die Kreisfläche her.|Unterrichtsidee}} | c) Leite damit eine Formel für die Kreisfläche her.|Unterrichtsidee}} | ||
Originallink https://www.geogebra.org/m/KvkYnd6A<br> | |||
Applet von Anthony Or. Education Bureau<br> | <ggb_applet id="RvbbbEAg" width="980" height="566" border="888888" /> | ||
<small>Applet von Anthony Or. Education Bureau</small><br> | |||
{{Lösung versteckt|1=Das Applet ist einfacher dargestellt und gibt bei er neu entstandenen Figur die Längen an. Kannst du nun eine Formel für den Flächeninhalt herleiten?<br> | {{Lösung versteckt|1=Das Applet ist einfacher dargestellt und gibt bei er neu entstandenen Figur die Längen an. Kannst du nun eine Formel für den Flächeninhalt herleiten?<br> | ||
Originallink https://www.geogebra.org/m/cQeSV4tC | |||
<ggb_applet id="jpx7xqUb" width="651" height="300" border="888888" /> | <ggb_applet id="jpx7xqUb" width="651" height="300" border="888888" /> | ||
Applet von R. Schmidt|2=Tipp 1|3=Verbergen}} | Applet von R. Schmidt|2=Tipp 1|3=Verbergen}} | ||
| Zeile 60: | Zeile 64: | ||
Eine weitere Möglichkeit, den Flächeninhalt eines Kreises abzuschätzen, zeigt das folgende Applet von Pöchtrager:<br> | Eine weitere Möglichkeit, den Flächeninhalt eines Kreises abzuschätzen, zeigt das folgende Applet von Pöchtrager:<br> | ||
Beschreibe!<br> | Beschreibe!<br> | ||
Originallink https://www.geogebra.org/m/cQeSV4tC | |||
<ggb_applet id="cQeSV4tC" width="800" height="500" border="888888" /> | <ggb_applet id="cQeSV4tC" width="800" height="500" border="888888" /> | ||
<br> | <br> | ||
<br> | <br> | ||
{{Box|1=Kreisfläche - Formel|2=Den Flächeninhalt A eines Kreises kann man mithilfe des Radius r berechnen:<br><br> | {{Box|1=Kreisfläche - Formel|2=[[Datei:Bezeichnungen am Kreis.png|rechts|rahmenlos]]Den <span style="color:red">'''Flächeninhalt A''' </span>eines Kreises kann man mithilfe des Radius r berechnen:<br><br> | ||
<big><big>''' A = π r²'''</big></big><br> | <big><big>''' A = π r²'''</big></big><br> | ||
<br> | <br> | ||
| Zeile 102: | Zeile 107: | ||
ges: r<br> | ges: r<br> | ||
A = π · r² |: π<br> | A = π · r² |: π<br> | ||
<math>\tfrac{A}{\pi}</math> = | <math>\tfrac{A}{\pi}</math> = r<sup>2</sup> |<math>\surd</math><br> | ||
<math>\sqrt{\tfrac{A}{\pi}}</math> = r |Wert einsetzen<br> | <math>\sqrt{\tfrac{A}{\pi}}</math> = r |Wert einsetzen<br> | ||
<math>\sqrt{\tfrac{7,0}{\pi}}</math> = r<br> | <math>\sqrt{\tfrac{7,0}{\pi}}</math> = r<br> | ||
| Zeile 112: | Zeile 117: | ||
d = 2·r; Berechne zunächst r:<br> | d = 2·r; Berechne zunächst r:<br> | ||
A = π · r² |: π<br> | A = π · r² |: π<br> | ||
<math>\tfrac{A}{\pi}</math> = | <math>\tfrac{A}{\pi}</math> = r<sup>2</sup> |<math>\surd</math><br> | ||
<math>\sqrt{\tfrac{A}{\pi}}</math> = r |Wert einsetzen<br> | <math>\sqrt{\tfrac{A}{\pi}}</math> = r |Wert einsetzen<br> | ||
<math>\sqrt{\tfrac{18,10}{\pi}}</math> = r<br> | <math>\sqrt{\tfrac{18,10}{\pi}}</math> = r<br> | ||
| Zeile 132: | Zeile 137: | ||
{{Box|Übung 2|Löse die Aufgaben aus dem Buch. Schreibe ausführlich und übersichtlich. Notiere - falls nötig - und die Umstellung der Formel. Vergleiche deine Lösungen und hake ab. | {{Box|Übung 2|Löse die Aufgaben aus dem Buch. Schreibe ausführlich und übersichtlich. Notiere - falls nötig - und die Umstellung der Formel. Vergleiche deine Lösungen und hake ab. | ||
* S. 131 Nr. 1 (Wähle eine | * S. 131 Nr. 1 (Wähle eine Aufgabe aus.) | ||
* S. 131 Nr. 2 (Wähle eine Aufgabe aus.) | * S. 131 Nr. 2 (Wähle eine Aufgabe aus.) | ||
* S. 132 Nr. 3 (Wähle aus: a und c oder b und d) | * S. 132 Nr. 3 (Wähle aus: a und c oder b und d) | ||
* S. 132 Nr. 4 |Üben}} | * S. 132 Nr. 4 |Üben}} | ||
Prüfe deine Lösungen mithilfe der LearningApp. Trage deine Lösung ein und klicke den Prüfbutton. Hake im Heft deine Ergebnisse ab.<br> | {{Lösung versteckt|1=Prüfe deine Lösungen mithilfe der LearningApp. Trage deine Lösung ein und klicke den Prüfbutton. Hake im Heft deine Ergebnisse ab.<br> | ||
{{LearningApp|app=puttncjp521|width=100%|height=600px}} | {{LearningApp|app=puttncjp521|width=100%|height=600px}} | ||
{{LearningApp|app=pc4e9ni8k21|width=100%|height=400px}} | {{LearningApp|app=pc4e9ni8k21|width=100%|height=400px}}|2=Prüfe deine Lösungen|3=Verbergen}} | ||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 176: | Zeile 181: | ||
====Geometrische Anwendungen==== | ====Geometrische Anwendungen==== | ||
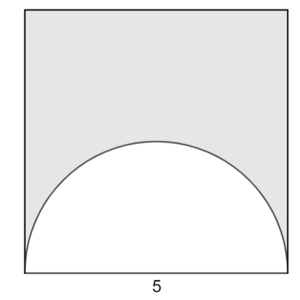
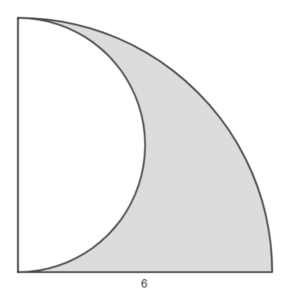
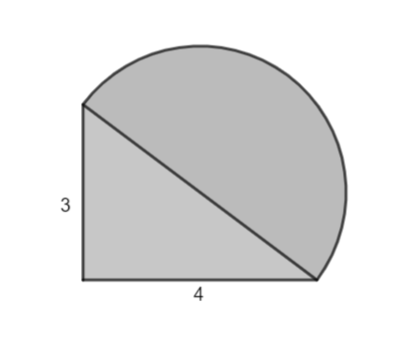
{{Box|1=Geometrische Anwendungen - Beispiele|2=Berechne den Flächeninhalt der Figuren. Notiere deine Überlegungen übersichtlich. | |||
<div class="grid"> | |||
<div class="width-1-3">1. Beispiel:<br> | |||
[[Datei:Halbkreis im Quadrat 2.png|rahmenlos]]<br> | |||
A = A<sub>Quadrat</sub> - A<sub>Halbkreis</sub><br> | |||
= a² - <math>\tfrac{1}{2}</math>·π·r²<br> | |||
= 5² - <math>\tfrac{1}{2}</math>·π·2,5²<br> | |||
≈ 25 - 9,82<br> | |||
= 15,18 [cm²] <br> | |||
</div> | |||
<div class="width-1-3">2. Beispiel:<br> | |||
[[Datei:Halbkreis im Viertelkreis.png|rahmenlos|300x300px]]<br> | |||
A = A<sub>Viertelkreis</sub> - A<sub>Halbkreis</sub><br> | |||
= <math>\tfrac{1}{4}</math>·π·<math>r_1^2</math> - <math>\tfrac{1}{2}</math>·π·<math>r_2^2</math><br> | |||
= <math>\tfrac{1}{4}</math>·π·6² - <math>\tfrac{1}{2}</math>·π·3²<br> | |||
≈ 28,27 - 14,14<br> | |||
= 14,13 [cm²] <br> | |||
</div> | |||
<div class="width-1-3">3. Beispiel:<br> | |||
[[Datei:Rechtwinkliges Dreieck mit Halbkreis.png|rahmenlos|400x400px]]<br> | |||
Berechne den Radius des Halbkreises (mit dem Satz des Pythagoras):<br> | |||
d² = 3² + 4²<br> | |||
d = <math>\sqrt{3^2 + 4^2}</math><br> | |||
d = 5 [cm]; also r = 5:2 = 2,5 [cm]<br> | |||
A = A<sub>Dreieck</sub> + A<sub>Halbkreis</sub><br> | |||
= <math>\tfrac{1}{2}</math>·g·h + <math>\tfrac{1}{2}</math>·π·<math>r^2</math><br> | |||
= <math>\tfrac{1}{2}</math>·3·4 - <math>\tfrac{1}{2}</math>·π·2,5²<br> | |||
≈ 6 + 9,82<br> | |||
= 15,82 [cm²] <br> | |||
</div> | |||
</div>|3=Arbeitsmethode}} | |||
{{Box|Übung 4 - Geometrische Anwendungen|Löse die Aufgaben aus dem Buch. Notiere deine Überlegungen ausführlich und übersichtlich. Zeichne - falls nötig - Teilskizzen. Prüfe deine Lösungen und hake ab. | {{Box|Übung 4 - Geometrische Anwendungen|Löse die Aufgaben aus dem Buch. Notiere deine Überlegungen ausführlich und übersichtlich. Zeichne - falls nötig - Teilskizzen. Prüfe deine Lösungen und hake ab. | ||
* S. 132 Nr. 6 | * S. 132 Nr. 6 | ||
| Zeile 222: | Zeile 260: | ||
{{Lösung versteckt|1=Umfang u: Das Dreieck ist ein gleichschenklig rechtwinkliges Dreieck. Die Basis ist 4cm lang. Bestimme die Länge der Schenkel mit dem Satz des Pythagoras.<br> | {{Lösung versteckt|1=Umfang u: Das Dreieck ist ein gleichschenklig rechtwinkliges Dreieck. Die Basis ist 4cm lang. Bestimme die Länge der Schenkel mit dem Satz des Pythagoras.<br> | ||
[[Datei:S. 132 Nr. 6c Tipp.png|rahmenlos]]<br> | [[Datei:S. 132 Nr. 6c Tipp.png|rahmenlos]]<br> | ||
x<sup>2</sup> + x<sup>2</sup> = 4<sup>2</sup> &124;<br> | |||
2x<sup>2</sup> = 16 <br> | |||
… <br> | |||
Lösung: u = 11,9cm<br> | Lösung: u = 11,9cm<br> | ||
Flächeninhalt A: Die Fläche setzt sich zusammen aus dem Flächeninhalt A<sub>1</sub> des Dreiecks und dem Flächeninhalt A<sub>2</sub> des Halbkreises.<br> | Flächeninhalt A: Die Fläche setzt sich zusammen aus dem Flächeninhalt A<sub>1</sub> des Dreiecks und dem Flächeninhalt A<sub>2</sub> des Halbkreises.<br> | ||
| Zeile 270: | Zeile 311: | ||
====Sachsituationen==== | ====Sachsituationen==== | ||
{{LearningApp|app=py733oge321|width=100%|height=500px}} | {{LearningApp|app=py733oge321|width=100%|height=500px}} | ||
{{Box|1=Einstiegsaufgabe - Kreisfläche|2=Betrachte das nachfolgende Applet und beantworte die folgenden Fragen:<br> | |||
[[Datei:Quadrat mit Kreis.png|rahmenlos]][[Datei:Quadrat mit 4 Kreisen.png|rahmenlos]] | |||
*Aus einem Quadrat der Seitenlänge a wird ein maximaler Kreis ausgeschnitten. Wieviel Prozent beträgt der Abfall? | |||
*Jetzt werden 4, 9, 16 gleich große Kreise ausgeschnitten. Wieviel Prozent beträgt nun der Abfall? | |||
*Auch wenn das Ergebnis zunächst überraschen mag, kann man es einfach erklären. Betrachte für n > 1 den Zusammenhang zwischen dem hervorgehobenen kleinen Quadrat mit kleinem Kreis und der Figur für n = 1. Wie entstehen diese Figuren auseinander? Was bedeutet das für die Flächen?|3=Meinung}} | |||
Originallink: https://www.geogebra.org/m/krnwuf2s | |||
<ggb_applet id="awkjt4py" width="1500" height="850" border="888888" /> | |||
<small>Applet von Hans-Jürgen Elschenbroich</small> | |||
{{Box|Übung 6 - Sachsituationen|Löse so viele Aufgaben, dass du mindestes 7 Sternchen sammelst. Notier deine Rechnungen ausführlich und übersichtlich. Prüfe deine Lösungen und hake ab. | {{Box|Übung 6 - Sachsituationen|Löse so viele Aufgaben, dass du mindestes 7 Sternchen sammelst. Notier deine Rechnungen ausführlich und übersichtlich. Prüfe deine Lösungen und hake ab. | ||
* S. 133 Nr. 10 (*) | * S. 133, Nr. 10 (*) | ||
* S. 134 Nr. 16 (*) | * S. 134, Nr. 16 (*) | ||
* S. 134 Nr. 17 (*) | * S. 134, Nr. 17 (*) | ||
* S. 134 Nr. 18 (*) | * S. 134, Nr. 18 (*) | ||
* S. 134 Nr. 20 (**) | * S. 134, Nr. 19 (*) | ||
* S. 134 Nr. 21 (**) | * S. 134, Nr. 20 (**) | ||
* S. 150 Nr. 7 (*) | * S. 134, Nr. 21 (**) | ||
* S. 150 Nr. 8 (**) | * S. 150, Nr. 7 (*) | ||
* S. 150 Nr. 9 (**)|Üben}} | * S. 150, Nr. 8 (**) | ||
* S. 150, Nr. 9 (**)|Üben}} | |||
{{Lösung versteckt|1=Der Flächeninhalt des Verschnittes berechnest du, indem du die Kreisflächen von der Quadratfläche subtrahierst. Bestimme für die Berechnung der Kreisflächen jeweils den Radius der Kreise.<br> | {{Lösung versteckt|1=Der Flächeninhalt des Verschnittes berechnest du, indem du die Kreisflächen von der Quadratfläche subtrahierst. Bestimme für die Berechnung der Kreisflächen jeweils den Radius der Kreise.<br> | ||
A<sub>Verschnitt</sub> = A<sub>Quadrat</sub> - A<sub>Kreise</sub><br> | A<sub>Verschnitt</sub> = A<sub>Quadrat</sub> - A<sub>Kreise</sub><br> | ||
= 80 · 80 - 1·π·40²<br> | = 80 · 80 - 1·π·40²<br> | ||
= | = 6400 - 5026,55<br> | ||
= 1373,45cm²<br> | = 1373,45cm²<br> | ||
Rechne weiter für die übrigen Figuren. Was fällt dir auf?<br> | Rechne weiter für die übrigen Figuren. Was fällt dir auf?<br> | ||
| Zeile 291: | Zeile 342: | ||
Die Flügellänge entspricht dem Radius, die Winderntefläche der Kreisfläche.<br> | Die Flügellänge entspricht dem Radius, die Winderntefläche der Kreisfläche.<br> | ||
Lösung: a) A ≈ 1122,21 m²<br> | Lösung: a) A ≈ 1122,21 m²<br> | ||
b) A ≈ 3848,45 m²|2=Tipp zu Nr. | b) A ≈ 3848,45 m²|2=Tipp zu Nr. 17|3=Verbergen}} | ||
{{Lösung versteckt|1=Die Kreisform entsteht, da die Bewässerungsanlagen sich kreisförmig drehen.<br> | {{Lösung versteckt|1=Die Kreisform entsteht, da die Bewässerungsanlagen sich kreisförmig drehen.<br> | ||
Um die ungenutzte Fläche zu berechnen, subtrahiere die Kreisfläche von der quadratischen Fläche.<br> | Um die ungenutzte Fläche zu berechnen, subtrahiere die Kreisfläche von der quadratischen Fläche.<br> | ||
| Zeile 309: | Zeile 360: | ||
Berechne den Flächeninhalt der kleinen und der große Pizza. Überlege dann '''auf''' wie viel Prozent der kleinen Pizza sich die Fläche der zweiten Pizza vergrößert hat.<br> Gegeben sind hier also G und G<sup>+</sup>.<br> | Berechne den Flächeninhalt der kleinen und der große Pizza. Überlege dann '''auf''' wie viel Prozent der kleinen Pizza sich die Fläche der zweiten Pizza vergrößert hat.<br> Gegeben sind hier also G und G<sup>+</sup>.<br> | ||
Berechne damit p<sup>+</sup>%. <br> | Berechne damit p<sup>+</sup>%. <br> | ||
Lösung: p<sup>+</sup>% = 191,7%, also ist p% = | Lösung: p<sup>+</sup>% = 191,7%, also ist p% = 91,7%|2=Tipp 3 zu Nr. 8 (alternative Lösung)|3=Verbergen}} | ||
{{Lösung versteckt|1=Die Umlaufbahn ist gesucht, also der Umfang u.<br> | {{Lösung versteckt|1=Die Umlaufbahn ist gesucht, also der Umfang u.<br> | ||
Tipp zur Bahngeschwindigkeit: Die Geschwindigkeit gibt an, welche Strecke in welcher Zeit zurückgelegt wird (in <math>\tfrac{km}{h}</math>. Du benötigst also die Strecke, die zurückgelegt wird und die Zeit, in der diese Strecke zurückgelegt wird.|2=Tipp 1 zu Nr. 9|3=Verbergen}} | |||
{{Lösung versteckt|1=Strecke: Länge der Umlaufbahn, also u.<br> | {{Lösung versteckt|1=Strecke: Länge der Umlaufbahn, also u.<br> | ||
Zeit: Der Satellit ist geostationär, er bewegt sich also genauso schnell, wie die Erde sich dreht. Für eine ganze Umlaufbahn benötigt er also 24 Stunden (einen Tag), denn die Erde dreht sich in 24 Stunde einmal um ihre Achse.<br> | Zeit: Der Satellit ist geostationär, er bewegt sich also genauso schnell, wie die Erde sich dreht. Für eine ganze Umlaufbahn benötigt er also 24 Stunden (einen Tag), denn die Erde dreht sich in 24 Stunde einmal um ihre Achse.<br> | ||
| Zeile 329: | Zeile 380: | ||
===Vermischte Übungen=== | ===Vermischte Übungen=== | ||
{{Box|Übung | {{Box|Übung 8|Bearbeite die nachfolgenden LearningApps.|Üben}} | ||
{{LearningApp|app=pf347f4x321|width=100%|height=600px}} | {{LearningApp|app=pf347f4x321|width=100%|height=600px}} | ||
{{Fortsetzung|weiter=3 Kreisteile|weiterlink=Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile}} | {{Fortsetzung|weiter=3 Kreisteile|weiterlink=Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile}} | ||
Aktuelle Version vom 15. April 2024, 06:35 Uhr
1 Kreisumfang
2 Kreisfläche
3 Kreisteile
4 Zylinder
5 Zusammengesetzte Körper
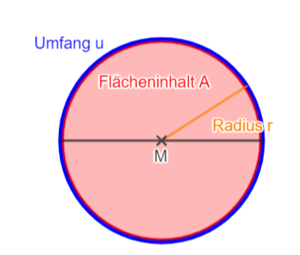
Kreisfläche A
Aufgabe aus dem Unterricht:
kleine Pizza: d1 = 17cm; Preis: 2 Stück kosten 2,49€
mittlere Pizza: d2 = 25cm; Preis: 2,49€
Du hast jeweils den Durchmesser der Pizzen gegeben, damit kannst du den Radius berechnen.
Um die Frage zu beantworten, musst du den Flächeninhalt der Pizzen berechnen können.
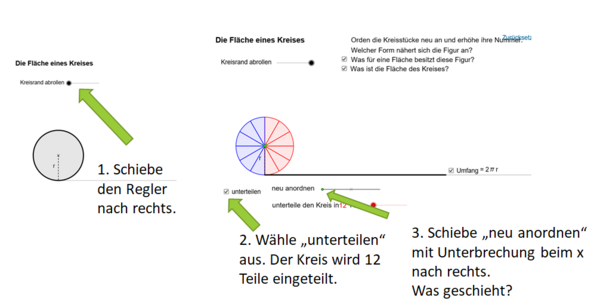
2.1 Kreisfläche - Herleitung der Formel
Originallink https://www.geogebra.org/m/KvkYnd6A

Applet von Anthony Or. Education Bureau
Das Applet ist einfacher dargestellt und gibt bei er neu entstandenen Figur die Längen an. Kannst du nun eine Formel für den Flächeninhalt herleiten?
Originallink https://www.geogebra.org/m/cQeSV4tC

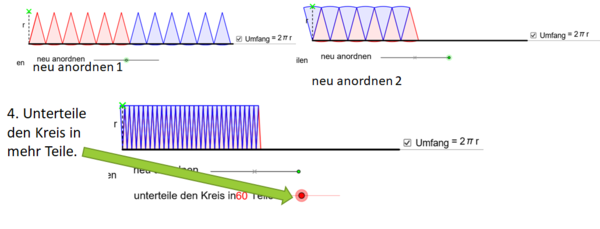
Die Fläche, die durch das Einteilen des Kreises und das Umlegen entsteht, hat annähernd die Form eines Rechtecks mit den Seitenlängen a= (halber Umfang) und b = r (Radius)
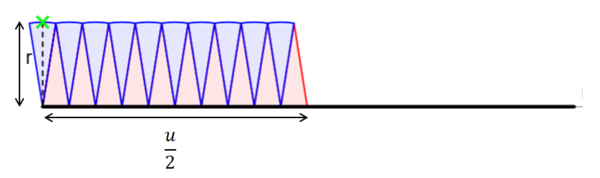

A = a·b | Setze für a den halben Umfang und für b den Radius ein.
= · r | Setze für u die Formel für den Umfang ein: u =2πr.
= · r | Kürze mit 2.
= πr · r | Fasse r·r zusammen.
Das Video fasst die Herleitung der Formel zusammen:
Eine weitere Möglichkeit, den Flächeninhalt eines Kreises abzuschätzen, zeigt das folgende Applet von Pöchtrager:
Beschreibe!
Originallink https://www.geogebra.org/m/cQeSV4tC

Merke dir die Formel mit dem Lied von Dorfuchs:
2.2 Kreisfläche - Berechnungen
Beispiele:
geg: r = 3,0 cm
ges: A
A = π · r² |Wert einsetzen
= π · 3,0²
geg: d = 5,0 cm
ges: A
r = = = 2,5 (cm)
A = π · r² |Wert einsetzen
= π · 2,5²
geg: A = 7,0 cm²
ges: r
A = π · r² |: π
= r2 |
= r |Wert einsetzen
= r
1,5 (cm) ≈ r
geg: A = 18,10 cm²
ges: d
d = 2·r; Berechne zunächst r:
A = π · r² |: π
= r2 |
= r |Wert einsetzen
= r
2,4 (cm) ≈ r
Prüfe deine Lösungen mithilfe der LearningApp. Trage deine Lösung ein und klicke den Prüfbutton. Hake im Heft deine Ergebnisse ab.
Radius r und Umfang u:
Wenn man den Radius r eines Kreises verdoppelt, verdreifacht, vervierfacht,... dannverdoppelt, verdreifacht, vervierfacht sich der Umfang u.
Radius r und Flächeninhalt A:
Wenn man den Radius r eines Kreises verdoppelt, verdreifacht, vervierfacht,... dannvervierfacht, verneunfacht, versechzehnfacht sich der Flächeninhalt A.
Prüfe deine Vermutung mit dem nachfolgenden GeoGebra-Applet:

2.3 Kreisfläche - Anwendungen
Jetzt kannst du die Einführungsaufgabe lösen: Bei welcher Pizza erhältst du mehr Pizza für dein Geld?
A = π · r²
= π · 10²
= 314,16 (cm²)
Preis pro cm²:
A = π · r²
= π · 20²
= 1256,64 (cm²)
Preis pro cm²:
Geometrische Anwendungen
Umfang u: Die Ameise läuft außen um die Figur herum. Addiere die Teilstrecken.
Flächeninhalt A: Male die Fläche innen drin aus.
Der Radius der Halbkreise beträgt r = 1 cm, denn
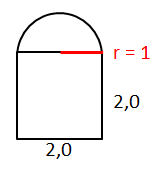
Für den Umfang läuft die Ameise an drei Seiten des Quadrates und den Halbkreisbogen entlang.
Berechne den Umfang des Halbkreises: uHalbkreis = ·uKreis = ·2·π·r = π·r
Der Flächeninhalt der Figur setzt sich zusammen aus dem Flächeninhalt des Quadrates A 1und dem Flächeninhalt des Halbreises A2.
Berechne den Flächeninhalt des Halbkreises A2 = AHalbkreis = ·AKreis = ·π·r².
Musterlösung (Schreibweisen) zu Nr. 6a:
Umfang u:
uHalbkreis = ·uKreis
= ·2·π·r
= π·r
= π·1
= 3,14 (cm)
ugesamt = 2 + 2 + 2 + 3,14 = 9,14 (cm)
Flächeninhalt A:
A1 = AQuadrat
= 2²
A2 = AHalbkreis
= ·AKreis
= ·π·r²
= ·π·1²
Agesamt = A1 + A2
= 4 + 1,57
Umfang u: Die Ameise läuft 4 Viertelkreisbögen, also um einen ganzen Kreis herum. Außerdem läuft sie viermal die Strecke vom 4cm.
Lösung: u = 41,1 cm
Flächeninhalt A: Die Fläche setzt sich zusammen aus dem Quadrat in der Mitte und 4 Viertelkreisen, also einem ganzen Kreis.
Umfang u: Das Dreieck ist ein gleichschenklig rechtwinkliges Dreieck. Die Basis ist 4cm lang. Bestimme die Länge der Schenkel mit dem Satz des Pythagoras.
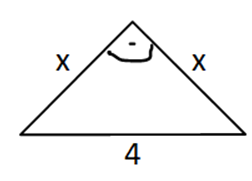
x2 + x2 = 42 &124;
2x2 = 16
…
Lösung: u = 11,9cm
Flächeninhalt A: Die Fläche setzt sich zusammen aus dem Flächeninhalt A1 des Dreiecks und dem Flächeninhalt A2 des Halbkreises.
Da das Dreieck rechtwinklig ist, sind die Schenkel je Grundseite und Höhe des Dreiecks.
Umfang u: Auch hier handelt es sich um ein gleichschenklig rechtwinkliges Dreieck. Bestimme die Schenkellänge mit dem Satz des Pythagoras (vgl. Aufgabe 6c). Der Umfang der zwei Halbkreise ist genauso groß wie der Umfang eines ganzen Kreises.
Radius r = 12:4 = 3 (cm)
Lösung: u = 35,8 (cm)
Der Winkel 45° bedeutet, dass es sich bei dem Dreieck um ein halbes Quadrat handelt. Das Dreieck ist also ebenfalls gleichschenklig rechtwinklig.
Damit beträgt der Radius des Halbkreises r = 4,5:2 = 2,25 (cm) .
Umfang u: Bestimme die Hypotenuse des Dreiecks mit dem Satz des Pythagoras.
Lösung: u = 18,0 cm (mit genauen Werten 17,9)
Berechne den Radius des Halbkreises mit dem Satz des Pythagoras.
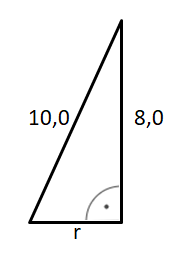
Lösung: Umfang u = 38,8cm
Flächeninhalt A: Die Grundseite des Dreiecks ist 2r lang, die Höhe beträgt 8cm. Berechne damit den Flächeninhalt des Dreiecks. Falls du die Formel nicht mehr weißt, findest du sie hinten im Schulbegleiter.
Der Umfang u setzt sich zusammen aus dem Umfang des großen Halbkreises und dem Umfang eines ganzen kleinen Kreises (zwei Halbkreise).
Lösung: u = 25,1cm
Um die Fläche der Figur zu berechnen, subtrahiere vom großen Halbkreis die zwei kleinen Halbkreise (bzw. einen ganzen kleinen Kreis).
Der Umfang der Figur ist genauso groß wie in Teil a.
Der Flächeninhalt setzt sich zusammen aus der Summe des großen Halbkreises und eines kleinen Kreises.
Der Umfang der Figur setzt sich zusammen aus dem großen Halbkreis, dem mittleren Halbkreis und zwei kleinen Halbkreisen (also einem ganzen kleinen Kreis).
Lösung: u = 25,1cm
Der Flächeninhalt der Figur setzt sich zusammen aus dem Flächeninhalt des großen Halbreises + dem Flächeninhalt des mittleren Halbkreises - zwei kleinen Halbkreisen (also einem ganzen kleinen Kreis).
Der Umfang der Figur setzt sich zusammen aus dem Umfang des großen Halbkreises und dem Umfang eines ganzen kleinen Kreises (zwei Halbkreise).
Lösung: 25,1cm
Der Flächeninhalt der Figur ist gleich dem Flächeninhalt des großen Halbkreises, denn der kleine Halbkreis wird einmal addiert und dann wieder subtrahiert.
Sachsituationen
Originallink: https://www.geogebra.org/m/krnwuf2s

Applet von Hans-Jürgen Elschenbroich
Der Flächeninhalt des Verschnittes berechnest du, indem du die Kreisflächen von der Quadratfläche subtrahierst. Bestimme für die Berechnung der Kreisflächen jeweils den Radius der Kreise.
AVerschnitt = AQuadrat - AKreise
= 80 · 80 - 1·π·40²
= 6400 - 5026,55
= 1373,45cm²
Rechne weiter für die übrigen Figuren. Was fällt dir auf?

Die Flügellänge entspricht dem Radius, die Winderntefläche der Kreisfläche.
Lösung: a) A ≈ 1122,21 m²
Die Kreisform entsteht, da die Bewässerungsanlagen sich kreisförmig drehen.
Um die ungenutzte Fläche zu berechnen, subtrahiere die Kreisfläche von der quadratischen Fläche.
Schätze die Größe des Mannes (ca. 1,80m) und damit den Durchmesser der Iris (ca. 3,20m). Berechne nun die Kreisfläche.
Berechne zunächst die Fläche des Topfbodens und die Fläche der Herdplatte.
Was ist gesucht, der Umfang oder der Flächeninhalt? Für den Umfang überlege, ob "Kalle läuft" bzw. wie in den Videos eine Ameise den Weg läuft. Für den Flächeninhalt überlege, ob du die gesuchte Größe als Fläche ausmalen könntest.
Um wie viel Prozent ... ist gefragt. Du benötigst für die Prozentrechnung also die Größen Grundwert G und Prozentwert W. Berechne diese und damit dann den Prozentsatz p%.
Erinnerung: Formel für die Prozentrechnung: Wie geht Prozentrechnung? W = G·p%. Stelle diese Formel nach p% um.
Die Größe der zweiten Pizza wird mit der der ersten Pizza verglichen. Also ist G der Flächeninhalt der ersten Pizza. W ist die Differenz der Flächeninhalte, also um welche Fläche die große Pizza größer ist also die kleine.
Du kannst auch anders vorgehen:
Berechne den Flächeninhalt der kleinen und der große Pizza. Überlege dann auf wie viel Prozent der kleinen Pizza sich die Fläche der zweiten Pizza vergrößert hat.
Gegeben sind hier also G und G+.
Berechne damit p+%.
Die Umlaufbahn ist gesucht, also der Umfang u.
Strecke: Länge der Umlaufbahn, also u.
Zeit: Der Satellit ist geostationär, er bewegt sich also genauso schnell, wie die Erde sich dreht. Für eine ganze Umlaufbahn benötigt er also 24 Stunden (einen Tag), denn die Erde dreht sich in 24 Stunde einmal um ihre Achse.
Vermischte Übungen