Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Trapez: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Navigation) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 8: | Zeile 8: | ||
===4.5) Trapez: Umfang und Flächeninhalt=== | ===4.5) Trapez: Umfang und Flächeninhalt=== | ||
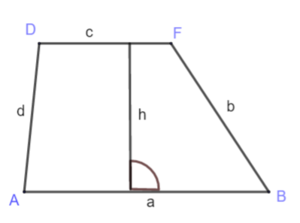
====1) Umfang und Flächeninhalt==== | |||
<ggb_applet id="M6dqPq6U" width="900" height="550" border="888888" /> | <ggb_applet id="M6dqPq6U" width="900" height="550" border="888888" /> | ||
Version vom 1. November 2020, 09:26 Uhr
4.5) Trapez: Umfang und Flächeninhalt
1) Umfang und Flächeninhalt

Umstellen nach der Seite a:
∙h |∙2
2∙A = (a+c)∙h |:h
= a+c |-c
- c = a
Stelle die Formel entsprechend nach c um.
Umstellen nach der Höhe:
∙h |∙2
2∙A = (a+c)∙h |:(a+c)
= h
Der Querschnitt des Kanals hat die Form eines Trapezes. Zeichne eine Skizze in dein Heft und beschrifte sie mit den angegebenen Maßen.
Lösung: 1386m²
Die gesamte Fläche der Backform setzt sich aus 5 Teilflächen zusammen:
Der Boden ist ein Rechteck.
Die Seiten der Backform sind jeweils Trapeze.
Skizziere die Flächen jeweils und beschrifte sie mit den angegebenen Maßen.
Zugabe von 10%
geg: G = 671cm²; p% = 10% = 0,1; p+%=110%=1,1
ges: G+
Die Fläche des Steins entspricht der Fläche des großen Rechtecks minus den 2 kleinen Trapezflächen. Zeichne eine Skizze in dein Heft und beschrifte sie vollständig. Berechne dann die Fläche eines Steines.
Bestimme damit die Anzahl der Steine pro 1m² (=10000cm²).
Lösung: AStein=265cm²; ca.38 Steine
Bestimme damit die Anzahl der Steine pro 1m² (=10000cm²).
Lösung: AStein=265cm²; ca.38 Steine