Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Gleichungen: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: Quelltext-Bearbeitung 2017
Keine Bearbeitungszusammenfassung
Markierung: Quelltext-Bearbeitung 2017
 
(20 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 20: Zeile 20:
{ Denke dir eine Zahl a aus. Addiere 4 und multipliziere das Ergebnis mit 4. Welcher Term gibt den Sachverhalt richtig an?}
{ Denke dir eine Zahl a aus. Addiere 4 und multipliziere das Ergebnis mit 4. Welcher Term gibt den Sachverhalt richtig an?}
- a·4 + a
- a·4 + a
+ 4·a + 16
+ (a+4)·4
- a
- a
- a + 4
- a + 4
Zeile 114: Zeile 114:
|-
|-
!Videos
!Videos
|NOCH ERGÄNZEN
|{{#ev:youtube|PKBC90ZwU8A|500|left}}
|-
|-
!Übungen
!Übungen
|NOCH ERGÄNZEN
|{{LearningApp|app=pzkpdnjnc20|width=80%|height=400px}}
|}
|}
<br>
<br>
Zeile 134: Zeile 134:
|-
|-
!Videos
!Videos
|NOCH ERGÄNZEN
|{{#ev:youtube|hEp3-Yp9wQo|500|left}}
|-
|-
!Übungen
!Übungen
|
|{{LearningApp|app=pidenuwjk21|width=80%|height=400px}}
|}
|}


Zeile 147: Zeile 147:
|-
|-
!Videos
!Videos
|NOCH ERGÄNZEN
|{{#ev:youtube|3-q4dvCHtVs|500|left}}
|-
|-
!Übungen
!Übungen
|NOCH ERGÄNZEN
|{{LearningApp|app=peifraewa19|width=80%|height=400px}}
|}
|}


Zeile 159: Zeile 159:
!Merksätze
!Merksätze
|{{Box|1=Gleichungen|2=Je nachdem, in welcher Potenz die Variable vorkommt, unterschieden wir zwischen verschiedenen Gleichungen.<br>
|{{Box|1=Gleichungen|2=Je nachdem, in welcher Potenz die Variable vorkommt, unterschieden wir zwischen verschiedenen Gleichungen.<br>
Lineare Gleichung: Die Variable kommt nur in einfacher Potenz vor, also x. Beispiel: 3x + 4 (x - 3) = 4 - (3 - x) + 2<br>
Lineare Gleichung: Die Variable kommt nur in einfacher Potenz vor, also x.
Quadratische Gleichung: Die Variable kommt in quadratischer Form vor, also x². Beispiel: -2x² + 2x + 24 = 0<br>
<br>Beispiel: 3x + 4 (x - 3) = 4 - (3 - x) + 2<br>
Gleichungen höheren Grades: Die Variable kommt in höherer Potenz vor. Beispiel: 375 = 3x³|3=Merksatz}}
Quadratische Gleichung: Die Variable kommt in quadratischer Form vor, also x².<br>Beispiel: -2x² + 2x + 24 = 0<br>
|-
Gleichungen höheren Grades: Die Variable kommt in höherer Potenz vor. <br>Beispiel: 375 = 3x³|3=Merksatz}}
!Videos
|
|-
|-
!Übungen
!Übungen
|{{LearningApp|app=pmy5jxe4k22|width=100%|height=400px}}
|{{LearningApp|app=pmy5jxe4k22|width=80%|height=400px}}
|}
|}
{|class=wikitable
{|class=wikitable
|-
|-
Zeile 177: Zeile 177:
|-
|-
!Video
!Video
|{{#ev:youtube|K0zma5hxJCM|800|center}}
|{{#ev:youtube|K0zma5hxJCM|500|left}}
|-
!Übungen
|
|}
|}


Zeile 191: Zeile 188:
|-
|-
!Video
!Video
|
|{{#ev:youtube|m4BcNMIZj0w|left|||start=147}}
|-
|-
!Übungen
!Übungen
Zeile 211: Zeile 208:
* Additionsverfahren (Subtraktionsverfahren)
* Additionsverfahren (Subtraktionsverfahren)
* Einsetzungsverfahren|Merksatz}}
* Einsetzungsverfahren|Merksatz}}
[[Datei:Zusammenfassung LGS.png|rahmenlos|928x928px]]
[[Datei:Anzahl der Lösungen eines LGS zeichnerisch Aufgaben vollständig.png|links|rahmenlos|958x958px]]
|-
|-
!Videos
!Videos
Zeile 227: Zeile 226:
|-
|-
!Video
!Video
|{{#ev:youtube|hBtqpqLRkg4|500|center}}
|{{#ev:youtube|hBtqpqLRkg4|500|left}}
|-
|-
!Übungen
!Übungen
|{{Box|Übung online|Bearbeite die nachfolgenden LearningApps zum Gleichsetzungsverfahren.|Üben}}
|{{Box|Übung online|Bearbeite die nachfolgenden LearningApps zum Gleichsetzungsverfahren.|Üben}}
{{LearningApp|app=ppnekev4j19|width=100%|height=400px}}
{{LearningApp|app=ppnekev4j19|width=80%|height=400px}}
{{LearningApp|app=p215ya09t20|width=100%|height=700px}}
{{LearningApp|app=p215ya09t20|width=80%|height=700px}}
|}
|}


Zeile 242: Zeile 241:
|-
|-
!Video
!Video
|{{#ev:youtube|jaEfDblkTPY|500|center}}
|{{#ev:youtube|jaEfDblkTPY|500|left}}
|-
|-
!Übungen
!Übungen
|{{Box|Übung|Bearbeite die nachfolgenden LearningApps zum Additionsverfahren.|Üben}}
|{{Box|Übung|Bearbeite die nachfolgenden LearningApps zum Additionsverfahren.|Üben}}
{{LearningApp|app=prd3sae7k19|width=100%|height=600px}}
{{LearningApp|app=prd3sae7k19|width=80%|height=600px}}
{{LearningApp|app=pq4gjoxzk20|width=100%|height=600px}}</div>
{{LearningApp|app=pq4gjoxzk20|width=80%|height=600px}}
|}
|}


Zeile 257: Zeile 256:
|-
|-
!Video
!Video
|{{#ev:youtube|oGgC7SN_Qc8|210|center}}
|{{#ev:youtube|oGgC7SN_Qc8|500|left}}
|-
|-
!Übungen
!Übungen
|{{Box|Übung online|Bearbeite die nachfolgenden LearningApps zum Einsetzungsverfahren.|Üben}}
|{{Box|Übung online|Bearbeite die nachfolgenden LearningApps zum Einsetzungsverfahren.|Üben}}
{{LearningApp|app=pcsqyrt8319|width=100%|height=600px}}
{{LearningApp|app=pcsqyrt8319|width=80%|height=600px}}
{{LearningApp|app=pmow44dsn20|width=100%|height=600px}}
{{LearningApp|app=pmow44dsn20|width=80%|height=600px}}
|}
|}




[[Datei:Zusammenfassung LGS.png|rahmenlos|928x928px]]<br>


<big>Wie viele Lösungen haben die lineare Gleichungssysteme?</big>
===2.3 Quadratische Gleichungen lösen===
<br>[[Datei:Anzahl der Lösungen eines LGS zeichnerisch Aufgaben vollständig.png|links|rahmenlos|958x958px]]
<br>


 
{|class=wikitable
===2.3 Quadratische Gleichungen lösen===
|-
{{Box|1=Formen quadratischer Gleichungen|2=Es gibt verschiedene Formen quadratischer Gleichungen und diese werden auf verschiedene Arten gelöst.
!Merksätze
|{{Box|1=Formen quadratischer Gleichungen|2=Es gibt verschiedene Formen quadratischer Gleichungen und diese werden auf verschiedene Arten gelöst.
# Rein quadratische Gleichungen: ax² + c = 0
# Rein quadratische Gleichungen: ax² + c = 0
# Gemischt quadratische Gleichungen - Normalform: x² + px + q = 0
# Gemischt quadratische Gleichungen - Normalform: x² + px + q = 0
# Gemischt quadratischer Gleichungen - allgemeine Form: ax² + bx + c = 0|3=Merksatz}}
# Gemischt quadratischer Gleichungen - allgemeine Form: ax² + bx + c = 0|3=Merksatz}}
Ordne in der nachfolgenden LearningApp, um welche Form quadratischer Gleichungen es sich handelt.
|-
{{LearningApp|app=pomp5jw8a22|width=100%|height=600px}}
!Videos
 
|Übersicht zur Lösung quadratischer Gleichungen:
 
Übersicht zur Lösung quadratischer Gleichungen:
<div class="grid">
<div class="grid">
  <div class="width-1-3">rein quadratische Gleichungen lösen
  <div class="width-1-3">rein quadratische Gleichungen lösen
Zeile 291: Zeile 286:
{{#ev:youtube|B_PtpvhnNg0|250|center}}</div>
{{#ev:youtube|B_PtpvhnNg0|250|center}}</div>
</div>
</div>
|-
!Übung
|Ordne in der nachfolgenden LearningApp, um welche Form quadratischer Gleichungen es sich handelt.
{{LearningApp|app=pomp5jw8a22|width=80%|height=600px}}
|}


{{Box|1=Rein quadratische Gleichungen lösen|2=Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:<br>
{|class=wikitable
|-
!Merksätze
|{{Box|1=Rein quadratische Gleichungen lösen|2=Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:<br>
&nbsp;&nbsp;&nbsp;&nbsp;'''ax² = c'''.<br>
&nbsp;&nbsp;&nbsp;&nbsp;'''ax² = c'''.<br>
Löse durch Wurzelziehen.|3=Merksatz}}
Löse durch Wurzelziehen.|3=Merksatz}}
Zeile 301: Zeile 305:
x<sub>1/2</sub> = ± 8<br>
x<sub>1/2</sub> = ± 8<br>
x<sub>1</sub> = -8; x<sub>2</sub> = 8<br>
x<sub>1</sub> = -8; x<sub>2</sub> = 8<br>
{{LearningApp|app=p88cbqzo320|width=100%|heigth=300px}}
|-
!Video
|{{#ev:youtube|yuoe6BN-1YQ|500|left|||start=0&end=274}}
|-
!Übung
|{{LearningApp|app=p88cbqzo320|width=80%|heigth=300px}}
|}


{{Box|1=Gemischt quadratische Gleichungen lösen mit der p-q-Formel|2=<br>
{|class=wikitable
|-
!Merksätze
|{{Box|1=Gemischt quadratische Gleichungen lösen mit der p-q-Formel|2=<br>
Damit diese Formel angewendet werden darf, muss die gemischt quadratische Gleichung in der sogenannten '''Normalform''' gegeben sein:<br>
Damit diese Formel angewendet werden darf, muss die gemischt quadratische Gleichung in der sogenannten '''Normalform''' gegeben sein:<br>
'''x² + px + q = 0'''
'''x² + px + q = 0'''
Zeile 310: Zeile 323:
Achte dabei auf die Vorzeichen von p und q.|3=Merksatz}}
Achte dabei auf die Vorzeichen von p und q.|3=Merksatz}}
{{Lösung versteckt|1=Die Struktur muss also so sein, dass die Zahl 1 der Koeffizient von x² ist (also "nichts" vor x² steht, die 1 können wir uns denken) und die andere Seite der Gleichung 0 ist. Dann ist p der Koeffizient von x (also die Zahl vor x) und q ist die Zahl ohne Variable.|2=Was muss ich für die Normalform beachten?|3=Verbergen}}
{{Lösung versteckt|1=Die Struktur muss also so sein, dass die Zahl 1 der Koeffizient von x² ist (also "nichts" vor x² steht, die 1 können wir uns denken) und die andere Seite der Gleichung 0 ist. Dann ist p der Koeffizient von x (also die Zahl vor x) und q ist die Zahl ohne Variable.|2=Was muss ich für die Normalform beachten?|3=Verbergen}}
{{Lösung versteckt|1=Präge dir die Lösungsformel ein mit dem Lied von Dorfuchs. Höre es so oft, bis es ein Ohrwurm wird:
|-
{{#ev:youtube|tRblwTsX6hQ|800|center}}|2=Lied zur Lösungsformel (Dorfuchs)|3=Verbergen}}
!Video
Übe zunächst das Umstellen der Gleichung ein die Normalform und die Bestimmung von p und q.
|{{#ev:youtube|tRblwTsX6hQ|500|left}}
{{LearningApp|app=p887tapq520|width=100%|heiht=600px}}
|-
!Übung
|Übe zunächst das Umstellen der Gleichung ein die Normalform und die Bestimmung von p und q.
{{LearningApp|app=p887tapq520|width=80%|heiht=600px}}
<br>
<br>
Beispiel:<br>
Beispiel:<br>
Zeile 328: Zeile 344:
x<sub>1/2</sub> = 11<math>\pm</math>7<br>
x<sub>1/2</sub> = 11<math>\pm</math>7<br>
x<sub>1</sub> = 18; x<sub>2</sub> = 4<br>
x<sub>1</sub> = 18; x<sub>2</sub> = 4<br>
|}


{{Box|1=Allgemein quadratische Gleichungen lösen|2=
{|class=wikitable
|-
!Merksätze
|{{Box|1=Allgemein quadratische Gleichungen lösen|2=
Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0.<br>
Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0.<br>
Im Unterschied zur Normalform ist hier der Koeffizient von x² eine beliebige Zahl a.<br>
Im Unterschied zur Normalform ist hier der Koeffizient von x² eine beliebige Zahl a.<br>
Zeile 340: Zeile 360:
x<sub>1/2</sub> = 1,25<math>\pm</math>2,75<br>
x<sub>1/2</sub> = 1,25<math>\pm</math>2,75<br>
x<sub>1</sub> = -1,5; x<sub>2</sub> = 4<br>
x<sub>1</sub> = -1,5; x<sub>2</sub> = 4<br>
|-
!Übungen
|Übe das Umwandeln in die Normalform:
{{LearningApp|app=p5ut2b9xc20|width=80%|height=400px}}
{{LearningApp|app=p581mq1hn22|width=80%|height=600px}}
|}


Übe das Umwandeln in die Normalform:
{|class=wikitable
{{LearningApp|app=p5ut2b9xc20|width=100%|height=400px}}
|-
 
!Merksätze
{{LearningApp|app=p581mq1hn22|width=100%|height=600px}}
|{{Box|1=Gemischt quadratische Gleichungen lösen durch quadratische Ergänzung|2=Hat die Gleichung die Form x² + bx + c = 0, löst du die Gleichung mithilfe der quadratischen Ergänzung:<br>
 
 
{{Lösung versteckt|1=
 
{{Box|1=Gemischt quadratische Gleichungen lösen durch quadratische Ergänzung|2=Hat die Gleichung die Form x² + bx + c = 0, löst du die Gleichung mithilfe der quadratischen Ergänzung:<br>
Stelle die Gleichung um:  x² + bx = -c.<br> Mithilfe der quadratischen Ergänzung <math>\left ( \frac{b}{2} \right )^2</math> auf beiden Seiten der Gleichung, wird dann der Term x² + bx zu einem Binom umgeformt. Dann wird auf beiden Seiten der Gleichung die Wurzel gezogen.|3=Arbeitsmethode}}
Stelle die Gleichung um:  x² + bx = -c.<br> Mithilfe der quadratischen Ergänzung <math>\left ( \frac{b}{2} \right )^2</math> auf beiden Seiten der Gleichung, wird dann der Term x² + bx zu einem Binom umgeformt. Dann wird auf beiden Seiten der Gleichung die Wurzel gezogen.|3=Arbeitsmethode}}
|-
!Video
|{{#ev:youtube|Ok73gEoo1j4|500|left}}
|-
!Übung
|{{LearningApp|app=pcse2ekgt20|width=80%|height=600px}}
{{LearningApp|app=pcse2ekgt20|width=80%|height=600px}}
|}


Schau das Video zur Beispielaufgabe an. Schreibe das Beispiel in dein Heft und mache dir Notizen zu jedem Schritt der Lösung.
{|class=wikitable
{{#ev:youtube|Ok73gEoo1j4|800|center}}
|-
<br>
!Merksätze
 
|{{Box|1=Anzahl der Lösungen quadratischer Gleichungen|2=Die Anzahl der Lösungen quadratischer Gleichungen hängt vom Radikand ab(vom Wert unter der Wurzel). Der Radikand <math>\left ( \frac{p}{2} \right )^2-q</math> wird '''Diskriminante D''' genannt.<br>Die Anzahl der Lösungen ist abhängig von D.<br>
{{LearningApp|app=pcse2ekgt20|width=100%|height=600px}}
{{LearningApp|app=pcse2ekgt20|width=100%|height=600px}}
|2=Lösen durch quadratische Ergänzung: Gleichungen der Form x² + bx + c = 0|3=Verbergen}}
 
 
{{Box|1=Anzahl der Lösungen quadratischer Gleichungen|2=Die Anzahl der Lösungen quadratischer Gleichungen hängt vom Radikand ab(vom Wert unter der Wurzel). Der Radikand <math>\left ( \frac{p}{2} \right )^2-q</math> wird '''Diskriminante D''' genannt.<br>Die Anzahl der Lösungen ist abhängig von D.<br>
Die Gleichung hat <span style="color:red">zwei</span> Lösungen, <span style="color:green">eine</span> oder <span style="color:blue">keine</span> Lösung, wenn die Diskriminante D <span style="color:red">positiv</span>, <span style="color:green">null</span> oder <span style="color:blue">negativ</span> ist.|3=Merksatz}}
Die Gleichung hat <span style="color:red">zwei</span> Lösungen, <span style="color:green">eine</span> oder <span style="color:blue">keine</span> Lösung, wenn die Diskriminante D <span style="color:red">positiv</span>, <span style="color:green">null</span> oder <span style="color:blue">negativ</span> ist.|3=Merksatz}}
Beispiele:<br>
Beispiele:<br>
<div class="grid">
<div class="grid">
Zeile 385: Zeile 407:
<math>\sqrt{-1}</math> ist nicht lösbar,  da das Quadrat einer Zahl niemals negativ ist, also die Wurzel nie aus einer negativen Zahl gezogen werden kann.</div>
<math>\sqrt{-1}</math> ist nicht lösbar,  da das Quadrat einer Zahl niemals negativ ist, also die Wurzel nie aus einer negativen Zahl gezogen werden kann.</div>
</div>
</div>
 
|-
 
!Übung
{{LearningApp|app=2626415|width=100%|height=600px}}
|{{LearningApp|app=2626415|width=80%|height=600px}}
 
 
{{Box|Übung online|Wähle Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/quadratischeGleichung.shtml '''Aufgabenfuchs'''] Nr. 1 - 19 .|Üben}}
{{Box|Übung online|Wähle Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/quadratischeGleichung.shtml '''Aufgabenfuchs'''] Nr. 1 - 19 .|Üben}}
|}

Aktuelle Version vom 26. Februar 2025, 09:22 Uhr

Schullogo HLR.jpg
zurück zur Seite der Herta-Lebenstein-Realschule


zurück zur Übersicht Vorbereitungskurs ZP 10


Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag

1. Zahlen und Größen

2. Zuordnungen und Prozent-und Zinsrechnung
3. Terme und Gleichungen (lineare Gleichungen, lineare Gleichungssysteme (LGS) und quadratische Gleichungen)
4. Funktionen: Lineare Funktionen
5. Funktionen: Quadratische Funktionen
6. Geometrie: Winkel in Figuren; Flächen- und Körperberechnungen; Pythagoras, Strahlensätze, Trigonometrie
7. Diagramme, Statistik
8. Wahrscheinlichkeitsrechnung
9. Wachstum und Exponentialfunktion

Gleichungen lösen

Einstiegstest: Terme und Gleichungen (hilfsmittelfreier Teil)

1 Denke dir eine Zahl a aus. Addiere 4 und multipliziere das Ergebnis mit 4. Welcher Term gibt den Sachverhalt richtig an?

a·4 + a
(a+4)·4
a
a + 4

2 Denke dir eine Zahl x aus. Addiere 5 und multipliziere das Ergebnis mit 6. Welcher Term gibt den Sachverhalt richtig an?

x·5 + 6
x + 6·5
6·(x + 5)
x

3 Löse die Klammer auf und fasse anschließend den Term so weit wie möglich zusammen. 4·(2 - x) + 2x?

8 - 2x
8 + 2x
8
6x

4 Löse die Gleichung: 12x - 2 = 0

x = 6
x = -6
x =
x = -

5 Löse die Gleichung: 5x - 3 = 26x

x = 7
x =
x = -7
x = -

6 Löse die Gleichung: 24x - 6 = 14 - 6x

x = 1,5
x =
x = 2,25

7 Die Summe von drei aufeinanderfolgenden natürlichen Zahlen beträgt 36. Welche Bedeutung hat n in der zugehörigen Gleichung (n-1) + n + (n+1) = 36 ?

die kleinste Zahl
die mittlere Zahl
die größte Zahl
die Summe der Zahlen

8 Wie viele Lösungen hat das lineare Gleichungssystem. (Begründe!)

I y = 3x + 5

II y = 3x + 2

unendlich viele Lösungen
eine Lösung
keine Lösung

9 Löse das lineare Gleichungssystem (ausführlich in deinem Heft). Wie lautet die Lösung?

I -2x - y = 1

II 3x + y = -1

(1|-1)
(0|1)
(0|-1)
(-1|1)

10 Löse die Gleichung (Schritt für Schritt im Heft): (x - 5)(x + 8) = 0. Wie lauten die Lösungen?

x1 = 5; x2 = -8
x1 = -5; x2 = 8
x1 = 5; x2 = -5
x1 = 8; x2 = -8

11 Löse die Gleichung (Schritt für Schritt im Heft): x² - 18x + 17. Wie lauten die Lösungen?

x1 = -18; x2 = 17
x1 = 18; x2 = -17
x1 = 17; x2 = 1
x1 = 18; x2 = 1


Auswertung des Eingangstests

Schau, welche Aufgaben du schon gut lösen konntest und bei welchen du noch Schwierigkeiten hattest. Übe dann passend.

  • Terme Nr. 1-3
  • Lineare Gleichungen Nr. 4-7
  • Lineare Gleichungssysteme Nr. 8,9
  • Quadratische Gleichungen Nr. 10,11


Übung

Löse die Aufgaben aus dem Buch und vergleiche deine Lösungen. Nutze bei Bedarf die Zusammenfassungen in diesem Lernpfad.

  • Terme: S. 147 und S. 118, P1 - P9
  • Lineare Gleichungen: S. 148 und S. 119, P10 - 19
  • Lineare Gleichungssysteme: S. 149 und S.120, P22 - P28
  • Quadratische Gleichungen: S. 151, N. 5,6 und S. 121, P35 - P37; P39-P41

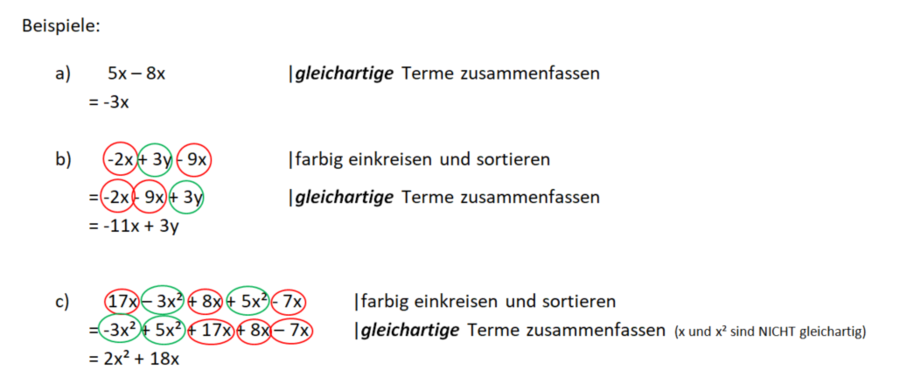
1. Terme aufstellen und zusammenfassen

Merksätze
Terme addieren und subtrahieren

Gleiche Variablen (gleichartige Terme) dürfen wir beim Addieren und Subtrahieren zusammenfassen.

Vorsicht: Unterschiedliche Variablen dürfen nicht addiert/subtrahiert werden!

Terme addieren und subtrahieren Beispiele.png

Videos
Video laden
YouTube
Übungen


Merksätze
Terme multiplizieren und dividieren

Wir dürfen beim Multiplizieren die Reihenfolge der Faktoren vertauschen. Danach multiplizieren wir die Zahlen und fassen gleiche Faktoren zu Potenzen zusammen.

Beim Dividieren durch eine Zahl dividiere nur die Zahlen.

Beispiele:
a) a∙a = a²
b) 4b∙0,2b = 4∙0,2∙b∙b = 0,8b²
c) 12x∙7y = 12∙7∙x∙y = 84xy
d) 0,5c∙3d²∙6c = 0,5∙3∙6∙c∙c∙d² = 9c²d²
e) 6ab:3b = = 2∙a (gekürzt)

Videos
Video laden
YouTube
Übungen

Merksätze
Erinnerung: Terme mit Klammern (Klasse 8)
Präge dir die Regeln zum Auflösen von Klammern ein. Notiere als Hilfe die entsprechenden Symbole hinter den Termen.

Zusammenfassung Terme mit Klammern1.png

Videos
Video laden
YouTube
Übungen


2. Gleichungen

Merksätze
Gleichungen

Je nachdem, in welcher Potenz die Variable vorkommt, unterschieden wir zwischen verschiedenen Gleichungen.
Lineare Gleichung: Die Variable kommt nur in einfacher Potenz vor, also x.
Beispiel: 3x + 4 (x - 3) = 4 - (3 - x) + 2
Quadratische Gleichung: Die Variable kommt in quadratischer Form vor, also x².
Beispiel: -2x² + 2x + 24 = 0

Gleichungen höheren Grades: Die Variable kommt in höherer Potenz vor.
Beispiel: 375 = 3x³
Übungen


Merksätze
Gleichungen lösen

Gleichungen lösen durch
Termumformungen: Klammern auflösen und Terme zusammenfassen

Äquivalenzumformungen: Auf beiden Seiten der Gleichung denselben Term addieren/subtrahieren bzw. durch dieselbe Zahl dividieren (außer 0)
Video
Video laden
YouTube


2.1 Lineare Gleichungen lösen

Merksätze
Gleichungen lösen Schritt für Schritt
Gleichungen lösen Schritt für Schritt 119.png

Video
Video laden
YouTube
Übungen
Übung online

In der nächsten Übung fasse zunächst auf beiden Seiten so weit wie möglich zusammen. Danach löse Schritt für Schritt. (Übungen von realmath)


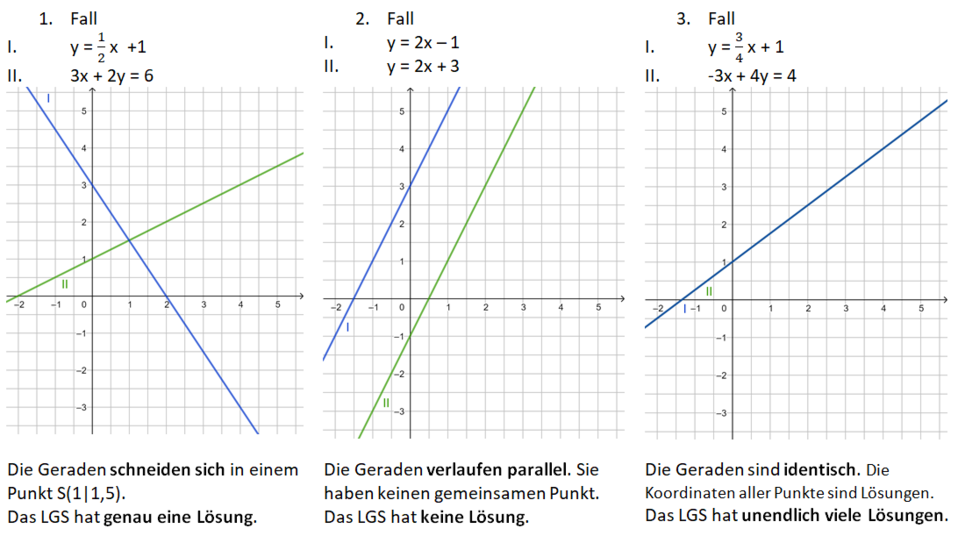
2.2 Lineare Gleichungssysteme (LGS)

Merksätze
Lineare Gleichungssysteme

Zwei lineare Gleichungen mit je zwei Variablen bilden ein lineares Gleichungssystem. Du hast verschiedene Möglichkeiten, ein LGS zu lösen:

  • zeichnerisch
  • Gleichsetzungsverfahren
  • Additionsverfahren (Subtraktionsverfahren)
  • Einsetzungsverfahren

Zusammenfassung LGS.png

Anzahl der Lösungen eines LGS zeichnerisch Aufgaben vollständig.png
Videos
Zeichnerisch lösen:
Video laden
YouTube
Gleichsetzungsverfahren:
Video laden
YouTube
Additionsverfahren:
Video laden
YouTube
Einsetzungsverfahren:
Video laden
YouTube
Merksätze
Das Gleichsetzungsverfahren
Beim Gleichsetzungsverfahren löst man beide Gleichungen nach derselben Variablen auf. Die zugehörigen Terme werden gleichgesetzt, diese Gleichung hat nur noch eine Variable.

Gleichsetzungsverfahren Schritt für Schritt.png

Video
Video laden
YouTube
Übungen
Übung online
Bearbeite die nachfolgenden LearningApps zum Gleichsetzungsverfahren.


Merksätze
Das Additionsverfahren
Beim Additionsverfahren werden die Gleichungen so umgeformt, dass beim Addieren (bzw. Subtrahieren) eine Variable wegfällt. Diese Gleichung hat nur noch eine Variable.

Additionsverfahren Schritt für Schritt berichtigt 1.png

Video
Video laden
YouTube
Übungen
Übung
Bearbeite die nachfolgenden LearningApps zum Additionsverfahren.


Merksätze
Das Einsetzungsverfahren
Beim Einsetzungsverfahren wird eine Gleichung nach einer Variablen aufgelöst. Der erhaltene Term wird dann in die andere Gleichung eingesetzt. Diese Gleichung hat nur noch eine Variable.

Einsetzungsverfahren Schritt für Schritt.png

Video
Video laden
YouTube
Übungen
Übung online
Bearbeite die nachfolgenden LearningApps zum Einsetzungsverfahren.



2.3 Quadratische Gleichungen lösen

Merksätze
Formen quadratischer Gleichungen

Es gibt verschiedene Formen quadratischer Gleichungen und diese werden auf verschiedene Arten gelöst.

  1. Rein quadratische Gleichungen: ax² + c = 0
  2. Gemischt quadratische Gleichungen - Normalform: x² + px + q = 0
  3. Gemischt quadratischer Gleichungen - allgemeine Form: ax² + bx + c = 0
Videos Übersicht zur Lösung quadratischer Gleichungen:
rein quadratische Gleichungen lösen
Video laden
YouTube
Gleichungen in der Normalform lösen mit der p-q-Formel
Video laden
YouTube
Gleichungen in allgemeiner Form lösen
Video laden
YouTube
Übung Ordne in der nachfolgenden LearningApp, um welche Form quadratischer Gleichungen es sich handelt.


Merksätze
Rein quadratische Gleichungen lösen

Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:
    ax² = c.

Löse durch Wurzelziehen.

Beispiel:
6x² + 10 = 394   |-10
6x² = 384    |:6
x² = 64    |±
x1/2 = ± 8
x1 = -8; x2 = 8

Video
Video laden
YouTube
Übung

Merksätze
Gemischt quadratische Gleichungen lösen mit der p-q-Formel


Damit diese Formel angewendet werden darf, muss die gemischt quadratische Gleichung in der sogenannten Normalform gegeben sein:
x² + px + q = 0 Dann werden die Werte für p und q bestimmt und in die Formel eingesetzt:
x1/2 = -

Achte dabei auf die Vorzeichen von p und q.
Die Struktur muss also so sein, dass die Zahl 1 der Koeffizient von x² ist (also "nichts" vor x² steht, die 1 können wir uns denken) und die andere Seite der Gleichung 0 ist. Dann ist p der Koeffizient von x (also die Zahl vor x) und q ist die Zahl ohne Variable.
Video
Video laden
YouTube
Übung Übe zunächst das Umstellen der Gleichung ein die Normalform und die Bestimmung von p und q.


Beispiel:
x² - 22x + 72 = 0  |Setze ein: p=-22; =-11; -=11; q=72
x1/2 = 11
x1/2 = 11
x1/2 = 11
x1/2 = 117
x1 = 18; x2 = 4

Kurzschreibweise:
x² - 22x + 72 = 0  |Setze ein: p=-22; =-11; -=11; q=72
x1/2 = 11
x1/2 = 117
x1 = 18; x2 = 4

Merksätze
Allgemein quadratische Gleichungen lösen

Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0.
Im Unterschied zur Normalform ist hier der Koeffizient von x² eine beliebige Zahl a.
1. Schritt: Forme in die Normalform x² + px + q = 0 um.

2. Schritt: Wende die p-q-Formel x1/2 = - an.

Beispiel:
2x² - 5x - 12 = 0   |:2 (in die Normalform umwandeln, dann p-q-Formel anwenden)
x² - 2,5x - 6 = 0  |Setze ein: p=-2,5; =1,25; -=-1,25; q=-6
x1/2 = 1,25
x1/2 = 1,252,75
x1 = -1,5; x2 = 4

Übungen Übe das Umwandeln in die Normalform:


Merksätze
Gemischt quadratische Gleichungen lösen durch quadratische Ergänzung

Hat die Gleichung die Form x² + bx + c = 0, löst du die Gleichung mithilfe der quadratischen Ergänzung:

Stelle die Gleichung um: x² + bx = -c.
Mithilfe der quadratischen Ergänzung auf beiden Seiten der Gleichung, wird dann der Term x² + bx zu einem Binom umgeformt. Dann wird auf beiden Seiten der Gleichung die Wurzel gezogen.
Video
Video laden
YouTube
Übung


Merksätze
Anzahl der Lösungen quadratischer Gleichungen

Die Anzahl der Lösungen quadratischer Gleichungen hängt vom Radikand ab(vom Wert unter der Wurzel). Der Radikand wird Diskriminante D genannt.
Die Anzahl der Lösungen ist abhängig von D.

Die Gleichung hat zwei Lösungen, eine oder keine Lösung, wenn die Diskriminante D positiv, null oder negativ ist.

Beispiele:

D > 0, zwei Lösungen:

1. x² + 6x + 5 = 0  |
x1/2 = -3
x1/2 = -3  D = 4 (positiv)
x1/2 = -32   x1 = -1 ; x2 = -5

D = 0,eine Lösung:

2. x² + 6x + 9 = 0  |
x1/2 = -3
x1/2 = -3  D = 0
x1/2 = -30

D < 0,keine Lösung:

3. x² + 6x + 10 = 0  |
x1/2 = -3
x1/2 = -3  D < 0 (negativ)

ist nicht lösbar, da das Quadrat einer Zahl niemals negativ ist, also die Wurzel nie aus einer negativen Zahl gezogen werden kann.
Übung


Übung online
Wähle Aufgaben auf der Seite Aufgabenfuchs Nr. 1 - 19 .
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Vorbereitungskurs_ZP_10_Mathematik/Gleichungen&oldid=102454“