Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Gleichungen

zurück zur Seite der Herta-Lebenstein-Realschule

zurück zur Übersicht Vorbereitungskurs ZP 10

Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag

1. Zahlen und Größen

2. Zuordnungen und Prozent-und Zinsrechnung
3. Terme und Gleichungen (lineare Gleichungen, lineare Gleichungssysteme (LGS) und quadratische Gleichungen)
4. Funktionen: Lineare Funktionen
5. Funktionen: Quadratische Funktionen
6. Geometrie: Winkel in Figuren; Flächen- und Körperberechnungen; Pythagoras, Strahlensätze, Trigonometrie
7. Diagramme, Statistik
8. Wahrscheinlichkeitsrechnung
9. Wachstum und Exponentialfunktion

Gleichungen lösen

Einstiegstest: Terme und Gleichungen (hilfsmittelfreier Teil)

1 Denke dir eine Zahl a aus. Addiere 4 und multipliziere das Ergebnis mit 4. Welcher Term gibt den Sachverhalt richtig an?

	a·4 + a
	4·a + 16
	a
	a + 4

2 Denke dir eine Zahl x aus. Addiere 5 und multipliziere das Ergebnis mit 6. Welcher Term gibt den Sachverhalt richtig an?

	x·5 + 6
	x + 6·5
	6·(x + 5)
	x

3 Löse die Klammer auf und fasse anschließend den Term so weit wie möglich zusammen. 4·(2 - x) + 2x?

	8 - 2x
	8 + 2x
	8
	6x

4 Löse die Gleichung: 12x - 2 = 0

	x = 6
	x = -6
	x = $\tfrac{1}{6}$
	x = -$\tfrac{1}{6}$

5 Löse die Gleichung: 5x - 3 = 26x

	x = 7
	x = $\tfrac{1}{7}$
	x = -7
	x = -$\tfrac{1}{7}$

6 Löse die Gleichung: 24x - 6 = 14 - 6x

	x = 1,5
	x = $\tfrac{2}{3}$
	x = 2,25

7 Die Summe von drei aufeinanderfolgenden natürlichen Zahlen beträgt 36. Welche Bedeutung hat n in der zugehörigen Gleichung (n-1) + n + (n+1) = 36 ?

	die kleinste Zahl
	die mittlere Zahl
	die größte Zahl
	die Summe der Zahlen

8 Wie viele Lösungen hat das lineare Gleichungssystem. (Begründe!)

I y = 3x + 5

II y = 3x + 2

	unendlich viele Lösungen
	eine Lösung
	keine Lösung

9 Löse das lineare Gleichungssystem (ausführlich in deinem Heft). Wie lautet die Lösung?

I -2x - y = 1

II 3x + y = -1

	(1|-1)
	(0|1)
	(0|-1)
	(-1|1)

10 Löse die Gleichung (Schritt für Schritt im Heft): (x - 5)(x + 8) = 0. Wie lauten die Lösungen?

	x1 = 5; x2 = -8
	x1 = -5; x2 = 8
	x1 = 5; x2 = -5
	x1 = 8; x2 = -8

11 Löse die Gleichung (Schritt für Schritt im Heft): x² - 18x + 17. Wie lauten die Lösungen?

	x1 = -18; x2 = 17
	x1 = 18; x2 = -17
	x1 = 17; x2 = 1
	x1 = 18; x2 = 1

Auswertung des Eingangstests

Schau, welche Aufgaben du schon gut lösen konntest und bei welchen du noch Schwierigkeiten hattest. Übe dann passend.

• Terme Nr. 1-3
• Lineare Gleichungen Nr. 4-7
• Lineare Gleichungssysteme Nr. 8,9
• Quadratische Gleichungen Nr. 10,11

Übung

Löse die Aufgaben aus dem Buch und vergleiche deine Lösungen. Nutze bei Bedarf die Zusammenfassungen in diesem Lernpfad.

• Terme: S. 147 und S. 118, P1 - P9
• Lineare Gleichungen: S. 148 und S. 119, P10 - 19
• Lineare Gleichungssysteme: S. 149 und S.120, P22 - P28
• Quadratische Gleichungen: S. 151, N. 5,6 und S. 121, P35 - P37; P39-P41

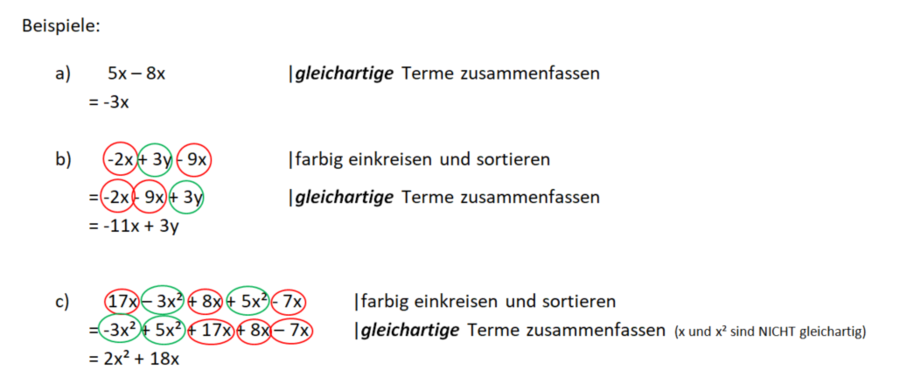
1. Terme aufstellen und zusammenfassen

Merksätze	Terme addieren und subtrahieren Gleiche Variablen (gleichartige Terme) dürfen wir beim Addieren und Subtrahieren zusammenfassen. Vorsicht: Unterschiedliche Variablen dürfen nicht addiert/subtrahiert werden!
Videos	NOCH ERGÄNZEN
Übungen	NOCH ERGÄNZEN

Merksätze	Terme multiplizieren und dividieren Wir dürfen beim Multiplizieren die Reihenfolge der Faktoren vertauschen. Danach multiplizieren wir die Zahlen und fassen gleiche Faktoren zu Potenzen zusammen. Beim Dividieren durch eine Zahl dividiere nur die Zahlen. Beispiele: a) a∙a = a² b) 4b∙0,2b = 4∙0,2∙b∙b = 0,8b² c) 12x∙7y = 12∙7∙x∙y = 84xy d) 0,5c∙3d²∙6c = 0,5∙3∙6∙c∙c∙d² = 9c²d² e) 6ab:3b = $\tfrac{6\cdot a\cdot b}{3 \cdot b}$ = 2∙a (gekürzt)
Videos	NOCH ERGÄNZEN
Übungen

Merksätze	Erinnerung: Terme mit Klammern (Klasse 8) Präge dir die Regeln zum Auflösen von Klammern ein. Notiere als Hilfe die entsprechenden Symbole hinter den Termen.
Videos	NOCH ERGÄNZEN
Übungen	NOCH ERGÄNZEN

2. Gleichungen

Merksätze	Gleichungen Je nachdem, in welcher Potenz die Variable vorkommt, unterschieden wir zwischen verschiedenen Gleichungen. Lineare Gleichung: Die Variable kommt nur in einfacher Potenz vor, also x. Beispiel: 3x + 4 (x - 3) = 4 - (3 - x) + 2 Quadratische Gleichung: Die Variable kommt in quadratischer Form vor, also x². Beispiel: -2x² + 2x + 24 = 0 Gleichungen höheren Grades: Die Variable kommt in höherer Potenz vor. Beispiel: 375 = 3x³
Videos
Übungen

Merksätze	Gleichungen lösen Gleichungen lösen durch Termumformungen: Klammern auflösen und Terme zusammenfassen Äquivalenzumformungen: Auf beiden Seiten der Gleichung denselben Term addieren/subtrahieren bzw. durch dieselbe Zahl dividieren (außer 0)
Video	Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden
Übungen

2.1 Lineare Gleichungen lösen

Merksätze	Gleichungen lösen Schritt für Schritt
Video
Übungen	Übung online In der nächsten Übung fasse zunächst auf beiden Seiten so weit wie möglich zusammen. Danach löse Schritt für Schritt. (Übungen von realmath) Übung 1 Übung 2

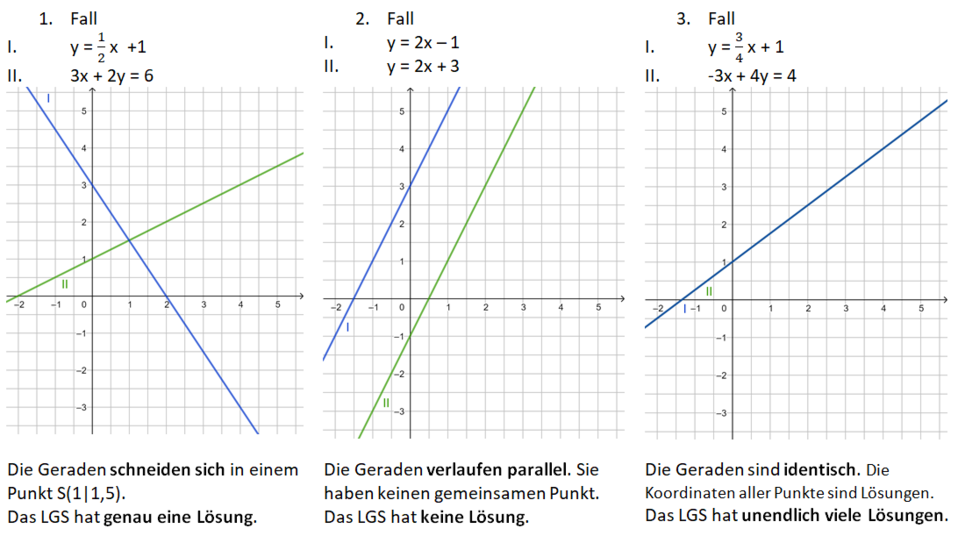
2.2 Lineare Gleichungssysteme (LGS)

Merksätze

Lineare Gleichungssysteme Zwei lineare Gleichungen mit je zwei Variablen bilden ein lineares Gleichungssystem. Du hast verschiedene Möglichkeiten, ein LGS zu lösen: zeichnerisch Gleichsetzungsverfahren Additionsverfahren (Subtraktionsverfahren) Einsetzungsverfahren

Videos

Zeichnerisch lösen: Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden Gleichsetzungsverfahren: Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden Additionsverfahren: Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden Einsetzungsverfahren: Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden

Merksätze	Das Gleichsetzungsverfahren Beim Gleichsetzungsverfahren löst man beide Gleichungen nach derselben Variablen auf. Die zugehörigen Terme werden gleichgesetzt, diese Gleichung hat nur noch eine Variable.
Video	Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden
Übungen	Übung online Bearbeite die nachfolgenden LearningApps zum Gleichsetzungsverfahren.

Merksätze	Das Additionsverfahren Beim Additionsverfahren werden die Gleichungen so umgeformt, dass beim Addieren (bzw. Subtrahieren) eine Variable wegfällt. Diese Gleichung hat nur noch eine Variable.
Video	Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden
Übungen	Übung Bearbeite die nachfolgenden LearningApps zum Additionsverfahren.

Merksätze	Das Einsetzungsverfahren Beim Einsetzungsverfahren wird eine Gleichung nach einer Variablen aufgelöst. Der erhaltene Term wird dann in die andere Gleichung eingesetzt. Diese Gleichung hat nur noch eine Variable.
Video	Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden
Übungen	Übung online Bearbeite die nachfolgenden LearningApps zum Einsetzungsverfahren.

2.3 Quadratische Gleichungen lösen

Merksätze	Formen quadratischer Gleichungen Es gibt verschiedene Formen quadratischer Gleichungen und diese werden auf verschiedene Arten gelöst. Rein quadratische Gleichungen: ax² + c = 0 Gemischt quadratische Gleichungen - Normalform: x² + px + q = 0 Gemischt quadratischer Gleichungen - allgemeine Form: ax² + bx + c = 0
Videos	Übersicht zur Lösung quadratischer Gleichungen: rein quadratische Gleichungen lösen Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden Gleichungen in der Normalform lösen mit der p-q-Formel Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden Gleichungen in allgemeiner Form lösen Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden
Übung	Ordne in der nachfolgenden LearningApp, um welche Form quadratischer Gleichungen es sich handelt.

Merksätze	Rein quadratische Gleichungen lösen Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:     ax² = c. Löse durch Wurzelziehen. Beispiel: 6x² + 10 = 394   |-10 6x² = 384    |:6 x² = 64    |±$\surd$ x1/2 = ± 8 x1 = -8; x2 = 8
Video
Übung	} Merksätze Gemischt quadratische Gleichungen lösen mit der p-q-Formel Damit diese Formel angewendet werden darf, muss die gemischt quadratische Gleichung in der sogenannten Normalform gegeben sein: x² + px + q = 0 Dann werden die Werte für p und q bestimmt und in die Formel eingesetzt: x1/2 = -$\tfrac{p}{2}\pm\sqrt{\left ( \frac{p}{2} \right )^2-q}$ Achte dabei auf die Vorzeichen von p und q. Die Struktur muss also so sein, dass die Zahl 1 der Koeffizient von x² ist (also "nichts" vor x² steht, die 1 können wir uns denken) und die andere Seite der Gleichung 0 ist. Dann ist p der Koeffizient von x (also die Zahl vor x) und q ist die Zahl ohne Variable. Video Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden Übung Übe zunächst das Umstellen der Gleichung ein die Normalform und die Bestimmung von p und q. Beispiel: x² - 22x + 72 = 0  |Setze ein: p=-22; $\tfrac{p}{2}$=-11; -$\tfrac{p}{2}$=11; q=72 x1/2 = 11$\pm\sqrt{11^2-72}$ x1/2 = 11$\pm\sqrt{121-72}$ x1/2 = 11$\pm\sqrt{49}$ x1/2 = 11$\pm$7 x1 = 18; x2 = 4 Kurzschreibweise: x² - 22x + 72 = 0  |Setze ein: p=-22; $\tfrac{p}{2}$=-11; -$\tfrac{p}{2}$=11; q=72 x1/2 = 11$\pm\sqrt{11^2-72}$ x1/2 = 11$\pm$7 x1 = 18; x2 = 4 Allgemein quadratische Gleichungen lösen Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0. Im Unterschied zur Normalform ist hier der Koeffizient von x² eine beliebige Zahl a. 1. Schritt: Forme in die Normalform x² + px + q = 0 um. 2. Schritt: Wende die p-q-Formel x1/2 = -$\tfrac{p}{2}\pm\sqrt{\left ( \frac{p}{2} \right )^2-q}$ an. Beispiel: 2x² - 5x - 12 = 0   |:2 (in die Normalform umwandeln, dann p-q-Formel anwenden) x² - 2,5x - 6 = 0  |Setze ein: p=-2,5; $\tfrac{p}{2}$=1,25; -$\tfrac{p}{2}$=-1,25; q=-6 x1/2 = 1,25$\pm\sqrt{1,25^2-(-6)}$ x1/2 = 1,25$\pm$2,75 x1 = -1,5; x2 = 4 Übe das Umwandeln in die Normalform: Gemischt quadratische Gleichungen lösen durch quadratische Ergänzung Hat die Gleichung die Form x² + bx + c = 0, löst du die Gleichung mithilfe der quadratischen Ergänzung: Stelle die Gleichung um: x² + bx = -c. Mithilfe der quadratischen Ergänzung $\left ( \frac{b}{2} \right )^2$ auf beiden Seiten der Gleichung, wird dann der Term x² + bx zu einem Binom umgeformt. Dann wird auf beiden Seiten der Gleichung die Wurzel gezogen. Schau das Video zur Beispielaufgabe an. Schreibe das Beispiel in dein Heft und mache dir Notizen zu jedem Schritt der Lösung. Video laden YouTube YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie FortfahrenAusblenden Anzahl der Lösungen quadratischer Gleichungen Die Anzahl der Lösungen quadratischer Gleichungen hängt vom Radikand ab(vom Wert unter der Wurzel). Der Radikand $\left ( \frac{p}{2} \right )^2-q$ wird Diskriminante D genannt. Die Anzahl der Lösungen ist abhängig von D. Die Gleichung hat zwei Lösungen, eine oder keine Lösung, wenn die Diskriminante D positiv, null oder negativ ist. Beispiele: D > 0, zwei Lösungen: 1. x² + 6x + 5 = 0  |$\tfrac{p}{2} = 3; q = 5$ x1/2 = -3$\pm\sqrt{3^2-5}$ x1/2 = -3$\pm\sqrt{4}$  D = 4 (positiv) x1/2 = -3$\pm$2   x1 = -1 ; x2 = -5 D = 0,eine Lösung: 2. x² + 6x + 9 = 0  |$\tfrac{p}{2} = 3; q = 9$ x1/2 = -3$\pm\sqrt{3^2-9}$ x1/2 = -3$\pm\sqrt{0}$  D = 0 x1/2 = -3$\pm$0 D < 0,keine Lösung: 3. x² + 6x + 10 = 0  |$\tfrac{p}{2} = 3; q = 10$ x1/2 = -3$\pm\sqrt{3^2-10}$ x1/2 = -3$\pm\sqrt{-1}$  D < 0 (negativ) $\sqrt{-1}$ ist nicht lösbar, da das Quadrat einer Zahl niemals negativ ist, also die Wurzel nie aus einer negativen Zahl gezogen werden kann. Übung online Wähle Aufgaben auf der Seite Aufgabenfuchs Nr. 1 - 19 .