Benutzer:Buss-Haskert/Pythagoras/Satz des Thales
1) Rechtwinklige Dreiecke zeichnen mit dem Satz des Thales
2) Satz des Pythagoras
3) Anwendungen
3.1) Anwendungen in geometrischen Figuren
3.2) Anwendungen im Raum
3.3) Anwendungen in Sachsituationen
1) Rechtwinklige Dreiecke
1.1) Rechtwinklige Dreiecke konstruieren mit dem Satz des Thales
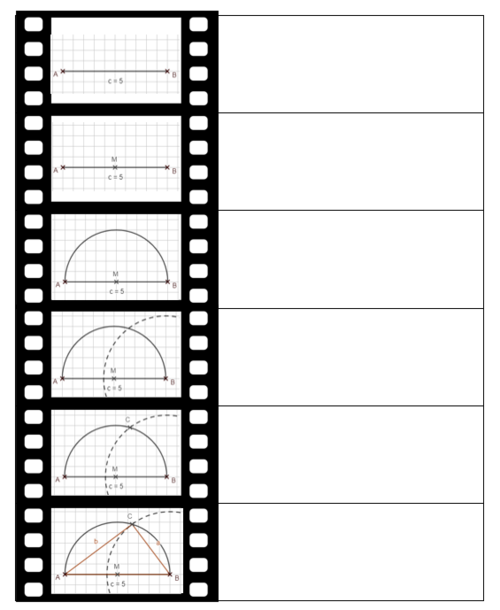
Der Satz des Pythagoras macht Aussagen über rechtwinklige Dreiecke. Der Mathematiker Thales von Milet hat herausgefunden, wie er zu einer gegebenen Grundseite alle rechtwinkligen Dreiecke zeichnen kann.
Originallink https://www.geogebra.org/m/Ncm2x9hc#material/JtndYkaP

Originallink https://www.geogebra.org/m/Ncm2x9hc#material/ndusQnFX

Originallink https://www.geogebra.org/m/Ncm2x9hc#material/rUsVUkja

(Appelt erstellt von Pöchtrager)
Orinigallink https://www.geogebra.org/m/gft4r5pm

Applet von C. Buß-Haskert
1.2) Bezeichnungen in rechtwinkligen Dreiecken
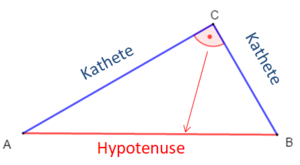
In einem rechtwinkligen Dreieck haben die Seiten besondere Namen. Diese richten sich nach ihrer Lage zum rechten Winkel.
Die längste Seite in einem rechtwinkligen Dreieck liegt immer gegenüber vom rechten Winkel. Sie heißt Hypotenuse.
Die beiden anderen Seiten heißen Katheten. Sie liegen am rechten Winkel.
In einem rechtwinkligen Dreieck heißt die längste Seite immer Hypotenuse und die anderen beiden Seiten Katheten. Die Hypotenuse liegt immer gegenüber des 90°-Winkels. Die beiden Katheten schließen immer den 90°-Winkel ein.