Benutzer:Buss-Haskert/Pythagoras/Anwendungen/Anwendungen im Raum
1) Rechtwinklige Dreiecke zeichnen mit dem Satz des Thales
2) Satz des Pythagoras
3) Anwendungen
3.1) Anwendungen in geometrischen Figuren
3.2) Anwendungen im Raum
3.3) Anwendungen in Sachsituationen
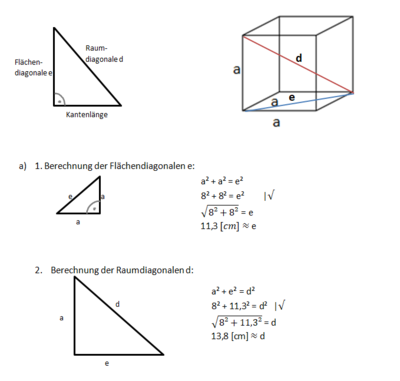
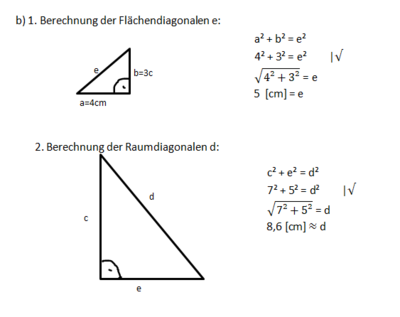
3.2 Anwendungen im Raum
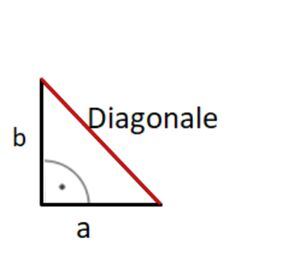
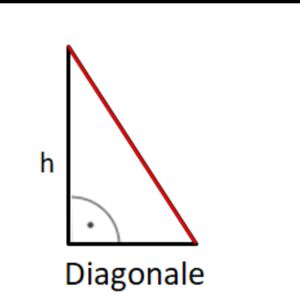
Pythagoras im Würfel und Quader
Um rechtwinklige Teildreiecke in Körpern zu erkennen, ist es hilfreich, ein Kantenmodell dieses Körpers zu erstellen. Dies kannst du basteln mit Holzspießen und Erbsen oder Weingummi.
Kantenmodell eines Würfels:
Kantenmodell eines Quaders:





Simulation zu Nr. 4 rechts: Du kannst den Würfel drehen.

Hinweise zu Pythagoras im Würfel:
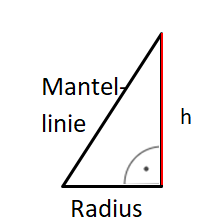
Pythagoras in der quadratischen Pyramide
Kantenmodell einer quadratischen Pyramide:


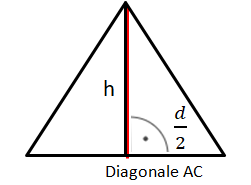
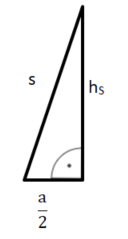
Hilfsdreieck 1: halber Parallelschnitt
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Grundseite und die Höhe der Pyramide hK. Die Hypotenuse ist die Höhe der Seitenfläche hS.
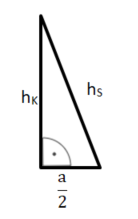
Hilfsdreieck 2: halber Seitenfläche
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Grundseite und die Höhe der Seitenfläche hS. Die Hypotenuse ist die Seitenkante s .
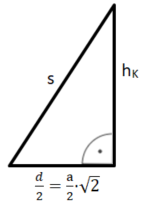
Hilfsdreieck 3: halber Diagonalschnitt
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Diagonale der Grundseite und die Höhe der Pyramide hK. Die Hypotenuse ist die Seitenkante s .
Schau die Videos zu Pythagoras in der quadratischen Pyramide an. Diese helfen dir bei der Bearbeitung der Übung 2 und 3.
Du kannst das Modell hinten im Klassenraum nutzen oder das GeoGebra-Applet: Welche rechtwinkligen Teildreiecke erkennst du? Skizziere und beschrifte!

Das Dach setzt sich aus 4 Dreiecken zusammen. ADreieck = .
Gehe schrittweise vor:
1. Berechne die Länge der Höhe ha der Seitenfläche.
2. Berechne den Flächeninhalt einer Seitenfläche (Dreieck!).
Vergleiche deine Lösungen:
Höhe der Seitenflächen ha ≈ 10,5 m
Flächeninhalt einer Seitenfläche ADreieck ≈ 40,95 m²