Benutzer:Buss-Haskert/Pythagoras/Anwendungen

zurück zur Seite der Herta-Lebenstein-Realschule

Satz des Pythagoras - Startseite

1) Rechtwinklige Dreiecke zeichnen mit dem Satz des Thales
2) Satz des Pythagoras
3) Anwendungen
   3.1) Anwendungen in geometrischen Figuren
   3.2) Anwendungen im Raum
   3.3) Anwendungen in Sachsituationen

   3.4 Anwendungen im Koordinatensystem

3) Satz des Pythagoras - Anwendungen

Der Satz des Pythagoras gilt für rechtwinklige Dreiecke. Wenn kein rechtwinkliges Dreieck vorliegt, musst du die Figur in rechtwinklige Teildreiecke zerlegen. Dann kannst du in diesen Teildreiecken fehlende Seitenlängen mit dem Satz des Pythagoras berechnen.

3.1 Anwendungen in geometrischen Figuren

Einführungsbeispiel:
Bestimme den Umfang und den Flächeninhalt des rechtwinkligen Trapezes:

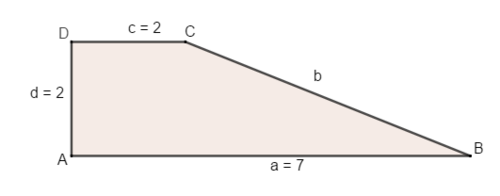
Um die Länge der Seite b zu bestimme gehe schrittweise vor:

1. Zerlege die Figur so, dass die gesuchte Seite b eine Seite in einem rechtwinkligen Dreieck ist.

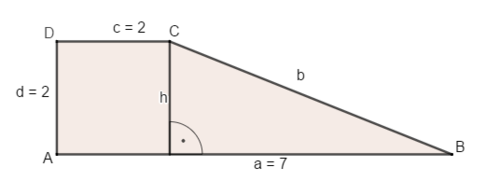
2. Überlege, ob die Seite eine Kathete oder die Hypotenuse in diesem Dreieck ist und stelle den Satz des Pythagoras richtig auf.

Die Seite b ist in dem rechtwinkligen Dreieck die Hypotenuse. Die Katheten sind h=d=2cm und 7-2 = 5 (cm) lang.

3. Berechne die Länge der Seite b mithilfe des Satzes von Pythagoras. Runde sinnvoll.

2² + 5² = b²   |$\surd$
$\sqrt{2^2+5^2}$ = b

5,4 (cm)$\approx$ b

4. Löse die Aufgabe: Berechne den Umfang und den Flächeninhalt der Figur.

Umfang u = a + b + c + d = 7 + 5,4 + 2 + 2 = 16,4 (cm)

A = $\tfrac{a+c}{2}\cdot$h = $\tfrac{7+2}{2}\cdot$2 = 9 (cm²)

Dieses Video zeigt die Berechnungen für eine symmetrisches Trapez:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

.

Übung 1

Löse die Aufgaben aus dem Buch. Achte auf eine vollständige und übersichtliche Darstellung im Heft.

• S. 114 Nr. 1
• S. 114 Nr. 2
• S. 115 Nr. 7

Hefteintrag zu Nr. 1:
Beschrifte in der Skizze die zweite Kathete im linken rechtwinkligen Dreieck mit z.B. "a".
linkes Dreieck:
15² + a² = 39²   |-15²
a² = 39² - 15²   |$\surd$
a = $\sqrt{39^2-15^2}$   (Taschenrechner)
a = 36 (cm)
rechtes Dreieck:
a² + x² = 47²
36² + x² = 47²   |-36²
x² = 47² - 36²   |$\surd$
x = $\sqrt{47^2-36^2}$   (Taschenrechner)
x $\approx$30,2 (cm)

Löse ebenso die anderen Teilaufgaben.

Übung 2

Übertrage die Skizze in dein Heft. Teile die Figuren in rechtwinklige Teildreiecke und berechne dann die fehlenden Seitenlängen.

• S. 114 Nr. 3
• S. 114 Nr. 4
• S. 114 Nr. 5
• S. 122 Nr. 4b

Teile die Figuren jeweils in ein Rechteck und ein rechtwinkliges Dreieck ein. Berechne dann mit Pythagoras die fehlenden Seitenlängen.

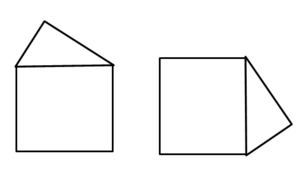
Teile die Figuren in ein Rechteck und ein rechtwinkliges Dreieck ein.

Für die Berechnung des Flächeninhaltes wiederhole die Flächeninhaltsformeln (hinten im Schulbegleiter).

Die Figuren sind jeweils Trapeze. Wiederhole die Flächeninhaltsformel für das Trapez (Schulbegleiter).

In Aufgabenteil b) handelt es sich um ein gleichschenkliges Trapez, da die benachbarten Winkel gleich groß sind. Bestimme die Höhe h mithilfe von Pythagoras.

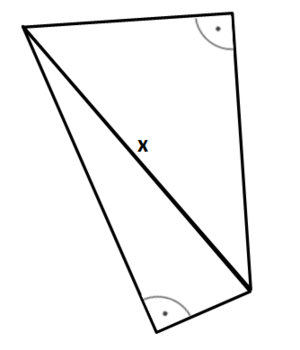
Zerlege die Figur in zwei rechtwinklige Dreiecke, indem du die Diagonale von links oben nach rechts unten zeichnest. Berechne dann zunächst die Länge der Diagonale und damit die Länge der fehlenden Seite.

Hilfsvideos zu den Aufgaben S. 114 Nr. 5 und S. 122 Nr. 4:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 3 (online)

Bearbeite die nachfolgenden Übungen. Lade einen Screenshot deiner Lösungen im Aufgaben-Modul hoch.

• Übung 1
• Übung 2

Übung 4

Übertrage die Figuren in dein Heft.Löse die Aufgaben ausführlich im Heft und prüfe deine Ergebnisse auf der Seite Aufgabenfuchs. Aufgaben:

• 22
• 26
• 29
• 42
• 47
• 48

3.2 Anwendungen im Raum