Benutzer:Buss-Haskert/Pythagoras/Anwendungen/Anwendungen in Sachsituationen

zurück zur Seite der Herta-Lebenstein-Realschule

Satz des Pythagoras - Startseite

1) Rechtwinklige Dreiecke zeichnen mit dem Satz des Thales
2) Satz des Pythagoras
3) Anwendungen
   3.1) Anwendungen in geometrischen Figuren
   3.2) Anwendungen im Raum
   3.3) Anwendungen in Sachsituationen

   3.4 Anwendungen im Koordinatensystem

3.3 Anwendungen in Sachsituationen

Anwendungsaufgaben mit dem Satz des Pythagors lösen

Um Anwendungsaufgaben mit dem Satz des Pythagoras zu lösen gehe schrittweise vor:

• Notiere die gegebenen und die gesuchte Größe.
• Erstelle eine Skizze zur Aufgabe.
• Prüfe, ob ein rechtwinkliges Dreieck vorliegt.
• Zeichne gegebenenfalls Hilfslinien, mit denen du rechtwinklige Dreiecke erzeugst.
• Wende den Satz des Pythagors im rechtwinkligen Dreieck an.
• Denke an den passenden Antwortsatz

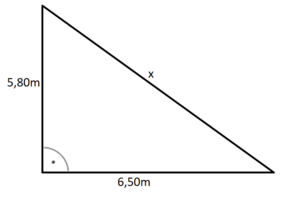
Beispiel:

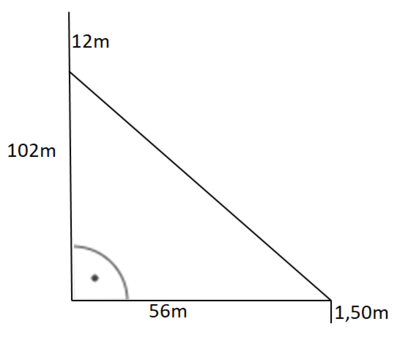
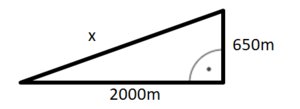
Ein Baum ist bei einem Sturm umgeknickt. Der Teil des Stammes, der noch stehengeblieben ist, ist 5,80 m hoch. Die Baumkrone berührt in einem Abstand von 6,50 m vom Stamm den Boden.

Wie hoch war der Baum?

geg: Höhe Baumstamm 5,80m; Entfernung Baumkrone zum Baumstamm 6,50m
ges: Baumhöhe

Skizze (rechtwinkliges Dreieck)

Das Dreieck ist rechtwinklig, gegeben sind die beiden Katheten, gesucht ist die Hypotenuse x.
5,8² + 6,5² = x²   |$\surd$
$\sqrt{5,8^2+6,5^2}$ = x
8,71 $\approx$ x
Der abgeknickte Teil des Baumes ist ca. 8,70 m lang.
5,80 + 8,70 = 14,50
Der Baum war also ca. 14,50 m hoch.

Übung 7

Löse die Aufgaben aus dem Buch. Beachte die nötigen Schritte bei der Lösung von Anwendungsaufgaben mit dem Satz des Pythagoras.

• S. 118 Nr. 2
• S. 118 Nr. 3
• S. 119 Nr. 9
• S. 120 Nr. 16

a) Gesucht ist die Flächendiagonale e.

b) Gesucht ist die Raumdiagonale d.

Lösungen (bunt gemischt):

2,43 m; 4,24 m; 10,3 cm; 11,1 cm; 13,2cm; ca. 61-62 m

Übung 8 (online)

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 39
• 40

Und löse die Aufgabe aus dem GeoGebra-Applet: Pythagoras in Münster.

Zeichne für jedes Seil einer Seite ein passendes Teildreieck. Das Seil ist die Hypotenuse, die Länge der Straße eine Kathete und die Höhe die andere Kathete. Du musst für die Kathetenlängen die angegebenen Werte addieren.

Diese Aufgabe entspricht der Einstiegsaufgabe bei den Anwendungsaufgaben. Denke daran, zur berechneten Länge den stehengebliebenen Teil des Baumes zu addieren.

Teile das Trapez in zwei rechtwinklige Teildreiecke und ein Rechteck ein. Bestimme so die Teilstrecken der unteren Seite und addiere zum Schluss.

Applet von M. Engel

Eine Skizze zur Aufgabe könnte so aussehen:
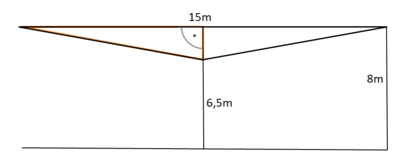Wo ist das rechtwinklige Dreieck?

Beschrifte und wende den Satz des Pythagoras an.

Das rechtwinklige Dreieck muss wie folgt beschriftet werden:

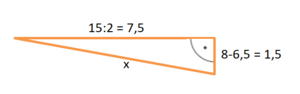
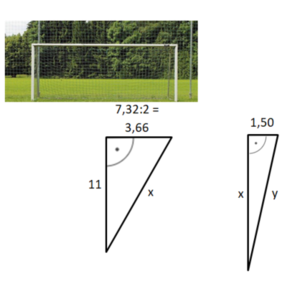
Die Hälfte der Seillänge berechnest du dann mit dem Satz des Pythagoras:
1,5² + 7,5² = x² usw.(runde auf zwei Nachkommastellen, also auf cm genau).

Das gesamte Seil muss also 15,3 m lang sein.

Übung 9

Löse die Aufgaben aus dem Buch. Beachte die nötigen Schritte bei der Lösung von Anwendungsaufgaben mit dem Satz des Pythagoras.

• S. 118 Nr. 4
• S. 118 Nr. 6
• S. 120 Nr. 17 a,b
• S. 120 Nr. 18
• S. 124 Nr. 15

Tipp zu 4b:
p% = $\tfrac{W}{G}$

W ist der Weg in Metern, den Markus sich spart, G ist die Länge des gesamten Weges (von Sven).

Tipp zu Nr. 4c:

Du hast berechnet, wie viel Meter Markus sich spart. Wenn nun beide weiterlaufen, muss jeder davon die Hälfte zurücklegen, bis sie sich treffen.

Wenn der Schrank gekippt wird, muss die Diagonale des Schrankes kleiner sein als die Raumhöhe. Achte bei der Beschriftung des Teildreiecks auf gleiche Einheiten! Prüfe nach!

a) Die längsten Strecken an den Wänden sind die Flächendiagonalen eines Quaders. Zeichne die passenden Teildreiecke und berechne.

b) Die längste Strecke im Raum ist die Raumdiagonale. Zeichne ein passendes Teildreieck (Hier ist eine Kathete eine Flächendiagonale und die andere Kathete eine Streckenlänge des Klassenzimmers).

GeoGebra-Applet zur Aufgabe Nr. 18:

Da das Pendel immer 1 m lang ist, kannst du folgendes rechtwinklige Teildreieck nutzen:

Nutze das folgende rechtwinklige Teildreieck:

Zeichne zunächst eine Skizze des Hauses und der Dachsparren. Finde dort passende rechtwinklige Teildreiecke. Zeichne dann das Teildreieck und beschrifte es. Dann kannst du den Satz des Pythagoras anwenden.

Die Folie ist im Bild grau dargestellt. Die Fläche setzt sich aus zwei Rechtecken zusammen mit einer Länge von 22m und einer Breite von 5m. Die Bahnen sind 1,50m breit und müssen sich 15cm überlappen.
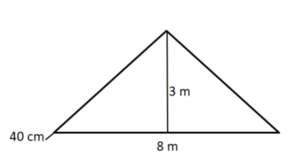
Wie viele Bahnen werden benötigt?
Wie viele Quadratmeter Folie sind das?

Vergleiche deine Lösungen zu den Aufgaben (bunt gemischt):
20cm; 80cm; 122cm; 2,34m; 5,4m; 19m; 9,9m; 9,1m; 12,6m; 38,2m; 88m; 176m
25,5%; 4 Bahnen; 264m²

1095,60 €

Übung 10

Löse die Aufgaben aus dem Buch. Beachte die nötigen Schritte bei der Lösung von Anwendungsaufgaben mit dem Satz des Pythagoras. Denke an die Skizze!

• S. 118 Nr. 5
• S. 119 Nr. 10
• S. 120 Nr. 19
• S. 120 Nr. 21 (ganz, d und e sind schwer***)
• S. 122 Nr. 9 (***)

Du musst den Satz des Pythagoras zweimal anwenden: Bestimme zunächst die Entfernung entlang des Bodens. (Skizze 1). Danach bestimmst du die Länge der Strecke, den der Ball mindestens durch die Luft zurücklegt, wenn er in 1,50m Höhe den Pfosten trifft. (Skizze 2).

Geschwindigkeit = $\tfrac{Weg}{Zeit}$; v = $\tfrac{s}{t}$
Gegeben ist die Geschwindigkeit v und die Strecke aus Teil a. Wandle die Geschwindigkeit von km/h in m/s um (:3,6).
Gesucht ist die Zeit.

Stelle die Formel nach t um und setze die Werte ein.

Der Maßstab 1:50000 bedeutet, dass 1 cm in der Karte 50000cm = 500 m in Wirklichkeit sind. Welcher Strecke entsprechen dann 4cm?

Mit diesem GeoGebra-Applet kannst du die Aufgabe 19 simulieren. Bewege die Punkte und beschreibe.

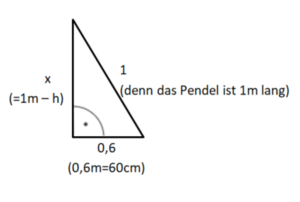
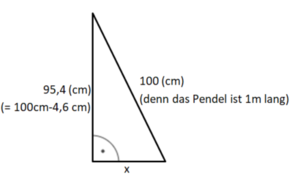
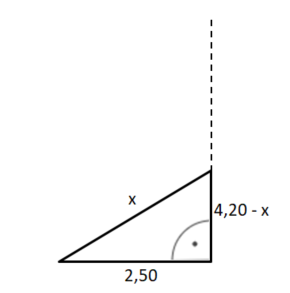
Nenne die Länge des Pendels x

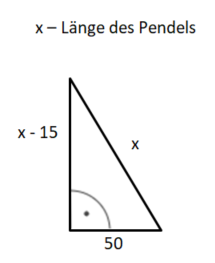
Also gilt:
(x-15)² + 50² = x²
Tipp: Löse die Klammer mit der zweiten binomische Formel auf.

Wiederholung binomische Formeln: Lernpfad Terme mit Klammern: Binomische Formeln

Löse die Gleichung:
(x-15)² + 50² = x²   |2. binomische Formel
x² - 2·x·15 + 15² + 2500 = x²
x² - 30x + 2725 = x²   | -x²
-30x + 2725 = 0   | -2725
-30x = -2725   | :(-30)

x ≈ 90,83 (cm)

Übertrage das rechtwinklige Dreieck in dein Heft.
a) Die Länge der Hypotenuse beträgt Erdradius + 45m, also 6370km + 0,045km = 6370,045km.
b) Berechne ebenso die Länge der Hypotenuse für eine Augenhöhe von 1,80m.
c) Nun ist die Länge der Kathete mit 100 Stadien = 100 ∙ 225m = 22500 m = 22,5 km gegeben und wieder die Länge der Hypotenuse gesucht. Danach subtrahiere vom Ergebnis den Erdradius.
d) Die Länge der Hypotenuse beträgt (r+h). Stelle damit den Satz des Pythagoras auf:

r² + s² = (r+h)² Löse die Klammer mit der 1. binomischen Formel auf und stelle die Gleichung nach s um.

Benenne die abgeknickten Teil des Mastes (die Hypotenuse) mit x. Wie lang sind dann die Katheten?

Vergleiche deine Lösungen (bunt gemischt):

0,47s; 91cm; 122cm; 1,36m; 11,59m; 11,69m; 40m; 2103m; 4,8km; 12,4km; 23,9km; 6370,04km

Übung 11 (Anwendungen im Raum)

Löse aus dem Buch. Skizziere die Teildreiecke!

• S. 120 Nr. 20
• S. 123 Nr. 11 (Hinweise: a) Rechne bei 11a ohne den Dachüberstand von 0,3m; b) Druckfehler: s = 6,20m)

Skizziere das Teildreieck mit der Dreieckshöhe der Grundfläche als eine Kathete und der Prismenhöhe h als zweite Kathete.

Bestimme dann zunächst die Dreieckshöhe ebenfalls mit dem Satz des Pythagoras.

Die Dachfläche besteht aus vier Dreiecken. Erinnerung: A_Dreieck = $\tfrac{g\cdot h}{2} = \tfrac{a\cdot h_a}{2}$.

Bestimme also h_a mit dem halben Parallelschnitt (s.o.)

Die Dachfläche setzt sich zusammen aus zwei Trapezen und zwei Dreiecken. Für die Flächeninhaltsformeln benötigst du die jeweiligen Höhen. Bestimme diese mit dem Satz des Pythagoras in geeigneten Teildreiecken.

(Lösung: h_Dreieck $\approx$ 5,46m; h_Trapez $\approx$ 5,76m)

Die Dachfläche setzt sich zusammen aus 4 Rechtecken, wobei jeweils zwei Rechtecke gleich groß sind. Die Länge ist immer 12,20 m. Bestimme mit dem Satz des Pythagoras die jeweilige Breite.

(Lösung:b₁ = 2,99m; b₂ = 2,60m)

Vielfältiges zusätzliches Übungsmaterial (mit Lösungen)

Vielfältiges zusätzliches Übungsmaterial mit Lösungen findest du auf der Seite Selbstlernmaterial von T. Unkelbach. Srcolle ein wenig nach unten, dort findest du Karteikartenaufgaben in leicht, mittel und schwer. Wähle aus.

3.4 Anwendungen im Koordinatensystem