Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 12: | Zeile 12: | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit|6. Wahrscheinlichkeitsrechnung]]<br>}} | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit|6. Wahrscheinlichkeitsrechnung]]<br>}} | ||
==Funktionen: | ==Funktionen== | ||
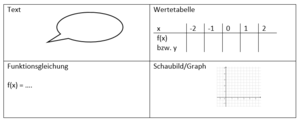
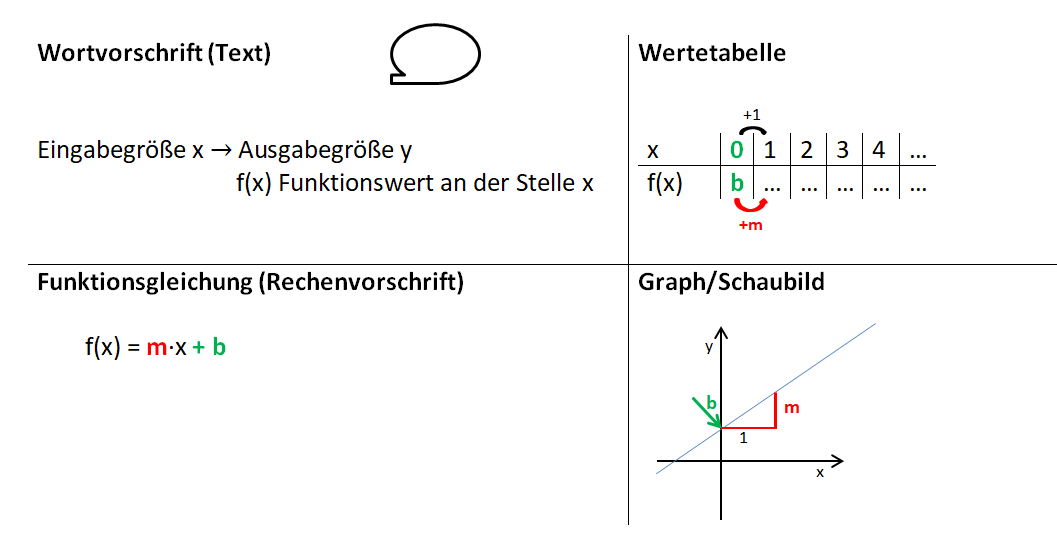
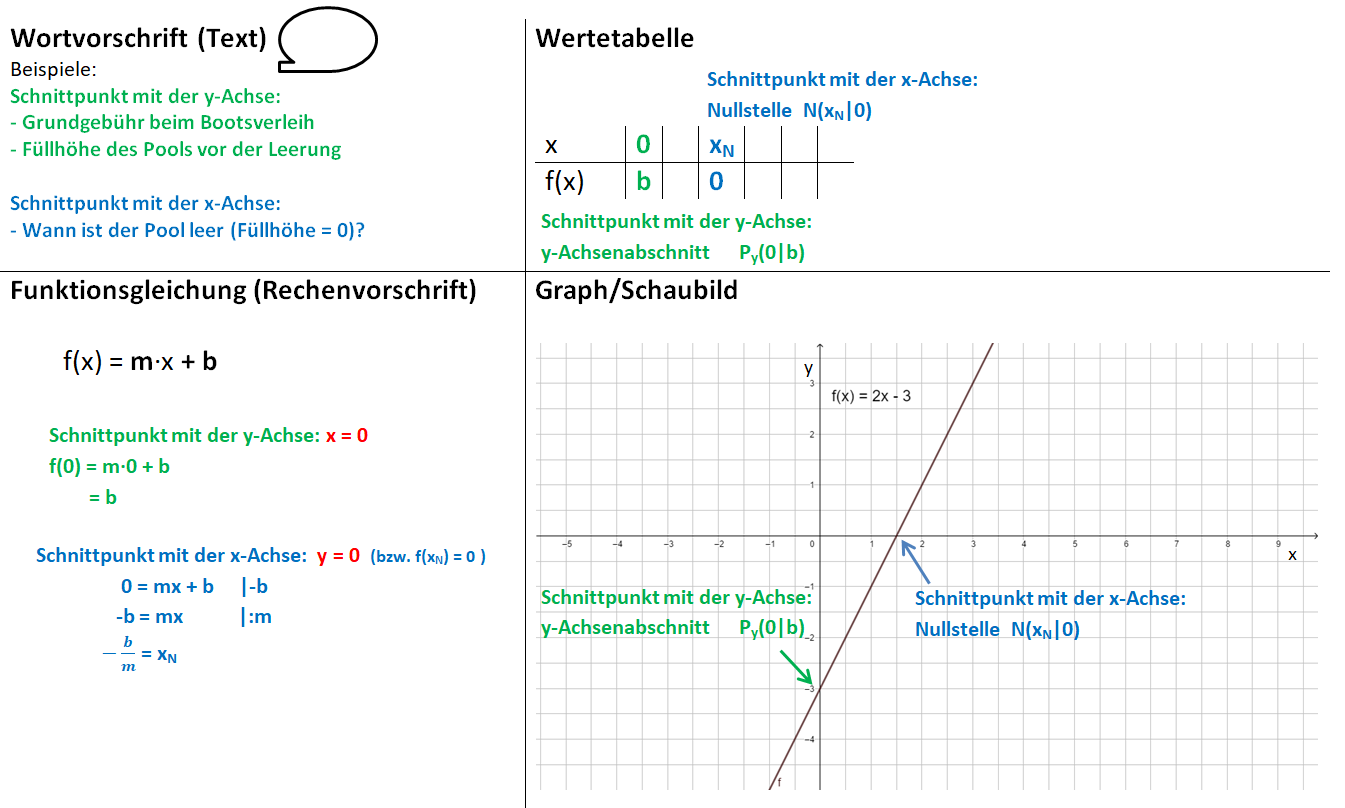
{{Box|Funktionen|[[Datei:Darstellungen von Funktionen.png|rechts|rahmenlos]]Eine Funktion ist eine eindeutige Zuordnung. Sie lässt sich auf verschiedene Arten darstellen: | |||
* als Text | |||
* als Wertetabelle | |||
* als Funktionsgleichung | |||
* als Graph|Merksatz}} | |||
{{Box|1=Funktionen|2=Orientiere dich in der [https://www.standardsicherung.schulministerium.nrw.de/cms/zentrale-pruefungen-10/faecher/getfile.php?file=2402 Formelsammlung! (S.5)]|3=Merksatz}} | |||
===Einstiegstest: '''<big>Lineare Funktionen</big>''' (hilfsmittelfreier Teil)=== | ===Einstiegstest: '''<big>Lineare Funktionen</big>''' (hilfsmittelfreier Teil)=== | ||
| Zeile 101: | Zeile 108: | ||
== | ====Lineare Funktionen erkennen==== | ||
{{Box|1=Lineare Funktionen erkennen|2=Eine Funktion, deren Funktionsgleichung die Form ''<b>f(x) = <span style="color:red>m</span>x + <span style="color:green">b</span></b>'' hat, heißt <b>lineare Funktion</b>. Der Graph einer linearen Funktion ist immer eine <b>Gerade</b> mit der <b><font color=red>Steigung m </font></b> und dem <b><font Color=green>y-Achsenabschnitt b</font></b>. Der Graph schneidet die y-Achse im Punkt P(0I<b><font Color=green>b</font></b>).<br> | {{Box|1=Lineare Funktionen erkennen|2=Eine Funktion, deren Funktionsgleichung die Form ''<b>f(x) = <span style="color:red>m</span>x + <span style="color:green">b</span></b>'' hat, heißt <b>lineare Funktion</b>. Der Graph einer linearen Funktion ist immer eine <b>Gerade</b> mit der <b><font color=red>Steigung m </font></b> und dem <b><font Color=green>y-Achsenabschnitt b</font></b>. Der Graph schneidet die y-Achse im Punkt P(0I<b><font Color=green>b</font></b>).<br> | ||
Lineare Funktionen erkennen:|3=Arbeitsmethode}} | Lineare Funktionen erkennen:|3=Arbeitsmethode}} | ||
| Zeile 213: | Zeile 211: | ||
===Lineare Funktionen: Funktionsgleichung rechnerisch bestimmen=== | ====Lineare Funktionen: Funktionsgleichung rechnerisch bestimmen==== | ||
{{Box|Lineare Funktionen: Funktionsgleichung aufstellen mithilfe der Steigung und gegebener Punkte|Du kannst die Funktionsgleichung einer linearen Funktion auch rechnerisch bestimmen: | {{Box|Lineare Funktionen: Funktionsgleichung aufstellen mithilfe der Steigung und gegebener Punkte|Du kannst die Funktionsgleichung einer linearen Funktion auch rechnerisch bestimmen: | ||
* Punkt-Steigungsform: die Steigung m und ein Punkt ist gegeben | * Punkt-Steigungsform: die Steigung m und ein Punkt ist gegeben | ||
Version vom 27. Januar 2023, 18:28 Uhr
Funktionen
Einstiegstest: Lineare Funktionen (hilfsmittelfreier Teil)
Lineare Funktionen erkennen
Diese Eigenschaften werden in folgendem Lied besungen.
Hier heißt die Funktionsgleichung f(x) = mx + n (n statt b, du findest in verschiedenen Büchern verschiedene Bezeichnungen).
Lineare Funktionen: Wertetabelle
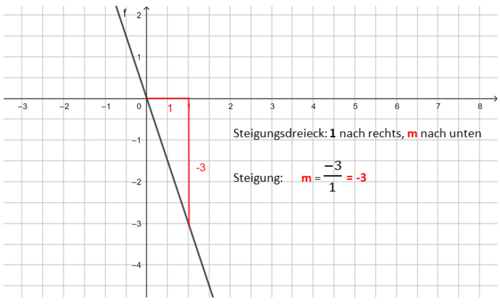
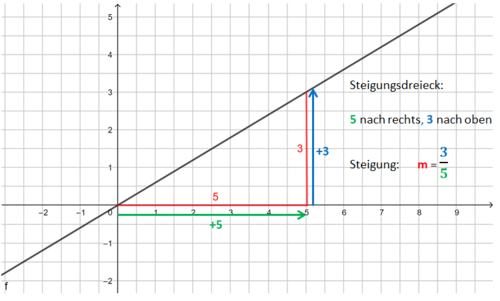
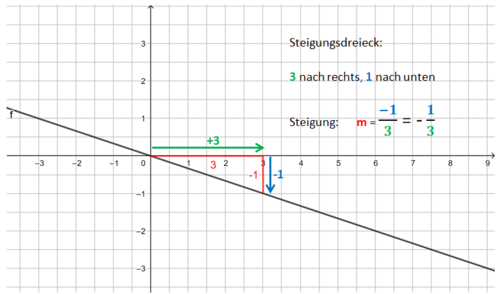
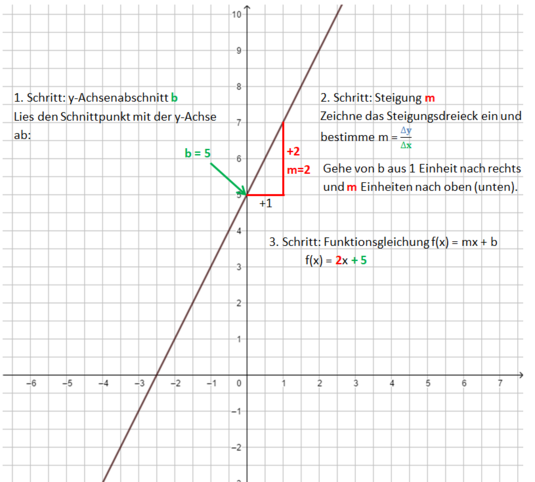
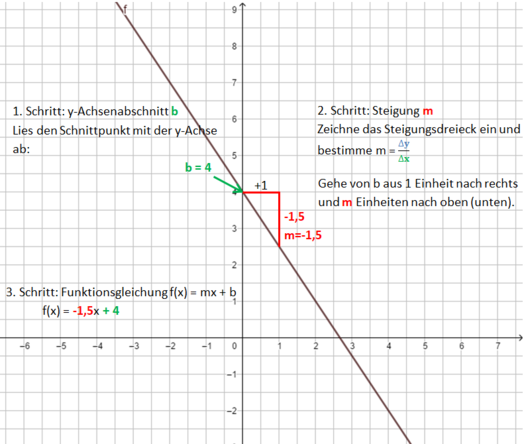
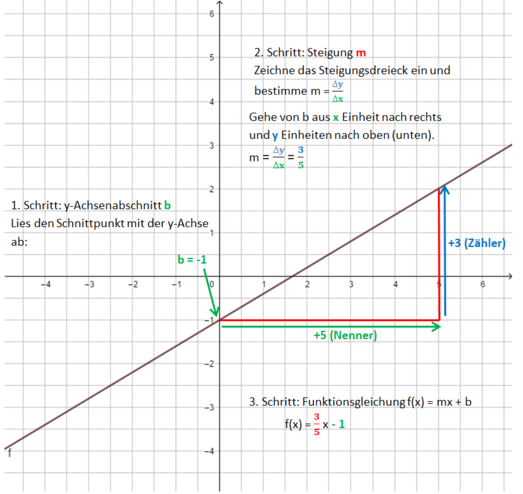
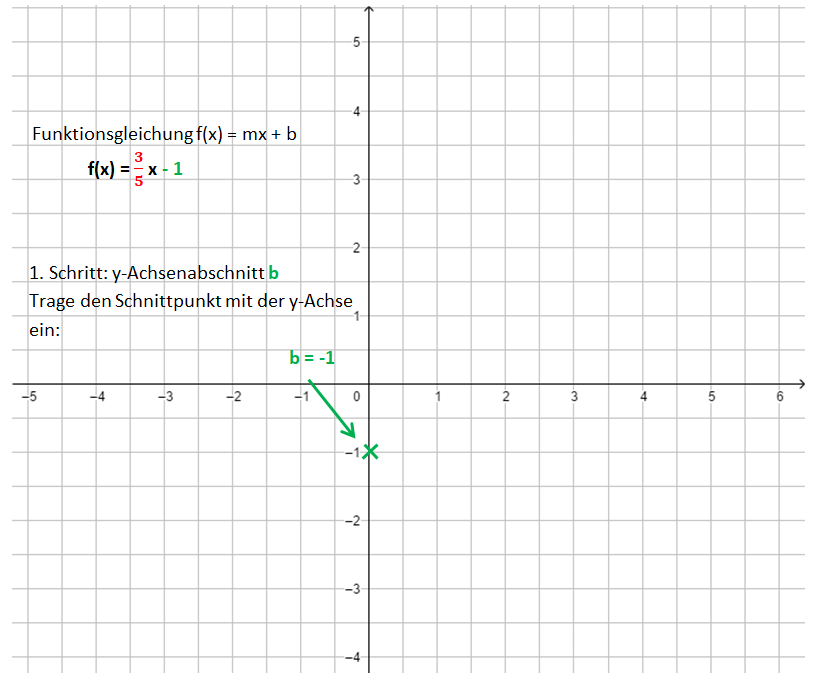
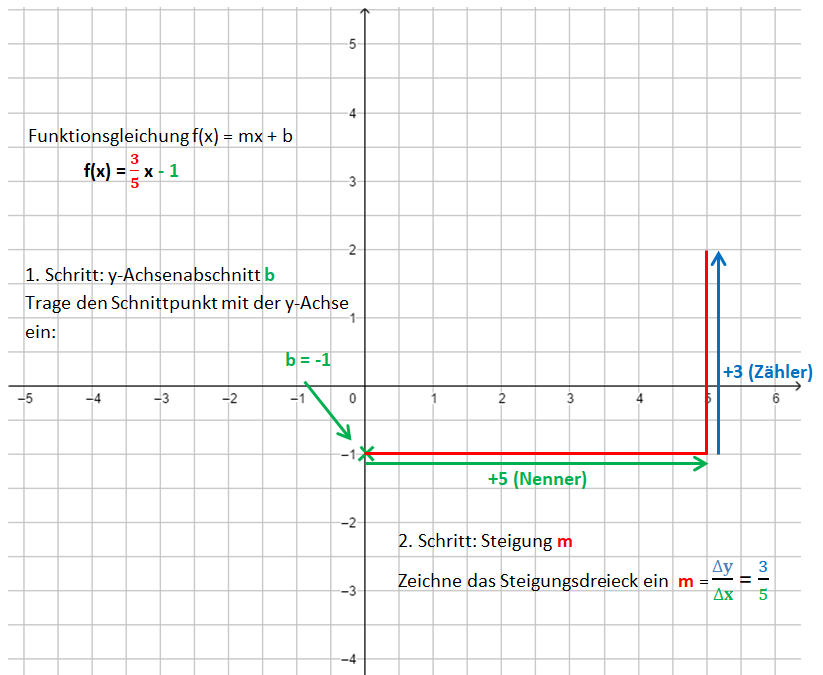
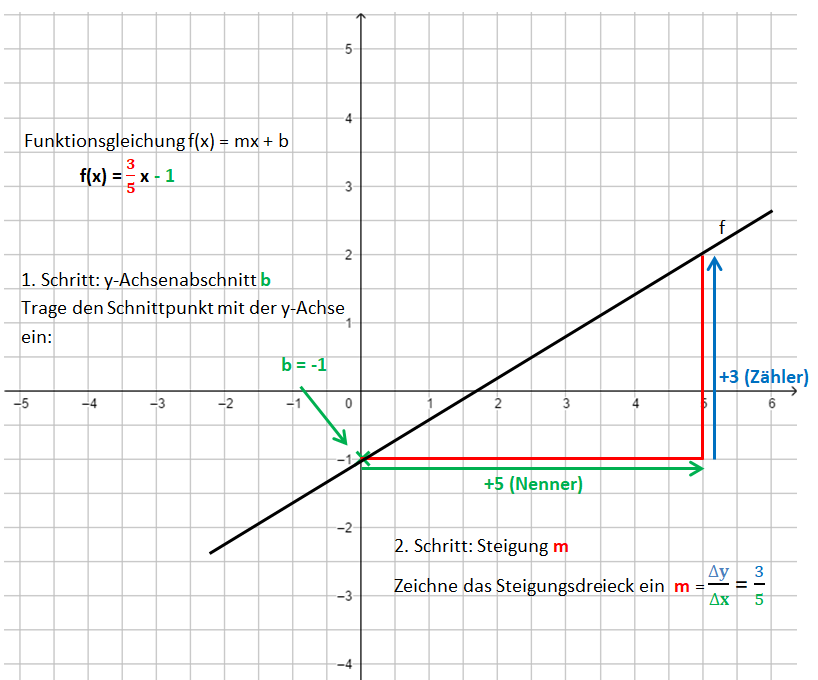
Lineare Funktionen: Gleichung und Graph
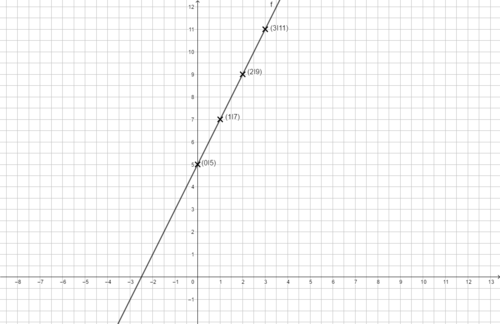
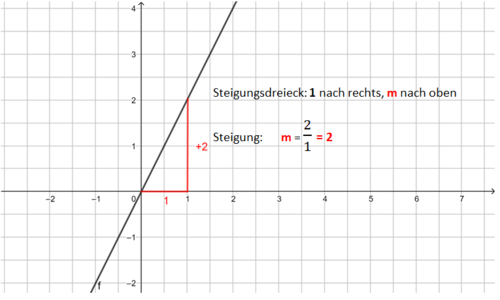
Beispiele:
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Lineare Funktionen: Funktionsgleichung rechnerisch bestimmen
Beispiel 1: Punkt-Steigungsform
geg: m = -1 und P(2|3)
ges: Funktionsgleichung der linearen Funktion
Idee: Setze m und die Koordinaten des Punktes in die Gleichung y = mx + b ein und bestimme so b.
f(x) = mx + b |m=-1 und P(2|3) einsetzen
3 = -1·2 + b |vereinfachen
3 = -2 + b |+2
5 = b
Also lautet die Funktionsgleichung f(x) = -1x + 5.
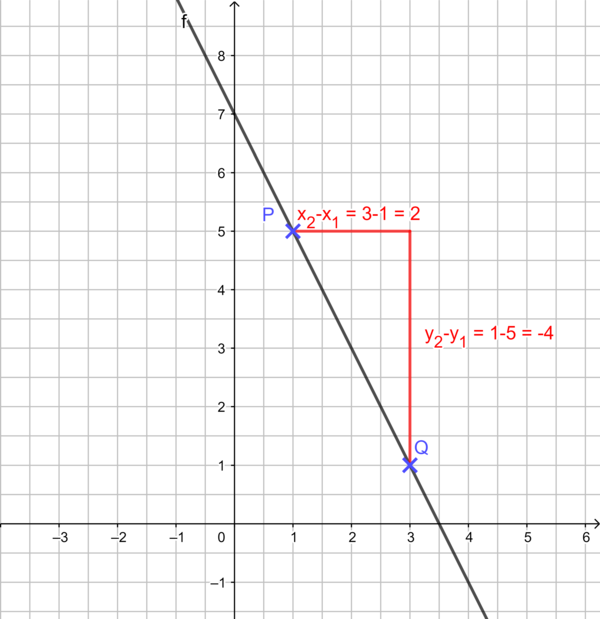
Beispiel 2: Zwei-Punkte-Form
geg: P(1|5) und Q(3|1)
ges: Funktionsgleichung der linearen Funktion
Bestimme die Steiung m: m = = = = -2
Bestimme b durch Einsetzen von m und einem der Punkte P oder Q in die Gleichung y = mx + b.
f(x) = mx + b |m=-2 und P(1|5) einsetzen
5 = -2·1 + b |vereinfachen
5 = -2 + b |+2
7 = b
Also lautet die Funktionsgleichung f(x) = -2x + 7.
Erkläre, wie du das Steigungsdreieck zwischen den Punkten P und Q einzeichnen kannst und wie du damit die Steigung m bestimmen kannst.
Lineare Funktionen: Punktprobe
Lineare Funktionen: Nullstellen bestimmen