Benutzer:Buss-Haskert/Pythagoras/Anwendungen/Anwendungen im Raum: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 85: | Zeile 85: | ||
* 60|3=Üben}} | * 60|3=Üben}} | ||
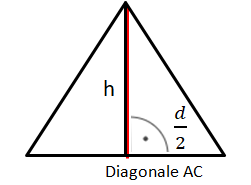
{{Lösung versteckt|Teildreieck zur Pyramide:<br> | {{Lösung versteckt|Teildreieck zur Pyramide:<br> | ||
[[Datei:Tipp zu Aufgabenfuchs Nr. 53 1.png|rahmenlos]]|Teildreieck zu Aufgabe | [[Datei:Tipp zu Aufgabenfuchs Nr. 53 1.png|rahmenlos]]|Teildreieck zu Aufgabe 55 (Pyramide)|Verbergen}} | ||
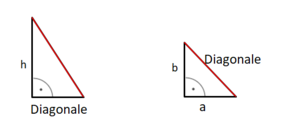
{{Lösung versteckt|Teildreieck zum Quader:<br> | {{Lösung versteckt|Teildreieck zum Quader:<br> | ||
[[Datei:Tipp zu Aufgabenfuchs Nr. 53 2.png|rahmenlos]]|Teildreiecke zu Aufgabe | [[Datei:Tipp zu Aufgabenfuchs Nr. 53 2.png|rahmenlos]]|Teildreiecke zu Aufgabe 55 (Quader)|Verbergen}} | ||
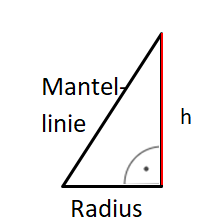
{{Lösung versteckt|Teildreieck zum Kegel:<br> | {{Lösung versteckt|Teildreieck zum Kegel:<br> | ||
[[Datei:Tipp zu Aufgabenfuchs Nr. 53 3.png|rahmenlos]]|Teildreieck zu Aufgabe | [[Datei:Tipp zu Aufgabenfuchs Nr. 53 3.png|rahmenlos]]|Teildreieck zu Aufgabe 55 (Kegel)|Verbergen}} | ||
{{Lösung versteckt|Teildreieck:<br> | {{Lösung versteckt|Teildreieck:<br> | ||
[[Datei:Tipp zu Aufgabenfuchs Nr. 55.png|rahmenlos]]|Teildreieck zu Aufgabe | [[Datei:Tipp zu Aufgabenfuchs Nr. 55.png|rahmenlos]]|Teildreieck zu Aufgabe 57|Verbergen}} | ||
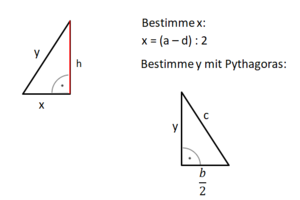
{{Lösung versteckt|Teildreiecke:<br> | {{Lösung versteckt|Teildreiecke:<br> | ||
[[Datei:Tipp zu Aufgabenfuchs Nr. 58.png|rahmenlos]]|Teildreieck zu Aufgabe | [[Datei:Tipp zu Aufgabenfuchs Nr. 58.png|rahmenlos]]|Teildreieck zu Aufgabe 60|Verbergen}} | ||
{{Fortsetzung|weiter=3.3 Anwendungen in Sachsituationen|weiterlink=Benutzer:Buss-Haskert/Pythagoras/Anwendungen/Anwendungen in Sachsituationen}} | {{Fortsetzung|weiter=3.3 Anwendungen in Sachsituationen|weiterlink=Benutzer:Buss-Haskert/Pythagoras/Anwendungen/Anwendungen in Sachsituationen}} | ||
Version vom 19. Februar 2022, 11:04 Uhr
1) Rechtwinklige Dreiecke zeichnen mit dem Satz des Thales
2) Satz des Pythagoras
3) Anwendungen
3.1) Anwendungen in geometrischen Figuren
3.2) Anwendungen im Raum
3.3) Anwendungen in Sachsituationen
3.2 Anwendungen im Raum
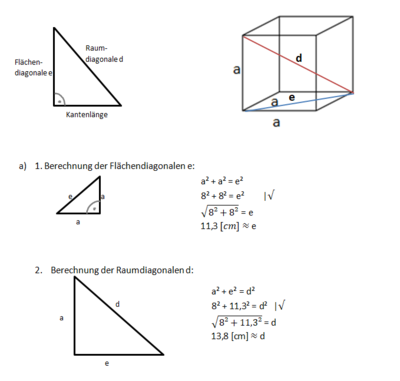
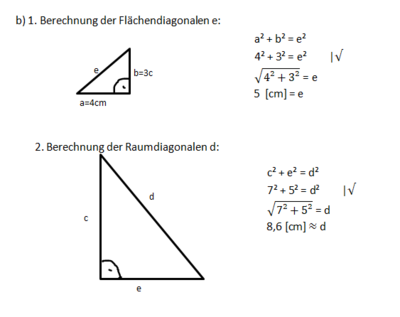
Pythagoras im Würfel und Quader
Um rechtwinklige Teildreiecke in Körpern zu erkennen, ist es hilfreich, ein Kantenmodell dieses Körpers zu erstellen. Dies kannst du basteln mit Holzspießen und Erbsen oder Weingummi.
Kantenmodell eines Würfels:
Kantenmodell eines Quaders:





Simulation zu Nr. 4 rechts: Du kannst den Würfel drehen.

Hinweise zu Pythagoras im Würfel:
Pythagoras in der quadratischen Pyramide
Kantenmodell einer quadratischen Pyramide:


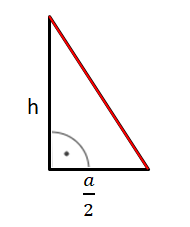
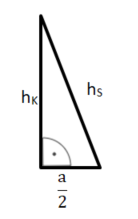
Hilfsdreieck 1: halber Parallelschnitt
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Grundseite und die Höhe der Pyramide hK. Die Hypotenuse ist die Höhe der Seitenfläche hS.
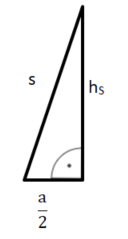
Hilfsdreieck 2: halber Seitenfläche
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Grundseite und die Höhe der Seitenfläche hS. Die Hypotenuse ist die Seitenkante s .
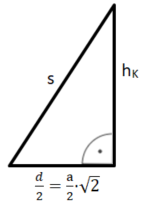
Hilfsdreieck 3: halber Diagonalschnitt
Die Katheten in diesem rechtwinkligen Dreieck sind die halbe Diagonale der Grundseite und die Höhe der Pyramide hK. Die Hypotenuse ist die Seitenkante s .
Schau die Videos zu Pythagoras in der quadratischen Pyramide an. Diese helfen dir bei der Bearbeitung der Übung 6.