Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Größen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (38 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag | Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag | ||
{{Navigation verstecken|[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | {{Navigation verstecken|[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Größen| 1. Zahlen und Größen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Zuordnungen|2. Zuordnungen und Prozent-und Zinsrechnung]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Gleichungen|3. Terme und Gleichungen (lineare Gleichungen, lineare Gleichungssysteme (LGS) und quadratische Gleichungen)]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen|4. Funktionen: Lineare Funktionen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen Teil2|5. Funktionen: Quadratische Funktionen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie|6. Geometrie: Winkel in Figuren; Flächen- und Körperberechnungen; Pythagoras, Strahlensätze, Trigonometrie]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik|7. Diagramme, Statistik]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit|8. Wahrscheinlichkeitsrechnung]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Exponentiafunktion|9. Wachstum und Exponentialfunktion]] | |||
}} | }} | ||
| Zeile 36: | Zeile 38: | ||
+ 65% > <math>\tfrac{16}{25}</math> | + 65% > <math>\tfrac{16}{25}</math> | ||
+ -<math>\tfrac{2}{5}</math> > - 0,45 | + -<math>\tfrac{2}{5}</math> > - 0,45 | ||
{Ordne die Zahlen der Größe nach. <math>\tfrac{6}{10}</math>; -0,623; -6,23; <math>\tfrac{1}{6}</math>} | |||
- -0,623 < -6,23 < <math>\tfrac{6}{10}</math> < <math>\tfrac{1}{6}</math> | |||
- -0,623 < -6,23 < <math>\tfrac{1}{6}</math> < <math>\tfrac{6}{10}</math> | |||
+ -6,23 < -0,623 < <math>\tfrac{1}{6}</math> < <math>\tfrac{6}{10}</math> | |||
- -6,23 < -0,623 < <math>\tfrac{6}{10}</math> < <math>\tfrac{1}{6}</math> | |||
{Kreuze die richtige Aussage an. <math>\sqrt{28}</math>} | |||
+ 2·<math>\sqrt{7}</math> | |||
- 7·<math>\sqrt{2}</math> | |||
- 4·<math>\sqrt{7}</math> | |||
- 2,8 | |||
{Zwischen welchen natürlichen Zahlen liegt <math>\sqrt{28}</math>?} | |||
- zwischen 4 und 5 | |||
+ zwischen 5 und 6 | |||
- zwischen 6 und 7 | |||
{Gib die Zahl ohne Zehnerpotenz an. 1,3·10<sup>-4</sup>} | |||
+ 0,00013 | |||
- 0,0013 | |||
- 0,013 | |||
- 0,13 | |||
{Welche Aussagen sind richtig? 12,5 m = ...} | {Welche Aussagen sind richtig? 12,5 m = ...} | ||
| Zeile 58: | Zeile 84: | ||
+ 65 l | + 65 l | ||
{Kreuze die richtigen Aussagen an.} | |||
+ 3 kg = 3000 g | |||
+ 1,8·10<sup>3</sup> g = 1,8 kg | |||
- 7,879 kg ≈ 8 t | |||
- 50 g = 0,5 kg | |||
{Kreuze die richtigen Aussagen an.} | |||
- 136 min = 1h 36 min | |||
+ 4,2 h = 4h 12 min | |||
- 1,5 h = 150 min | |||
+ 185 min = 3h 5min | |||
{Ein Käfer wird auf einem Foto vergrößert dargestellt. 2,5 cm auf dem Bild entsprechen 1 cm in Wirklichkeit (Maßstab 2,5:1). Wie lang ist der Käfer, wenn er auf dem Bild 6 cm misst?} | |||
- 2 cm | |||
+ 2,4 cm | |||
- 15 cm | |||
</quiz> | </quiz> | ||
{{Box|Auswertung des Eingangstests|Schau, welche Aufgaben du schon gut lösen konntest und bei welchen du noch Schwierigkeiten hattest. Übe dann passend. | {{Box|Auswertung des Eingangstests|Schau, welche Aufgaben du schon gut lösen konntest und bei welchen du noch Schwierigkeiten hattest. Übe dann passend. | ||
* Schätzen 1 | * Schätzen 1 | ||
* Zahlen runden | * Zahlen runden 2 | ||
* Bruch, Dezimalbruch, Prozent 4- | * Bruch, Dezimalbruch, Prozent 3 | ||
* | * Zahlbereiche 4-7 | ||
* ...| | * Größen 8-12 | ||
===1. | * Maßstab 13|Lösung}} | ||
{{Box|Merke: | {{Box|Übungen|Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen. | ||
* Bruch, Dezimalbruch, Prozent: S. 140 | |||
* Potenzen und Wurzeln: S. 120, P29 - S.121, P33 | |||
* Größen: S. 141 | |||
* Maßstab: S. 142, Nr. 4-7|Üben}} | |||
===1. Zahlen=== | |||
====Wiederholung Bruchrechnung==== | |||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
|*Brüche erweitern und kürzen<br> | |||
{{Box|1=Erweitern und Kürzen|2=<br> | |||
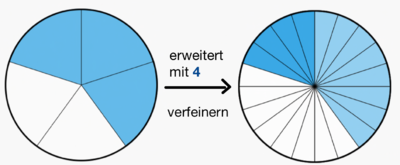
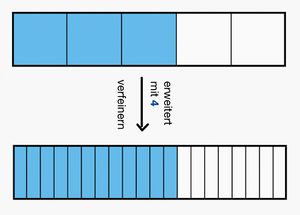
Beim <span style = "color:blue">'''Erweitern'''</span> eines Bruches werden Zähler und Nenner mit derselben Zahl multipliziert. Die Einteilung wird feiner.<br> | |||
<big> <math>\frac{3}{5}</math> = <math>\frac{3\cdot4}{5\cdot4}</math> = <math>\frac{12}{20}</math></big> <br> | |||
[[Datei:Erweitert mit 4.png|rahmenlos|400x400px]][[Datei:Erweitert mit 4 Rechteck.jpg|rahmenlos]]<br> | |||
Bruch und erweiterter Bruch haben denselben Wert. <br> | |||
<br><br> | |||
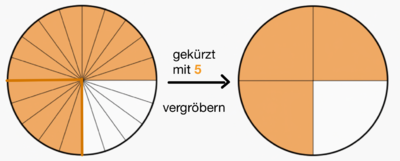
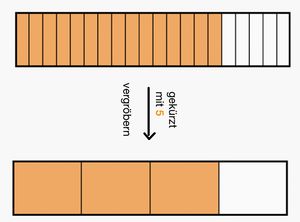
Beim <span style = "color:orange">'''Kürzen'''</span> eines Bruches werden Zähler und Nenner durch derselbe Zahl dividiert. Die Einteilung wird gröber.<br> | |||
<big> <math>\frac{15}{20} </math> = <math>\frac{15:5}{20:5} </math> = <math>\frac{3}{4}</math> </big><br> | |||
[[Datei:Kürzen mit 5.png|rahmenlos|400x400px]][[Datei:Gekürzt mit 5 Rechteck.jpg|rahmenlos]]<br> | |||
Bruch und gekürzter Bruch haben denselben Wert.|3=Merksatz}} | |||
|- | |||
!Videos | |||
|{{#ev:youtube|Q1RG-Z4jjRs|800}} | |||
{{#ev:youtube|-6OW-XImBQI|800}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=pdbonb5x522|width=85%|height=500px}} | |||
|} | |||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
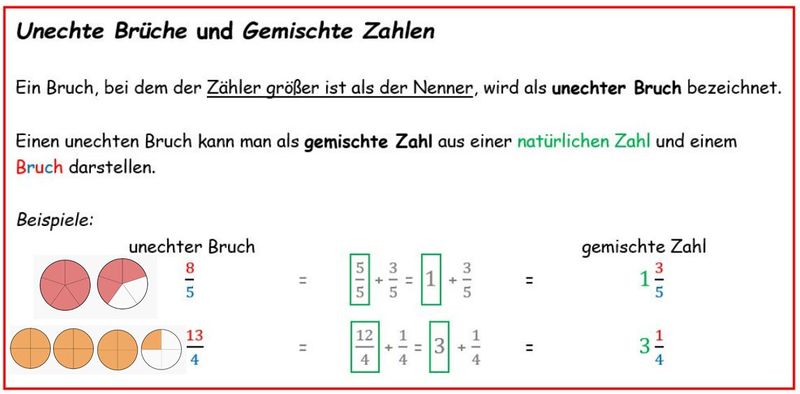
|*Brüche in gemischter Schreibweise und als unechter Bruch | |||
{{Box|Merke: ''Unechte Brüche'' und ''Gemischte Zahlen''|[[Datei:Unechte Brüche und gemischte Zahlen neu mit Bild.jpg|rahmenlos|800x800px]]|Merksatz}} | |||
|- | |||
!Video | |||
| | |||
|- | |||
!Übungen | |||
|{{Box|Übung|Bearbeite die Aufgaben auf der Seite realmath. | |||
* [https://realmath.de/Neues/Klasse6/kuerzen/gemischtezahlanvar.php gemischte Zahl - unechter Bruch]|Üben}} | |||
|} | |||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
|*Bruch, Dezimalbruch, Prozent | |||
{{Box|1=Prozentangaben in Brüche umwandeln|2=Du kannst Prozentangaben in Brüche umwandeln:<br> | |||
75% = <math>\tfrac{75}{100}</math> = <math>\tfrac{3}{4}</math><br> [[Datei:75% sind 3 4tel mit Bruchstreifen.png|rahmenlos]]<br> | |||
40% = <math>\tfrac{40}{100}</math> = <math>\tfrac{2}{5}</math><br> [[Datei:40% gleich 2 5tel mit Bruchstreifen.png|rahmenlos|300x300px]]<br> | |||
{{Box|1=Flächeneinheiten umwandeln|2=Die '''Umwandlungszahl''' bei Flächenmaßen ist <span style="color:red">'''100'''</span>. | Und nun ohne Bild: | ||
32% = <math>\tfrac{32}{100}</math> = <math>\tfrac{8}{25}</math> (gekürzt).|3=Merksatz}} | |||
{{Box|1=Brüche in Prozentangaben umwandeln|2=Und nun umgekehrt: Wandle die Brüche in Prozentangaben um. Du benötigst also den '''Nenner 100'''! <br> | |||
<div class="grid"> | |||
<div class="width-1-2"><math>\tfrac{3}{10}</math> = <math>\tfrac{30}{100}</math> = 30%<br>[[Datei:3 10er sind 30% mit Bruchstreifen.png|rahmenlos]]<br></div> | |||
<div class="width-1-2"> | |||
<math>\tfrac{7}{20}</math> = <math>\tfrac{35}{100}</math> = 35%<br> [[Datei:7 20tel sind 35% mit Bruchstreifen.png|rahmenlos]]<br></div> | |||
</div> | |||
Und nun ohne Bild: | |||
<math>\tfrac{8}{25}</math> = <math>\tfrac{32}{100}</math> = 32%.|3=Merksatz}} | |||
|- | |||
!Videos | |||
|{{#ev:youtube|MGpM8FWEzsw|800|||start=0&end=49}} | |||
{{#ev:youtube|bbjTr0YsFOs|800}} | |||
|- | |||
!Übungen | |||
| | |||
|} | |||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
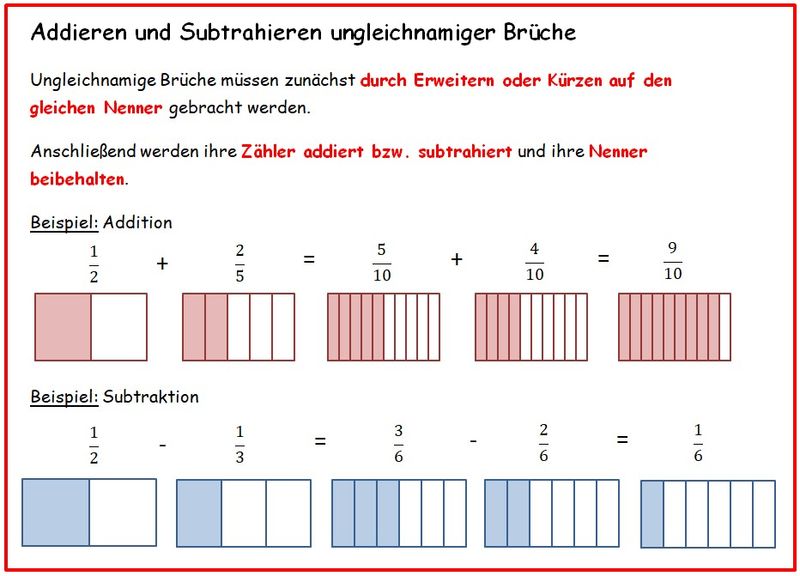
|* Brüche addieren und subtrahieren | |||
{{Box|Ungleichnamige Brüche addieren und subtrahieren|[[Datei:Merkkasten - Addieren und Subtrahieren ungleichnamiger Brüche.jpg|800x800px]]|Arbeitsmethode}} | |||
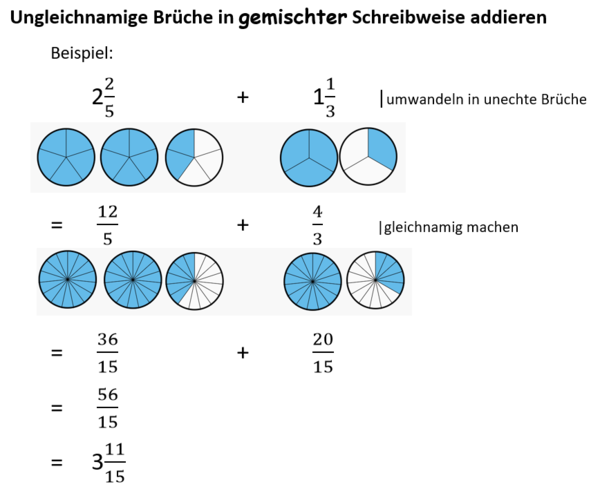
{{Box|1=Ungleichnamige Brüche in gemischter Schreibweise addieren (subtrahieren)|2=Wandle zunächst die Brüche in gemischter Schreibweise in unechte Brüche um. Dann rechnest du wie oben:<br> | |||
1. Umwandeln in die gemischte Schreibweise<br> | |||
2. Gleichnamig machen<br> | |||
3. Zähler addieren (subtrahieren), Nenner bleibt gleich<br> | |||
4. Das Ergebnis - falls möglich - kürzen und in die gemischte Schreibweise umwandeln.|3=Arbeitsmethode}} | |||
[[Datei:Ungleichnamige Brüche in gemischter Schreibweise addieren Beispiel.png|rahmenlos|600x600px]] | |||
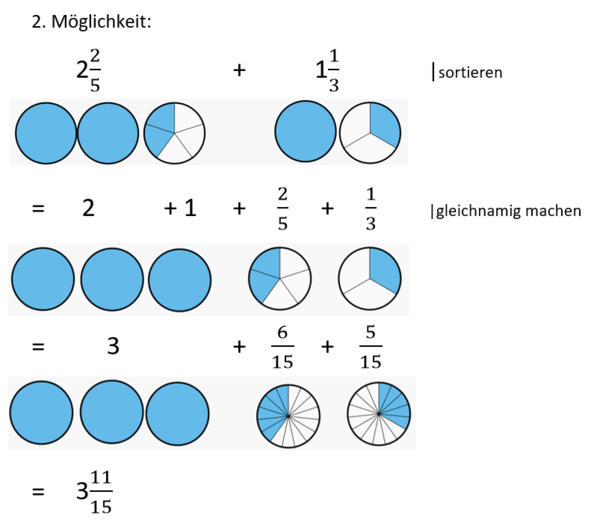
{{Lösung versteckt|[[Datei:Ungleichnamige Brüche in gemischter Schreibweise addieren 2. Möglichkeit.png|rahmenlos|600x600px]]|2. Möglichkeit|Verbergen}} | |||
{{Lösung versteckt|1=Eine weitere Möglichkeit ungleichnamige Brüche in gemischter Schreibweise zu addieren besteht darin, zuerst die Ganzen zu addieren. | |||
|2=Weitere Möglichkeit, ungleichnamige Brüche in gemischter Schreibweise zu addieren|3=Verbergen}} | |||
|- | |||
!Video | |||
|{{#ev:youtube|T3vhkqQ9CUk|800|center}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=po9v3t5vk22|width=85%|height=500px}} | |||
{{LearningApp|app=pqppe7nfc20|width=85%|height=600px}} | |||
{{LearningApp|app=pkdmmikzk22|width=85%|height=600px}} | |||
|} | |||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
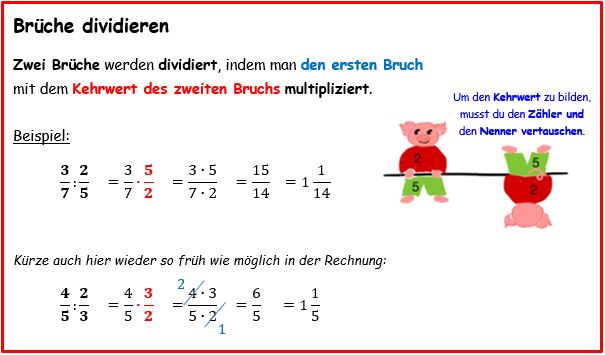
|*Brüche multiplizieren und dividieren | |||
{{Box|Hefteintrag: Brüche multiplizieren (Bruch mal Bruch)|[[Datei:Merkkasten - Brüche multiplizieren neu.jpg|800x800px]]|Arbeitsmethode}} | |||
{{Box|Hefteintrag: Brüche dividieren (Bruch durch Bruch)|[[Datei:Merkkasten neu (Lernpfad) - Brüche dividieren.jpg|800x800px]]|Arbeitsmethode}} | |||
|- | |||
!Videos | |||
|{{#ev:youtube|dYL1cta-Xnc|800}} | |||
{{#ev:youtube|FYAB-IVdJxc|800}} | |||
{{#ev:youtube|RUWu_VBRU1U|800}} | |||
{{#ev:youtube|YTdMsLPwTVY|800}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=pvx4jv12v20|width=85%|height=600px}} | |||
{{LearningApp|app=pgztwrpha20|width=85%|height=600px}} | |||
|} | |||
===2. Zahlbereiche - Potenzen und Wurzeln=== | |||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
|[[Datei:Potenzen und Wurzeln Zusammenfassung.jpg|rahmenlos|800x600px]] | |||
|- | |||
!Videos | |||
|{{#ev:youtube|DxCG0GcKhCg|800}} | |||
Die wissenschaftliche Schreibweise steht nicht auf den Zusammenfassungen: | |||
{{#ev:youtube|a3bIFKBhFow|800}} | |||
|- | |||
!Übungen | |||
|ANTON MSA Zahlbereiche | |||
|} | |||
===3.1 Größen: Längen-, Flächen- und Volumeneinheiten umwandeln=== | |||
{|class=wikitable | |||
|- | |||
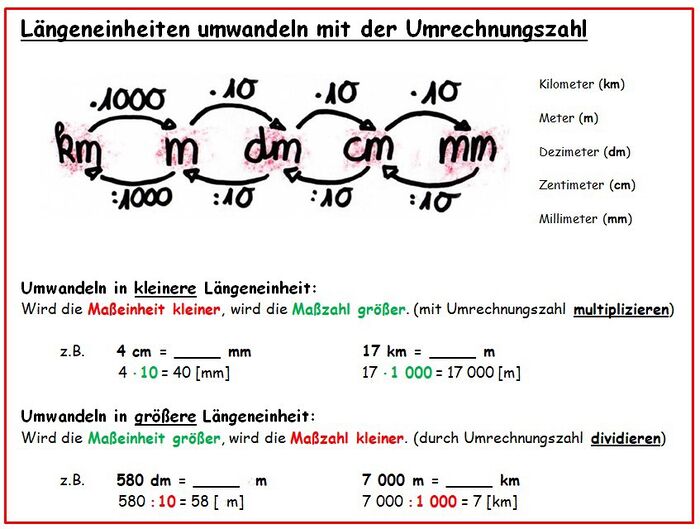
!Merksätze | |||
|{{Box|Merke: Längeneinheiten und Umrechnungszahlen|[[Datei:Merkkasten Längeneinheiten umwandeln mit Umrechnungszahl berichtigt.jpg|rahmenlos|700px]]|Merksatz}} | |||
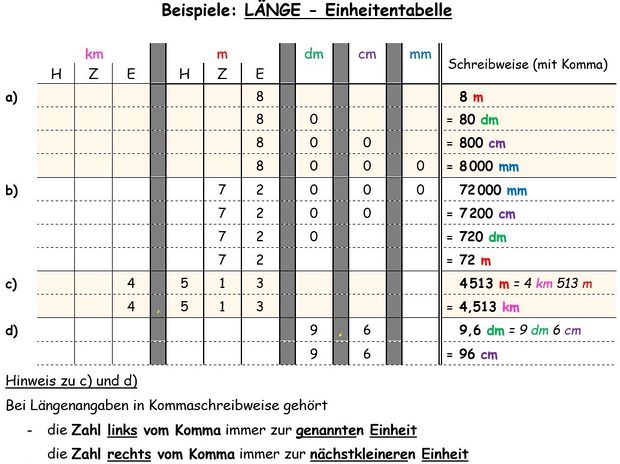
[[Datei:Länge - Einheitentabelle (Beispiele).jpg|620px]] | |||
|- | |||
!Video | |||
|{{#ev:youtube|Y5hgS2VB874|800}} | |||
|- | |||
!Übungen | |||
|{{H5p-zum|id=19572|height=560}} | |||
<small>H5P Quiz von DariaBurger</small> | |||
{{LearningApp|app=pzo1gxcrk25|85%|400px}} | |||
|} | |||
{|class=wikitable | |||
|- | |||
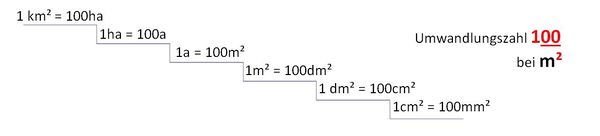
!Merksätze | |||
|{{Box|1=Flächeneinheiten umwandeln|2=Die '''Umwandlungszahl''' bei Flächenmaßen ist <span style="color:red">'''100'''</span>. | |||
[[Datei:Einheitentreppe Flächeneinheiten.jpg|rahmenlos|600x600px]]<br> | [[Datei:Einheitentreppe Flächeneinheiten.jpg|rahmenlos|600x600px]]<br> | ||
|3=Merksatz}}<br> | |3=Merksatz}}<br> | ||
|- | |||
!Video | |||
|{{#ev:youtube|0tk2CoOfHZE|800}} | |||
|- | |||
!Übungen | |||
|* [https://realmath.de/Neues/Klasse5/flaeche/umrechnung.php Übung 1] | |||
* [https://realmath.de/Neues/Klasse5/flaeche/umrechnung2.php Übung 2] | |||
* [https://realmath.de/Neues/Klasse5/flaeche/umrechnungvar.php Übung 3] | |||
|} | |||
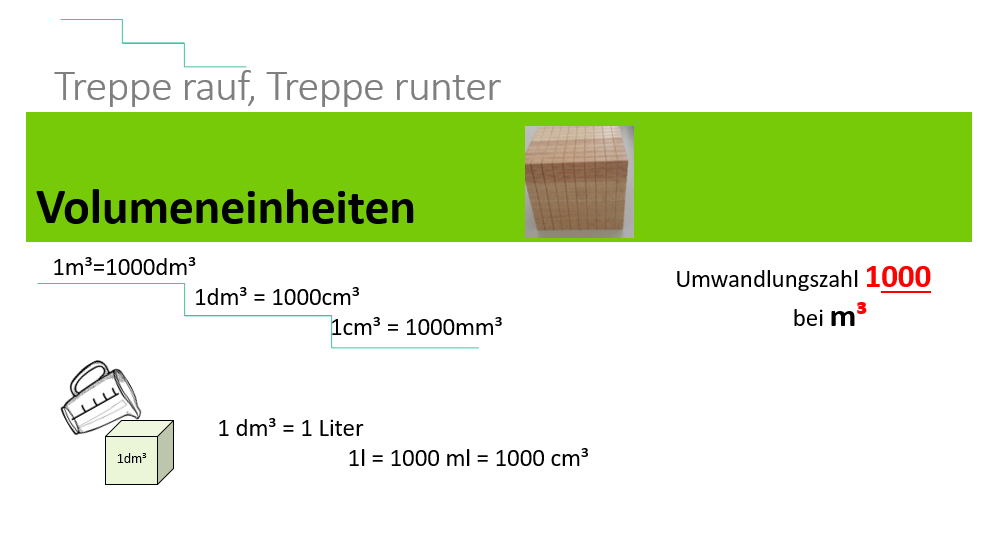
{{Box|1=Volumeneinheiten umwandeln|2=Die Umwandlungszahl bei Volumina (Rauminhalten) ist <span style="color:red">'''1000'''</span>.<br> | {|class=wikitable | ||
|- | |||
!Merksätze | |||
|{{Box|1=Volumeneinheiten umwandeln|2=Die Umwandlungszahl bei Volumina (Rauminhalten) ist <span style="color:red">'''1000'''</span>.<br> | |||
[[Datei:Volumentreppe Bild.png|rahmenlos|1000x1000px]]|3=Merksatz}} | [[Datei:Volumentreppe Bild.png|rahmenlos|1000x1000px]]|3=Merksatz}} | ||
|- | |||
!Video | |||
|{{#ev:youtube|sG5L8ogOVng|800|center}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=pk3j35acn20|width=85%|height=600px}} | |||
{{LearningApp|app=p8sesz4f520|width=85%|height=600px}} | |||
{{LearningApp|app=pbmjvj01520|width=85%|height=600px}} | |||
|} | |||
===2 | ===3.2 Größen: Maßstab=== | ||
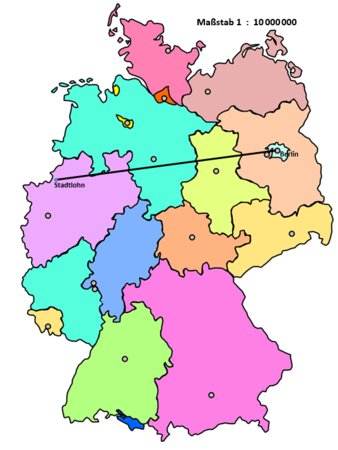
{{Box|Einstiegsaufgabe: Klassenfahrt|Die 10er Klassen der Herta-Lebenstein-Realschule fahren als Abschlussfahrt nach Berlin.<br> Wie weit ist es von Stadtlohn nach Berlin (Luftlinie), wenn du auf der Karte die Entfernung 4,5 cm misst?<br> | {{Box|Einstiegsaufgabe: Klassenfahrt|Die 10er Klassen der Herta-Lebenstein-Realschule fahren als Abschlussfahrt nach Berlin.<br> Wie weit ist es von Stadtlohn nach Berlin (Luftlinie), wenn du auf der Karte die Entfernung 4,5 cm misst?<br> | ||
| Zeile 119: | Zeile 338: | ||
===3. Gewichtseinheiten umwandeln=== | ===3.3 Größen: Gewichtseinheiten umwandeln=== | ||
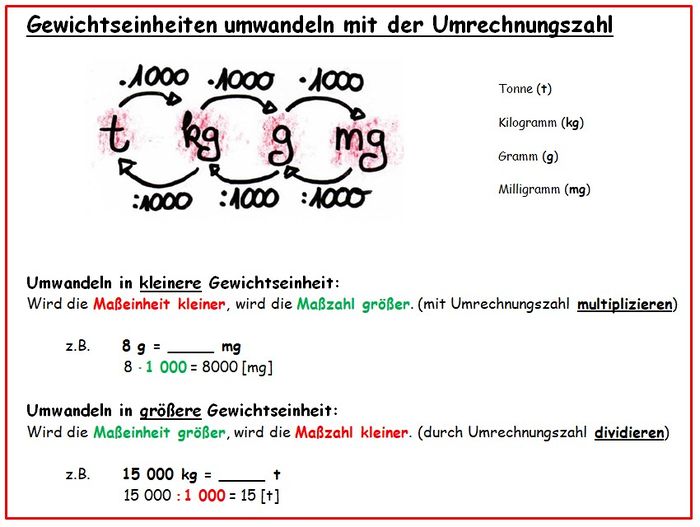
{{Box|Gewichtseinheiten und Umrechnungszahlen|[[Datei:Merkkasten Gewichtseinheiten umwandeln mit Umrechnungszahl.jpg|700px]]|Merksatz}} | {{Box|Gewichtseinheiten und Umrechnungszahlen|[[Datei:Merkkasten Gewichtseinheiten umwandeln mit Umrechnungszahl.jpg|700px]]|Merksatz}} | ||
| Zeile 125: | Zeile 344: | ||
ERGÄNZEN + Dichte | ERGÄNZEN + Dichte | ||
===4 | ===3.4 Größen: Zeiteinheiten umwandeln=== | ||
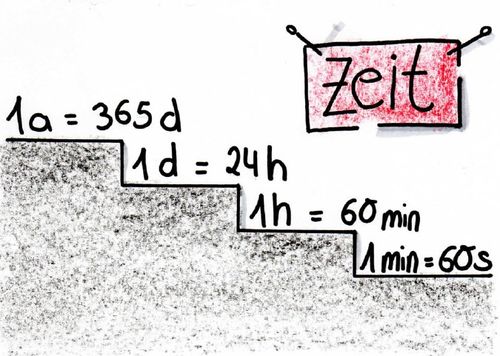
{{Box|Zeiteinheiten umwandeln|[[Datei:Zeiteinheiten umwandeln.jpg|500px]]|Merksatz}} | {{Box|Zeiteinheiten umwandeln|[[Datei:Zeiteinheiten umwandeln.jpg|500px]]|Merksatz}} | ||
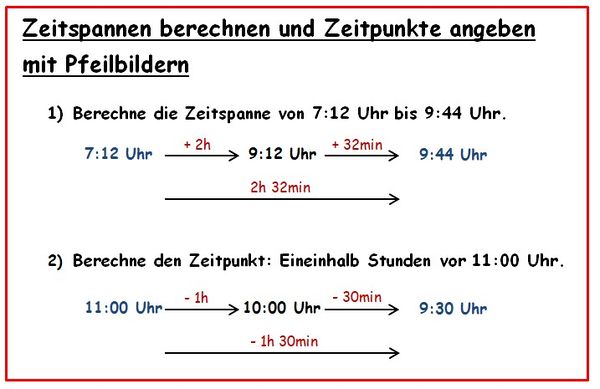
{{Box|Zeitspannen berechnen| | {{Box|Zeitspannen berechnen| | ||
[[Datei:Merkkasten Pfeilbilder.jpg|600px]]|Merksatz}} | [[Datei:Merkkasten Pfeilbilder.jpg|600px]]|Merksatz}} | ||
<br> | |||
Geschwindigkeit umwandeln | {{Box|1=Zeitangaben als Dezimalbruch umwandeln|2=Ist eine Zeitangabe als Dezimalbruch angegeben, also z.B. 0,2 Stunden, so kannst du dies auch in Minuten umwandeln, z.B. mit dem Dreisatz:<br> | ||
{{(!}} class=wikitable | |||
{{!-}} | |||
{{!}} 1 h | |||
{{!}} 60 min | |||
{{!-}} | |||
{{!}} 0,1 h | |||
{{!}} 6 min | |||
{{!-}} | |||
{{!}} 0,2 h | |||
{{!}} 12 min | |||
{{!)}} | |||
oder kurz: 0,2·60 = 12|3=Kurzinfo}} | |||
<br> | |||
{{Box|1=Geschwindigkeit v|2=Die Geschwindigkeit gibt an, welche Strecke in welcher Zeit zurückgelegt wird. Es gilt also<br> | |||
Geschwindigkeit = <math>\tfrac{Weg}{Zeit}</math><br> | |||
v = <math>\tfrac{s}{t}</math>.<br> | |||
Die Einheit der Geschwindigkeit ist <math>\tfrac{km}{h}</math> oder <math>\tfrac{m}{s}</math>.<br> | |||
Einheiten umwandeln: 25<math>\tfrac{km}{h}</math> = 25<math>\tfrac{1000m}{3600s}</math> = <math>\tfrac{25000 m}{3600 s}</math> = 6,94 <math>\tfrac{m}{s}</math><br> | |||
20<math>\tfrac{m}{s}</math> = 20·<math>\tfrac{3600 km}{1000 h}</math> = 72<math>\tfrac{km}{h}</math><br> | |||
oder kurz:<br> | |||
<math>\tfrac{km}{h}</math> → : 3,6 <math>\tfrac{m}{s}</math> | |||
<math>\tfrac{m}{s}</math> → · 3,6 <math>\tfrac{km}{h}</math>|3=Kurzinfo}} | |||
Aktuelle Version vom 28. Februar 2025, 07:16 Uhr
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag
Einstiegstest: Zahlen und Größen (hilfsmittelfreier Teil)
1. Zahlen
Wiederholung Bruchrechnung
| Merksätze | *Brüche erweitern und kürzen |
|---|---|
| Videos | |
| Übungen |
|
| Merksätze | *Brüche in gemischter Schreibweise und als unechter Bruch |
|---|---|
| Video | |
| Übungen |
| Merksätze | *Bruch, Dezimalbruch, Prozent
|
|---|---|
| Videos | |
| Übungen |
| Merksätze | * Brüche addieren und subtrahieren
Eine weitere Möglichkeit ungleichnamige Brüche in gemischter Schreibweise zu addieren besteht darin, zuerst die Ganzen zu addieren.
|
|---|---|
| Video | |
| Übungen |
|
| Merksätze | *Brüche multiplizieren und dividieren |
|---|---|
| Videos | |
| Übungen |
|
2. Zahlbereiche - Potenzen und Wurzeln
| Merksätze | 
|
|---|---|
| Videos | Die wissenschaftliche Schreibweise steht nicht auf den Zusammenfassungen: |
| Übungen | ANTON MSA Zahlbereiche |
3.1 Größen: Längen-, Flächen- und Volumeneinheiten umwandeln
| Merksätze | |
|---|---|
| Video | |
| Übungen |
H5P Quiz von DariaBurger
|
| Merksätze |
|
|---|---|
| Video | |
| Übungen | * Übung 1 |
| Merksätze | |
|---|---|
| Video | |
| Übungen |
|
3.2 Größen: Maßstab
Löse nun das Einstiegsbeispiel:

Die Entfernung zwischen Stadtlohn und Berlin beträgt also ca. 450 km Luftlinie.
Auch hier hilft dir die Tabelle weiter:
| Maßstab | Bild | Wirklichkeit |
| 4 : 1 | 4 mm | 1 mm |
| 36 mm | ? mm |
3.3 Größen: Gewichtseinheiten umwandeln
ERGÄNZEN + Dichte
3.4 Größen: Zeiteinheiten umwandeln