Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Zuordnungen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (56 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
{{Fortsetzung|vorher=zurück zur Übersicht Vorbereitungskurs ZP 10|vorherlink=Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik}}<br> | {{Fortsetzung|vorher=zurück zur Übersicht Vorbereitungskurs ZP 10|vorherlink=Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik}}<br> | ||
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag | |||
{{Navigation verstecken|[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | {{Navigation verstecken|[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Größen| 1. Zahlen und Größen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Zuordnungen|2. Zuordnungen und Prozent-und Zinsrechnung]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Gleichungen|3. Terme und Gleichungen (lineare Gleichungen, lineare Gleichungssysteme (LGS) und quadratische Gleichungen)]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen|4. Funktionen: Lineare Funktionen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen Teil2|5. Funktionen: Quadratische Funktionen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie|6. Geometrie: Winkel in Figuren; Flächen- und Körperberechnungen; Pythagoras, Strahlensätze, Trigonometrie]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik|7. Diagramme, Statistik]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit|8. Wahrscheinlichkeitsrechnung]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Exponentiafunktion|9. Wachstum und Exponentialfunktion]] | |||
}} | }} | ||
==Zuordnungen, Prozent-und Zinsrechnung== | ==Zuordnungen, Prozent-und Zinsrechnung== | ||
===Einstiegstest: '''<big>Zuordnungen, Prozent- und Zinsrechnung</big>''' (hilfsmittelfreier Teil)=== | ===Einstiegstest: '''<big>Zuordnungen, Prozent- und Zinsrechnung</big>''' (hilfsmittelfreier Teil)=== | ||
<quiz display="simple"> | |||
{ Eine zylinderförmige Vase wird gleichmäßig mit Wasser gefüllt. Welcher Graph passt? (Welche Bedeutung haben die Koordinatenachsen?) | { Eine zylinderförmige Vase wird gleichmäßig mit Wasser gefüllt. Welcher Graph passt? (Welche Bedeutung haben die Koordinatenachsen?) | ||
| Zeile 25: | Zeile 27: | ||
- D | - D | ||
{Welche Zuordnung liegt hier vor? | {Welche Zuordnung liegt hier vor? | ||
[[Datei:Tabelle ZP10 Eingangstest.png|rahmenlos]]} | |||
+ Die doppelte Anzahl kostet doppelt so viel. | |||
- Die doppelte Anzahl kostet halb so viel. | |||
- Die Wertepaare sind produktgleich. | |||
+ Das Schaubild ist eine Ursprungsgerade. | |||
+ Die Wertepaare sind quotientengleich. | |||
{Welche Aussagen gelten für proportionale Zuordnungen?} | |||
+ Wird die Eingabegröße verdoppelt, verdoppelt sich auch die Ausgabegröße. | |||
- Wird die Eingabegröße verdoppelt, halbiert sich die Ausgabegröße. | |||
+ Die Zahlenpaare sind quotientengleich. | |||
+ Der Graph ist eine Ursprungsgerade. | |||
{Welcher Graph stellt eine proportionale Zuordnung dar? | |||
{ | |||
[[Datei:Test Zuordnungen ZP10 Vorbereitung (Graphen).png|rahmenlos]]} | |||
- a | |||
+ b | |||
- c | |||
- d | |||
{ | {Welche Aussagen gelten für antiproportionale Zuordnungen?} | ||
- Wird die Eingabegröße verdoppelt, verdoppelt sich auch die Ausgabegröße. | |||
+ Wird die Eingabegröße verdoppelt, halbiert sich die Ausgabegröße. | |||
+ Die Zahlenpaare sind produktgleich. | |||
- Der Graph ist eine Ursprungsgerade. | |||
{Welcher Graph stellt eine antiproportionale Zuordnung dar? | |||
[[Datei:Test Zuordnungen ZP10 Vorbereitung (Graphen).png|rahmenlos]]} | |||
- a | |||
- b | |||
- c | |||
+ d | |||
{ | {Um eine Wand zu streichen, benötigen 4 Maler:innen 6h. Wie viel Zeit benötigen 5 Maler:innen?} | ||
- 4h 8 Minuten | |||
- 4h 28 Minuten | |||
- 4,5 h | |||
+ 4h 48 Minuten | |||
{ | {Ein 300g schweres Stück Käse kostet 6,00€. Wie viel kostet ein 450g schweres Stück der gleichen Sorte?} | ||
+ 9 € | |||
- 8 € | |||
- 8,50 € | |||
- 9,50 € | |||
{ | {2 von 5 Schüler:innen haben die Hausaufgaben vergessen, das sind ...Prozent.(ohne Taschenrechner).} | ||
- 10% | |||
- 20% | |||
+ 40% | |||
- 50% | |||
{75 Schüler:innen gehen in die 10. Klassen. 60% davon geben "Mathe" als Lieblingsfach an. Wie viele Schüler:innen sind das?} | |||
- 40 | |||
+ 45 | |||
- 50 | |||
- 55 | |||
{ | {Ein Sportgeschäft möchte für eine Rabattaktion die Preise mithilfe einer Tabellenkalkulation berechnen. Mit welchen Formeln lässt sich der Wert in Zelle D4 berechnen? | ||
[[Datei:Tabellenkalkulation Prozentrechnung ZP10 Test.png|rahmenlos|400x400px]]} | |||
- =B4*(1+B1/100) | |||
+ =B4-C4 | |||
+ =B4*(1-B1/100) | |||
- =B4+C4 | |||
{ Frau Schmitt verdient 2854,35€ und erhält eine Gehaltserhöhung von 2,6%. Wie viel verdient sie nach der Erhöhung?} | |||
+ 2928,56 € | |||
- 74,21 € | |||
- 2780,14 € | |||
{ Wie hoch sind die Zinsen für ein Darlehen von 6000€ für 6 Monate bei einem Zinssatz von 11,5%?} | |||
- 414,40 € | |||
- 3450 € | |||
+ 345 € | |||
{ Du erhältst zur Geburt ein Konto mit 1000€ Startkapital. Der Zinssatz der Bank bleibt bis zu deinem 18. Geburtstag gleich bei p% = 2,5%. Wie hoch ist der Kontostand dann an deinem 18. Geburtstag?} | |||
+ 1559,66 € | |||
- 559,66 € | |||
- 450 € | |||
- 1450 € | |||
</quiz> | |||
{{Box|Auswertung des Eingangstests|Schau, welche Aufgaben du schon gut lösen konntest und bei welchen du noch Schwierigkeiten hattest. Übe dann passend. | |||
* Zuordnungen Nr. 1,2 | |||
* Proportionale und antiproportionale (umgekehrt proportionale) Zuordnungen 3-8 | |||
* Prozentrechnung Nr. 9-11 | |||
* Zinsrechnung Nr. 12,13,14 (Zinseszins)|Lösung}} | |||
{{Box|Übung|Löse die Aufgaben aus dem Buch, vergleiche deine Lösungen. Nutze zur Erinnerung die Informationen in diesem Lernpfad. | |||
* Zuordnungen: S.144, Nr.1-8 | |||
* Proportionale Zuordnungen und Dreisatz: S. 143 | |||
* Umgekehrt proportionale Zuordnungen und Dreisatz: S. 144 | |||
* Prozentrechnung: S. 145 | |||
* Zinsrechnung: S. 146 ganz; S. 120, P20-P21|Üben}} | |||
{{#ev:youtube| | ===Zuordnungen=== | ||
{|class=wikitable | |||
|- | |||
!Merksatz | |||
|{{Box|Zuordnungen|Zuordnungen kommen in vielen Alltagssituationen vor. Sie können mit Worten, als Wertetabelle, als Diagramm und als Schaubild dargestellt werden.|Merksatz}} | |||
|- | |||
!Video | |||
|{{#ev:youtube|Py5J_v1b0_Q|800|left}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=pgmy707u520|width=85%|height=600px}} | |||
{{LearningApp|app=pnx04cghn01|width=85%|heiht=600px}} | |||
|} | |||
Du hast in Klasse 7 proportionale und umgekehrt proportionale (antiproportionale) Zuordnungen kennengelernt. | |||
{{#ev:youtube| | ====Proportionale Zuordnungen und Dreisatz==== | ||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
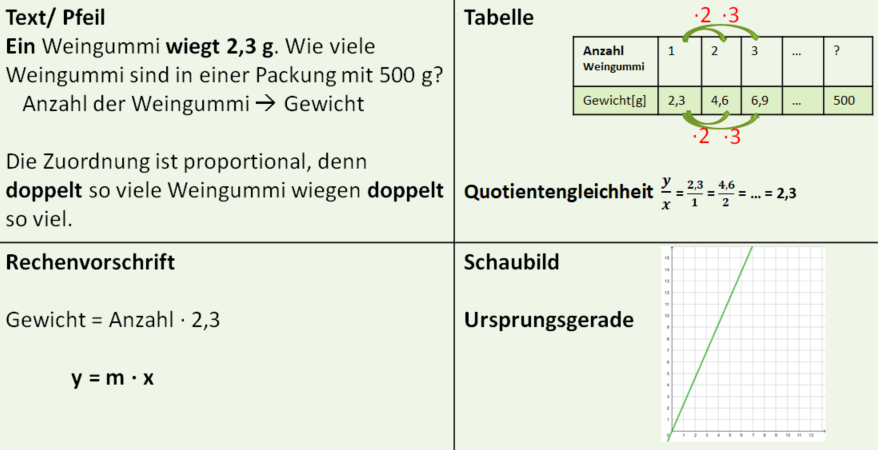
|{{Box|1=Eigenschaften proportionaler Zuordnungen|2=Eine proportionale Zuordnung liegt vor, wenn zum '''Doppelten''' (Dreifachen,…) der Eingabegröße das '''Doppelte''' (Dreifache…) der Ausgabegröße gehört. | |||
Für jedes Wertepaar in der '''Wertetabelle''' gilt '''Quotientengleichheit''':<br> | |||
<math>\tfrac{y}{x}</math> = y : x = 2,3 : 1= 4,6 : 2 = 6,9 : 3 = … = 2,3 (Jedes Weingummi ist gleich schwer und wiegt 2,3 g).<br> | |||
Für das '''Schaubild''' gilt: Alle Punkte einer proportionalen Zuordnung liegen auf einer '''Geraden durch den Ursprung''', also durch den Punkt (0I0). | |||
<br> | |||
Die '''Rechenvorschrift''' lautet: Gewicht = 2,3·Anzahl der Weingummi.|3=Merksatz}} | |||
<br> | |||
[[Datei:Proportionale_Zuordnung_Darstellungen_(Weingummi).png|rahmenlos|884x884px]] | |||
{{Box|Dreisatz bei proportionalen Zuordnungen|Bei einer proportionalen Zuordnung kann die gesuchte Größe mit dem '''Dreisatz''' (3 Schritte) berechnet werden. | |||
[[Datei:Dreisatz p schrittweises Vorgehen kurz neu.png|rahmenlos|600x600px]]|Merksatz}} | |||
|- | |||
!Videos | |||
|{{#ev:youtube|MT3hVo_BfT0|800|left}} | |||
{{#ev:youtube|M6--2jhtrKM|800|left}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=pekt1gix322|width=85%|height=400px}} | |||
Buch, S. 143, Nr. 1-7 (Vergleiche deine Lösungen mit denen hinten im Buch) | |||
|} | |||
{{Box| | ====Umgekehrt proportionale (antiproportionale) Zuordnungen==== | ||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
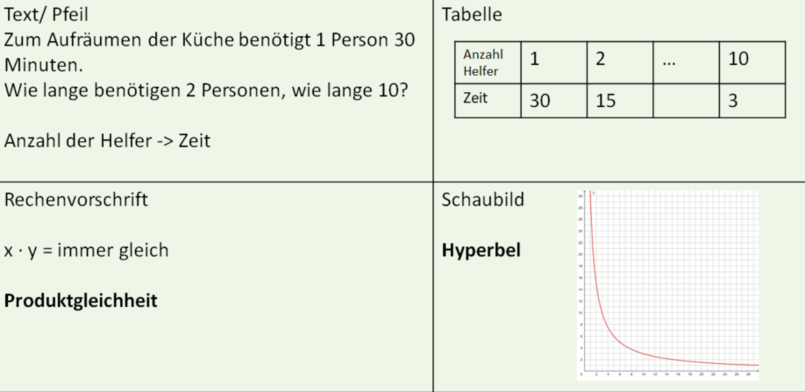
|{{Box|1=Eigenschaften umgekehrt proportionaler Zuordnungen (antiproportional)|2=Eine umgekehrt proportionale Zuordnung liegt vor, wenn zum '''Doppelten''' (Dreifachen,…) der Eingabegröße die '''Hälfte''' (Drittel...) der Ausgabegröße gehört.<br> | |||
Für jedes Wertepaar in der '''Wertetabelle''' gilt '''Produktgleichheit''':<br> | |||
y·x = 1·30 = 2·15 = 3·10 = … = 30 (Minuten).<br> | |||
Für das '''Schaubild''' gilt: Alle Punkte einer umgekehrt proportionalen Zuordnung liegen auf einer Kurve, die '''Hyperbel''', heißt. | |||
<br> | |||
Die '''Rechenvorschrift''' lautet Zeit = 30 : Anzahl der Helfer, also y = 30 : x|3=Merksatz}} | |||
<br> | |||
{{Box|Dreisatz bei umgekehrt proportionalen Zuordnungen|Bei einer umgekehrt proportionalen Zuordnung kann die gesuchte Größe mit dem '''Dreisatz''' (3 Schritte) berechnet werden.<br> [[Datei:Dreisatz up schrittweises Vorgehen kurz.png|rahmenlos|663x663px]]|Arbeitsmethode}} | |||
[[Datei:Umgekehrt proportionale Zuordnung Darstellungsmöglichkeiten.png|rahmenlos|805x805px]] | |||
|- | |||
!Videos | |||
|{{#ev:youtube|cx6MYk5wJVo|800|left|||start=0&end=273}} | |||
{{#ev:youtube|izN8-f70q2s|800|left}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=pys6bqrqj22|width=85%|height=500px}} | |||
Buch, S. 144, Nr. 1-8 (Vergleiche deine Lösungen mit denen hinten im Buch) | |||
|} | |||
===Prozentrechnung=== | ===Prozentrechnung=== | ||
====Bruch - Dezimalbruch - Prozent==== | ====Bruch - Dezimalbruch - Prozent==== | ||
{{Box|1=Prozentschreibweise|2='''Prozente''' sind Anteile mit dem Nenner '''100'''.<br> | {|class=wikitable | ||
|- | |||
!Merksätze | |||
|{{Box|1=Prozentschreibweise|2='''Prozente''' sind Anteile mit dem Nenner '''100'''.<br> | |||
1% = <math>\tfrac{1}{100}</math><br> | 1% = <math>\tfrac{1}{100}</math><br> | ||
p% = <math>\tfrac{p}{100}</math><br> | p% = <math>\tfrac{p}{100}</math><br> | ||
p heißt '''Prozentzahl''' und p'''%''' heißt '''Prozentsatz'''.|3=Arbeitsmethode}} | p heißt '''Prozentzahl''' und p'''%''' heißt '''Prozentsatz'''.|3=Arbeitsmethode}} | ||
|- | |||
!Videos | |||
|{{#ev:youtube|FbSG_MwL760|800}} | |||
{{#ev:youtube|kMbMphpQKsk|800}} | |||
{{#ev:youtube|bbjTr0YsFOs|800}} | |||
|- | |||
{{LearningApp|app=p7pk1zxdc23|width= | !Übungen | ||
|{{LearningApp|app=p7pk1zxdc23|width=85%|heigth=400px}} | |||
|} | |||
====Diagramme mit Prozentangaben==== | ====Diagramme mit Prozentangaben==== | ||
{{Box|Diagramme mit Prozentangaben|Prozentangaben werden in einen Streifendiagramm oder in einem Kreisdiagamm dargestellt.|Merksatz}} | {|class=wikitable | ||
|- | |||
!Merksätze | |||
{{#ev:youtube|0r55TGcVOyw| | |{{Box|Diagramme mit Prozentangaben|Prozentangaben werden in einen Streifendiagramm oder in einem Kreisdiagamm dargestellt.|Merksatz}} | ||
|- | |||
{{#ev:youtube|uhIhG8uHS00| | !Videos | ||
|Prozentstreifen<br> | |||
{{#ev:youtube|0r55TGcVOyw|800}} | |||
Prozentkreis<br> | |||
{{#ev:youtube|uhIhG8uHS00|800}} | |||
|} | |||
====Grundbegriffe der Prozentrechnung==== | ====Grundbegriffe der Prozentrechnung==== | ||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
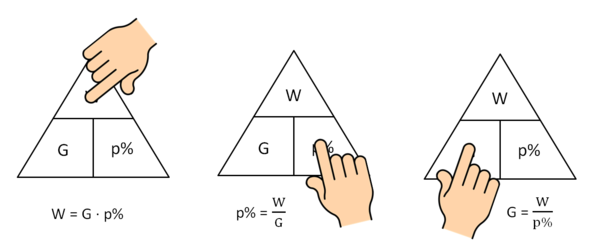
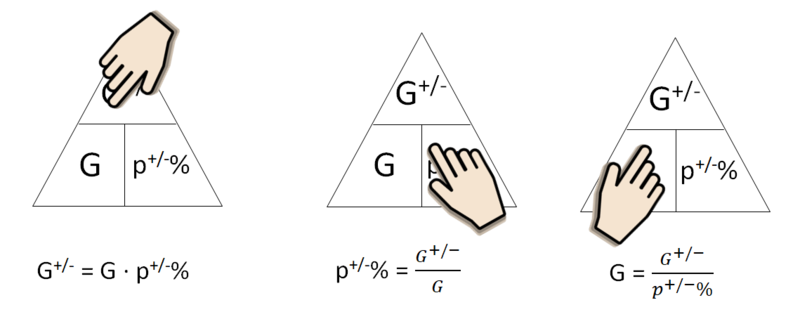
|{{Box|Grundbegriffe der Prozentrechnung|Grundwert G, Prozentwert W und Prozentsatz p%|Merksatz}}'''Grundformel der Prozentrechnung'''<br> | |||
[[Datei:Formeldreiecke Prozentrechnung mit Hand.png|600x600px]] | |||
|- | |||
!Video | |||
|{{#ev:youtube|kVIqRdUuv3g|800}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=piqochsu320|width=60%|height=400px}} | |||
|} | |||
====Prozentwert W berechnen==== | ====Prozentwert W berechnen==== | ||
{{LearningApp|app=pu4us6qqc20|width= | {|class=wikitable | ||
|- | |||
!Merksätze | |||
|{{Box|Prozentwert W berechnen| | |||
[[Datei:Prozentwert W berechnen Beispiel 2 Möglichkeiten berichtigt.png|600x600px]]|Merksatz}}<br> | |||
|- | |||
!Videos | |||
|{{#ev:youtube|u0ofHvw7JNo|800}} | |||
{{#ev:youtube|8rQ6tpEIiHk|800}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=pu4us6qqc20|width=85%|height=800px}} | |||
{{h5p-zum|id=20374|height=232}} | {{h5p-zum|id=20374|height=232}} | ||
|} | |||
====Prozentsatz p% berechnen==== | ====Prozentsatz p% berechnen==== | ||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
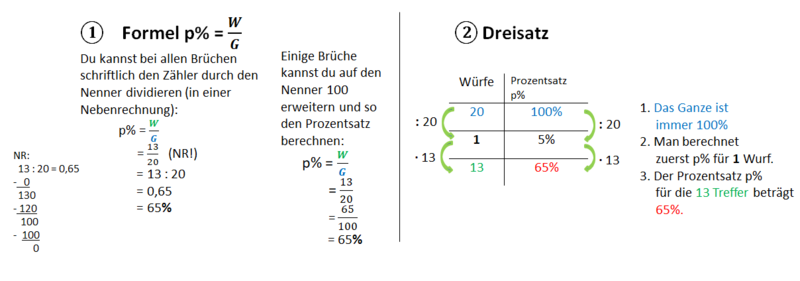
|{{Box|Prozentsatz p% berechnen| | |||
[[Datei:Prozentsatz berechnen 2 Möglichkeiten berichtigt.png|800x600px]]|Merksatz}}<br> | |||
|- | |||
!Videos | |||
|{{#ev:youtube|1Mn6kbjqcb8|800}} | |||
{{#ev:youtube|YdBcJa8-81s|800}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=pd83efk6t20|width=85%|height=900px}} | |||
|} | |||
====Grundwert G berechnen==== | ====Grundwert G berechnen==== | ||
{{h5p-zum|id=20374|height=232}} | {|class=wikitable | ||
{{LearningApp|app=11309986|width= | |- | ||
!Merksätze | |||
|{{Box|Grundwert G berechnen| | |||
[[Datei:Grundwert G berechnen 2 Möglichkeiten Bild berichtigt.png|800x800px]]|Merksatz}}<br> | |||
|- | |||
!Videos | |||
|{{#ev:youtube|rs7dsg_t3H4|800}} | |||
{{#ev:youtube|rATJxqaoyYU|800}} | |||
{{#ev:youtube|gtEAmp8-K-8|800}} | |||
|- | |||
!Übungen | |||
|{{h5p-zum|id=20374|height=232}} | |||
{{LearningApp|app=11309986|width=85%|height=500px}} | |||
|} | |||
====Vermehrter und verminderter Grundwert==== | ====Vermehrter und verminderter Grundwert==== | ||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
|[[Datei:Formeldreieck vermehrter Grundwert mit Hand.png|rahmenlos|center|800x800px]] | |||
|- | |||
!Videos | |||
|{{#ev:youtube|gq0clIHMgiY|800}} | |||
{{#ev:youtube|RAKS6Iad9lQ|800}} | |||
{{#ev:youtube|vQAjV3g8Frw|800}} | |||
|- | |||
!Übungen | |||
|{{h5p-zum|id=10428|height=200px}} | |||
{{LearningApp|app=pmm3dug7324|width=85%|height=400px}} | |||
Buch, s. 145, Nr. 1-6 (Vergleiche deine Lösungen mit denen hinten im Buch.) | |||
|} | |||
===Zinsrechnung=== | ===Zinsrechnung=== | ||
{|class=wikitable | |||
{{ | |- | ||
{{ | !Merksätze | ||
{{LearningApp|app= | | | ||
|- | |||
!Videos | |||
|{{#ev:youtube|5cOBrbaX4-Y|800}} | |||
{{#ev:youtube|JdRYVqql5f4|800}} | |||
|- | |||
!Übungen | |||
|{{LearningApp|app=p5sp292za25|width=85%|height=400px}} | |||
Buch, S. 146, Nr. 1-4 (Vergleiche deine Lösungen mit denen hinten im Buch.) | |||
|} | |||
Aktuelle Version vom 11. März 2025, 13:25 Uhr
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag
Zuordnungen, Prozent-und Zinsrechnung
Einstiegstest: Zuordnungen, Prozent- und Zinsrechnung (hilfsmittelfreier Teil)
Zuordnungen
| Merksatz | |
|---|---|
| Video | |
| Übungen |
|
Du hast in Klasse 7 proportionale und umgekehrt proportionale (antiproportionale) Zuordnungen kennengelernt.
Proportionale Zuordnungen und Dreisatz
| Merksätze | |
|---|---|
| Videos | |
| Übungen |
Buch, S. 143, Nr. 1-7 (Vergleiche deine Lösungen mit denen hinten im Buch) |
Umgekehrt proportionale (antiproportionale) Zuordnungen
| Merksätze |
|
|---|---|
| Videos | |
| Übungen |
Buch, S. 144, Nr. 1-8 (Vergleiche deine Lösungen mit denen hinten im Buch) |
Prozentrechnung
Bruch - Dezimalbruch - Prozent
| Merksätze | |
|---|---|
| Videos | |
| Übungen |
|
Diagramme mit Prozentangaben
| Merksätze | |
|---|---|
| Videos | Prozentstreifen Prozentkreis |
Grundbegriffe der Prozentrechnung
| Merksätze |
Grundformel der Prozentrechnung |
|---|---|
| Video | |
| Übungen |
|
Prozentwert W berechnen
| Merksätze |
|
|---|---|
| Videos | |
| Übungen |
|
Prozentsatz p% berechnen
| Merksätze |
|
|---|---|
| Videos | |
| Übungen |
|
Grundwert G berechnen
| Merksätze |
|
|---|---|
| Videos | |
| Übungen |
|
Vermehrter und verminderter Grundwert
| Merksätze | |
|---|---|
| Videos | |
| Übungen |
Buch, s. 145, Nr. 1-6 (Vergleiche deine Lösungen mit denen hinten im Buch.) |
Zinsrechnung
| Merksätze | |
|---|---|
| Videos | |
| Übungen |
Buch, S. 146, Nr. 1-4 (Vergleiche deine Lösungen mit denen hinten im Buch.) |