Benutzer:Buss-Haskert/Pythagoras/Satz des Pythagoras

zurück zur Seite der Herta-Lebenstein-Realschule

Satz des Pythagoras - Startseite

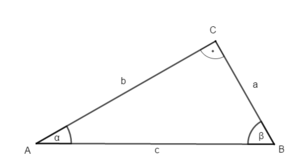
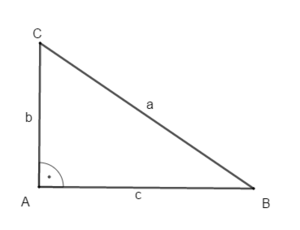
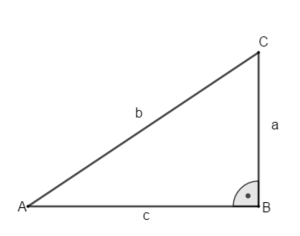
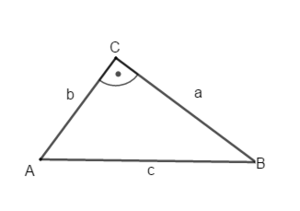
1) Rechtwinklige Dreiecke (Konstruktion und Bezeichnungen)
2) Satz des Pythagoras
3) Anwendungen
   3.1) Anwendungen in geometrischen Figuren
   3.2) Anwendungen im Raum
   3.3) Anwendungen in Sachsituationen

   3.4 Anwendungen im Koordinatensystem

2 Satz des Pythagoras

GeoGebra-Buch des FLINK-Teams https://www.geogebra.org/m/jnaxjfbr

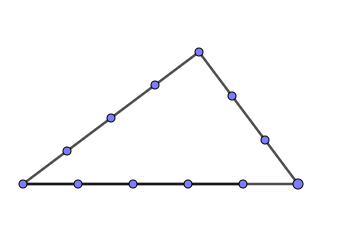
2.1 12-Knoten-Seil

12-Knoten-Seil

Schon im alten Ägypten (lange vor Pythagoras), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten.
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. Spanne nun das Seil so, dass du 5 Teile unten (Hypotenuse) und jeweils 3 bzw. 4 Teile an den Seiten (Katheten) hast.
Was beobachtest du?

Prüfe deine Beobachtung mithilfe des nachfolgenden Applets.
Originallink https://www.geogebra.org/m/xaAVwK4T

Applet von Pöchtrager

Originallink https://www.geogebra.org/m/jcbcvfxd

Was hat das mit dem Satz des Pythagoras zu tun?

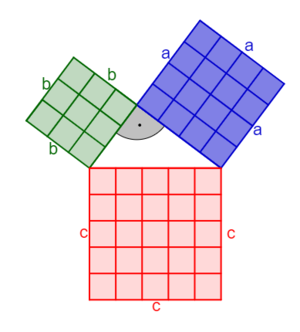
2.2 Satz des Pythagoras - Herleitung

Originallink https://www.geogebra.org/m/AgezqDax

Applet von Pöchtrager
Prüfe, ob diese Aussage in jedem Dreieck gilt:
Originallink https://www.geogebra.org/m/vs8heusr

Applet von Elschenbroich

2.3 Der Satz des Pythagoras

Hefteintrag: Satz des Pythagoras

In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse genauso groß wie die Summe der Quadrate über den Katheten.
Für ein rechtwinkliges Dreieck mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras

a² + b² = c².

2.4 Beweise zum Satz des Pythagoras

Überprüfe die Aussage des Satzes von Pythagoras mithilfe des nachfolgenden Applets.
Originallink https://www.geogebra.org/m/j3UksqZs

Applet von Pöchtrager

Zerlegungsbeweise

Es gibt viele Möglichkeiten, den Satz des Pythagoras zu beweisen. Die nachfolgenden GeoGebra-Applets nutzen die Zerlegungsmethode, d.h. die Quadrate über den Katheten werden so zerlegt, dass sie neu zusammengelegt das Hypotenusenquadrat ergeben. Erkläre jeweils!

Zerlegungsbeweis nach Perigal:
Originallink https://www.geogebra.org/m/sfa9y6er

Beweis Nr. 2:
Originallink https://www.geogebra.org/m/EdufUSRu

Applet von J. Mil

Beweis Nr. 3:
Originallink https://www.geogebra.org/m/E5sNk6Z8

Applet von B.Lachner

Beweis Nr. 4:
Originallink https://www.geogebra.org/m/ND4QUNXn

Applet von Pöchtrager

Beweis Nr. 5:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Auch im Lied von Dorfuchs findest du einen Beweis für den Satz des Pythagoras:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

2.5 Erste Übungen

Übung 1- Begriffe zuordnen

Ordne in der nachfolgenden LearningApp die Begriffe Kathete, Hypotenuse, Kathetenquadrat und Hypotenusenquadrat passend zu. Bearbeite dann die GeoGebra-Applets des FLINK-Teams darunter.

Originallink https://www.geogebra.org/m/exvvm2mw

Originallink https://www.geogebra.org/m/anu6ybxh

Applets des FLINK-Teams

Übung 2 - Grundlagen online

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 1
• 2
• 3
• 4
• 5

Danach bearbeite die Übungen der LearningApp.

Übung 3 - Grundlagen Buch

Löse die Aufgaben aus dem Buch. Übertrage die Skizze in dein Heft, markiere die Hypotenuse rot und formuliere den Satz des Pythagoras. (Achte darauf, dass deine Skizze ein rechtwinkliges Dreieck ist.)

• S. 111 Nr. 2
• S. 111 Nr. 3

In Nr. 3 gibt es jeweils 3 rechtwinklige Dreiecke pro Figur, das große gesamte Dreieck mit den Katheten x und y und der Hypotenuse (z+w) und die zwei kleinen Dreiecke mit jeweils der Seite y als Kathete.

2.6 Fehlende Seitenlängen in rechtwinkligen Dreiecken berechnen mit dem Satz des Pythagoras

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Fehlende Seitenlängen berechnen

Mithilfe des Satzes von Pythagoras lassen sich in rechtwinkligen Dreiecken fehlende Seitenlängen berechnen. Übertrage die Beispiele in dein Heft.

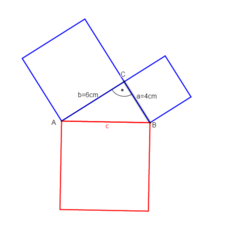
Beispiel 1: Die Katheten sind gegeben und die Hypotenuse ist gesucht.

geg: rechtwinkliges Dreieck mit γ=90°;   Katheten: a = 4cm; b = 6cm
ges: Hypotenuse c

c² = a² + b²   |$\surd$
c = $\sqrt{\text{a² + b²}}$   |Werte einsetzen
c = $\sqrt{\text{4² + 6²}}$   |berechnen
(c = $\sqrt{52}$   diesen Schritt musst du nicht notieren)
c $\approx$7,2 [cm]

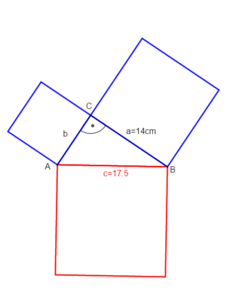
Beispiel 2: Die Hypotenuse und eine Kathete sind gegeben und die andere Kathete ist gesucht.

geg: rechtwinkliges Dreieck mit γ=90°;   Kathete: a = 14cm; Hypotenuse c = 17,5cm

ges: Kathete b

a² + b² = c²   |-a²
b² = c² - a²   |$\surd$
b = $\sqrt{\text{c² - a²}}$   |Werte einsetzen
b = $\sqrt{\text{17,5² - 14²}}$   |berechnen
(b = $\sqrt{110,25}$   diesen Schritt musst du nicht notieren)
b = 10,5 [cm]

Hinweis zum Runden: Runde auf so viele Nachkommastellen, wie die Werte in der Aufgabenstellung haben.

Übung 4 - LearningApps

Löse die nachfolgenden Learningapps und die GeoGebra-Applets des FLINK-Teams, achte auf die Schreibweise der Lösungen. Diese sollst du bei der Lösung der Aufgaben aus dem Buch beachten.

Originallink https://www.geogebra.org/m/wcp6h9f9

Originallink https://www.geogebra.org/m/gb4udcdx (5 Beispiele)

Übung 5 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13

Danach bearbeite die Aufgaben in den GeoGebra-Applets.

Übungen (GeoGebra-Applets von Pöchtrager)
Originallink https://www.geogebra.org/m/vdp56qtd

Originallink https://www.geogebra.org/m/abeswgx8

Originallink https://www.geogebra.org/m/tddbdued

Übung 6

Löse die Aufgaben aus dem Buch. Gehe dabei schrittweise vor:
1. Schritt: Prüfe, dass das Dreieck rechtwinklig ist.
2. Schritt: Entscheide, welche Seiten die Katheten und welche Seite die Hypotenuse ist.
3. Schritt: Notiere im Heft geg:... und ges:... wie in den Beispielen oben.
4. Schritt: Berechne dann wie in den Beispielen oben. Notiere vollständig und runde richtig.

• S. 111 Nr. 4
• S. 111 Nr. 5
• S. 111 Nr. 6 (mit Skizze!)
• S. 111 Nr. 7 (mit Skizze!)

In Aufgabenteil a) ist eine Kathete 4cm lang, von der anderen Kathete kennst du nur das Quadrat (20cm²). Gesucht ist die Hypotenuse x.
x² = 4² + 20   (20 ist schon das Quadrat der zweiten Kathete)
x = $\sqrt{\text{16 + 20}}$

x = 6 [cm]

In Aufgabenteil c) sind die Katheten gleich lang, das Quadrat der Hypotenuse ist gegeben.
50 = x² + x²
50 = 2x²   |:2
25 = x²

...

Um x zu berechnen, teile das Dreieck in zwei rechtwinklige Teildreiecke ein (wie in der Skizze gegeben) und berechne die einzelnen Teilstrecken x₁ und x₂. x = x₁ + x₂

Wichtig für die Skizze ist die Angabe, dass $\gamma$=90° ist.

geg: Flächeninhalt A = 24,0 cm²; a = 7,2 cm; $\gamma$ = 90°.
Problem: Die Seiten b und c sind gesucht.
Berechne b mithilfe der Flächeninhaltsformel für rechtwinklige Dreiecke: Wenn $\gamma$ = 90° ist, dann ist b die Höhe zur Seite a. Daher gilt A = $\frac{a \cdot b}{2}$ = $\frac{1}{2}$$\cdot$a$\cdot$b. Stelle diese Gleichung nach b um und berechne so die Länge von b (Lösung: b $\approx$ 6,7 cm).

Bestimme nun c mit dem Satz des Pythagoras.

Übung 7 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 15
• 16
• 17
• 18
• 19
• 20
• 21

2.7 Umkehrung des Satzes von Pythagoras

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 8: Umkehrung des Satzes von Pythagroas

Mit der Umkehrung des Satzes von Pythagoras kannst du prüfen, ob ein Dreieck rechtwinklig ist:
Prüfe, ob die Summe der Quadrate der kürzeren Seiten genauso groß sind wie das Quadrat der längsten Seite.
Prüfe also, ob a² + b² = c² gilt (mit a und b kürzere Seiten, c längste Seite).
Wenn du eine wahre Aussage erhältst, ist das Dreieck rechtwinklig.

• S. 111 Nr. 8
• Nr. 14 auf der Seite Aufgabenfuchs

a) a und b sind die kürzeren Seiten, c ist die längste Seite.
a² + b² = c²
8² + 15² = 17²
289 = 289 (w)

Also ist das Dreieck rechtwinklig.

Übung 9 - Umkehrung des Satzes von Pythagoras (online)

Bearbeite das nachfolgende GeoGebra-Applet des FLINK-Teams.

Originallink https://www.geogebra.org/m/qf4ggwcx

Originallink https://www.geogebra.org/m/hrycjnge

Applets des FLINK-Teams

2.8 Besondere Figuren konstruieren mit dem Satz des Pythagoras

Übung 10 - Pythagorasschnecke

Konstruiere die "Pythagoras-Schnecke", wie im Buch gezeigt.

• S. 112 Nr. 9

Beschreibe dein Vorgehen mit Fachbegriffen!

GeoGebra-Applet zu Nr. 9
Originallink https://www.geogebra.org/m/jnkr8pak

Applet von C.Buß-Haskert

Konstruiere mit einer verkürzten Schnecke. Beginne bei der Schnecke, die die Katheten mit den Längen 1 und 6(=$\sqrt{36}$)hat. Die Hypotenuse dieses rechtwinkligen Dreiecks hat die Länge $\sqrt{37}$. Ergänze noch ein weiteres rechtwinkliges Dreieck.

Mögliche Konstruktionsbeschreibung:
Die Hypotenuse des gegebenen Dreiecks ist die Kathete des neuen Dreiecks. An ihr äußeres Ende zeichne ich in einem rechten Winkel die Kathete mit der Länge 1cm. Die Hypotenuse des neuen Dreiecks hat dann die Länge $\sqrt{38}$.
Denn:
$\sqrt{37}$² + 1² = x²
37 + 1 = x²
38 = x²   |$\sqrt{...}$

$\sqrt{38}$ = x.

Eine weitere besondere Figur, die mit dem Satz des Pythagoras konstruiert wird, ist der Pythagoras-Baum. Die Konstruktion zeigt das nachfolgende Applet.
Originallink https://www.geogebra.org/m/pj9y28s5

(Appelt von Pöchtrager)

Übung 11: Pythagoreische Zahlen

Rechtwinklige Dreiecke mit natürlichen Zahlen als Seitenlängen heißen pythagoreische Zahlen. Ein Beispiel hast du beim 12-Knoten-Seil kennengelernt.
Hier gilt: 3² + 4² = 5² (alle Zahlen sind natürlichen Zahlen).
Löse Buch

• S. 112 Nr. 11

a) (9;12;15) Die beiden kürzeren Seiten sind ggf. die Katheten, die längere Seite ist die Hypotenuse. Prüfe also:
9² + 12² = 15²
81 + 144 = 225
225 = 225 (w)
Die Aussage ist wahr, daher sind die Zahlen (9;12;15) also pythagoreische Zahlen.
Ergibt sich eine falsche Aussage, so sind die Zahlen keine pythagoreischen Zahlen.

Prüfe die übrigen Beispiele ebenso.

Vervielfache (3;4;5) und prüfe wie in Teil a).

Verdoppelt: (6;8;10)

Berechne mit dem Satz des Pythagoras die fehlende Seitenlänge. Das Ergebnis muss jeweils eine natürliche Zahl sein.

3) Anwendungen