Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen Teil2: Unterschied zwischen den Versionen
(Unterseite angelegt) Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (16 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
{{Fortsetzung|vorher=zurück zur Übersicht Vorbereitungskurs ZP 10|vorherlink=Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik}}<br> | |||
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag | |||
{{Navigation verstecken|[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Größen| 1. Zahlen und Größen]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Zuordnungen|2. Zuordnungen und Prozent-und Zinsrechnung]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Gleichungen|3. Terme und Gleichungen (lineare Gleichungen, lineare Gleichungssysteme (LGS) und quadratische Gleichungen)]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen|4. Funktionen: Lineare Funktionen]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen Teil2|5. Funktionen: Quadratische Funktionen]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie|6. Geometrie: Winkel in Figuren; Flächen- und Körperberechnungen; Pythagoras, Strahlensätze, Trigonometrie]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik|7. Diagramme, Statistik]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit|8. Wahrscheinlichkeitsrechnung]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Exponentiafunktion|9. Wachstum und Exponentialfunktion]] | |||
}} | |||
==Funktionen: Quadratische Funktionen== | ==Funktionen: Quadratische Funktionen== | ||
===Einstiegstest: '''<big>Quadratische Funktionen</big>''' (hilfsmittelfreier Teil)=== | ===Einstiegstest: '''<big>Quadratische Funktionen</big>''' (hilfsmittelfreier Teil)=== | ||
| Zeile 42: | Zeile 58: | ||
- f(x) = 3(x+4)² + 2 | - f(x) = 3(x+4)² + 2 | ||
- f(x) = (x - 4)² + 3 | - f(x) = (x - 4)² + 3 | ||
{ Wandle die Funktionsgleichung von f(x) = (x + 2)² - 3 in die Normalform um. Löse im Heft.} | |||
+ x² + 4x + 1 | |||
- x² + 4x - 3 | |||
- x² + 2x - 3 | |||
- x² + 2x + 1 | |||
{ Wandle die Funktionsgleichung von f(x) = x² + 6x + 5 in die Scheitelpunktform um. Löse im Heft.} | |||
- (x + 6)² + 5 | |||
- (x - 6)² - 5 | |||
+ (x + 3)² - 4 | |||
- (x + 3)² + 4 | |||
{ Wie viele Nullstellen kann eine quadratische Funktion haben?} | { Wie viele Nullstellen kann eine quadratische Funktion haben?} | ||
| Zeile 56: | Zeile 84: | ||
{ Bestimme die Nullstellen der Funktion f(x) = x² - 10x + 16. Berechne im Heft.} | { Bestimme die Nullstellen der Funktion f(x) = x² - 10x + 16. Berechne im Heft.} | ||
+ N(0|2) | + N(2|0) | ||
- N(0|- | - N(-10|0) | ||
- N(0| | - N(16|0) | ||
+ N(0| | + N(8|0) | ||
{ Eine Parabel hat den Scheitelpunkt S(0|-3) und geht durch den Punkt P(2|-2). Bestimme die Funktionsgleichung. Löse im Heft.} | |||
+ f(x) = <math>\tfrac{1}{4}</math>x² - 3 | |||
- f(x) = 2x² - 3 | |||
- f(x) = -2x² - 3 | |||
- f(x) = 2x² - 2x + 3 | |||
</quiz> | |||
{{Box|Auswertung des Eingangstests|Schau, welche Aufgaben du schon gut lösen konntest und bei welchen du noch Schwierigkeiten hattest. Übe dann passend. | |||
* Scheitelpunktform Nr. 1-6 | |||
* Scheitelpunktform und Normalform Nr. 7,8 | |||
* Nullstellen bestimmen Nr. 9-11 | |||
* Funktionsgleichung aufstellen Nr. 12|Lösung}} | |||
{{Box|Übung|Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen mit denen hinten im Buch. | |||
* S. 123, P12 - P16 | |||
* AB Quadratische Funktionen - Anwendungsaufgaben|Üben}} | |||
===Quadratische Funktionen=== | |||
{{Box|1=Quadratische Funktionen|2=Es gibt verschiedene Formen quadratischer Funktionen. | |||
* Normalform: f(x) = x² | |||
* Scheitelpunktform: f(x) = a(x + d)² + e mit S(-d|e) | |||
* allgemeine Form: f(x) = ax² + bx + c | |||
|3=Merksatz}} | |||
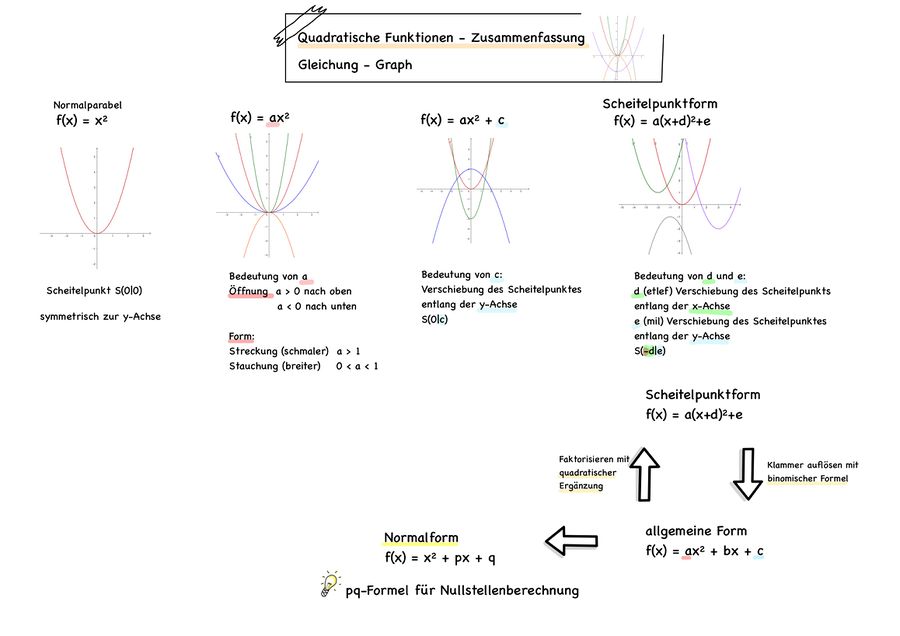
Zusammenfassungen:<br> | |||
[[Datei:Quadratische Funktionen Zusammenfassung S.1.jpg|rahmenlos|900x900px]] | |||
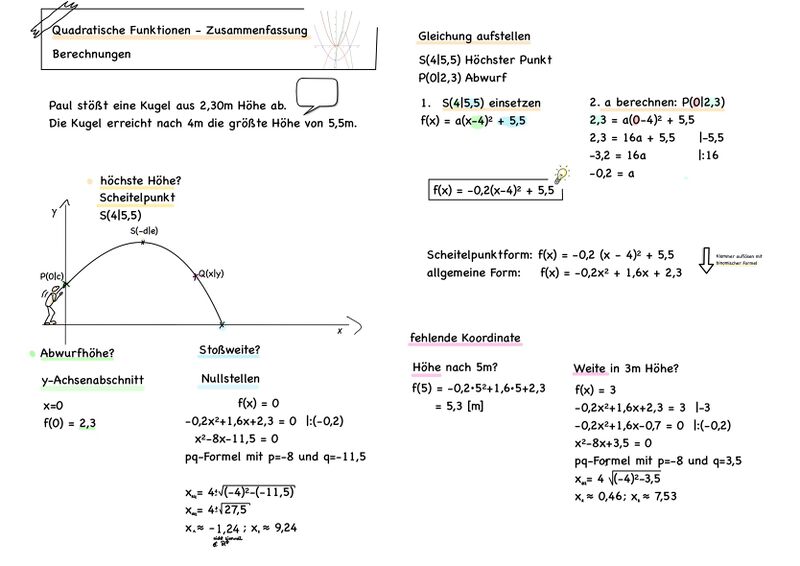
<br> | |||
[[Datei:Zusammenfassung quadratische Funktionen 2 neu.jpg|rahmenlos|800x800px]] | |||
====Die Scheitelpunktform quadratischer Funktionen==== | |||
{{Box|1=Scheitelpunktform|2=Die Scheitelpunktform quadratischer Funktionen lautet f(x) = a(x + d)² + e. Wir haben die Bedeutung der Parameter a(nton), d(etlef) und e(mil) erarbeitet. Wende dein Wissen in den nachfolgenden Übungen an.|3=Üben}} | |||
{{LearningApp|app=pq6e32wtk20|width=100%|height=400px}} | |||
{{LearningApp|app=2767802|width=100%|height=600px}} | |||
====Quadratische Funktionen: Scheitelpunktform und Normalform==== | |||
Du kannst die Formen der Quadratischen Funktionen umwandeln: | |||
<div class="grid"> | |||
<div class="width-1-2">Von der Scheitelpunktform zur Normalform | |||
{{#ev:youtube|TqLEqrbmRcU|420|center}} | |||
Beispiel:<br> | |||
f(x) = (x + 3)² - 4 |1. binomische Formel<br> | |||
= x² + 2·x·3 + 3² - 4<br> | |||
= x² + 6x + 9 - 4<br> | |||
= x² + 6x + 5<br> | |||
Die Normalform eignet sich gut zur Nullstellenberechnung, denn hier kannst du die p-q-Formel anwenden. | |||
</div> | |||
<div class="width-1-2">Von der Normalform zur Scheitelpunktform | |||
{{#ev:youtube|ZS3ktdMePpQ|420|center}} | |||
Beispiel:<br> | |||
f(x) = x² + 8x - 4 |quadratische Ergänzung <math>\left ( \frac{8}{2} \right )^2</math>= 4² = 16<br> | |||
= x² + 8x + 16 - 16 - 4 |1. binomische Formel<br> | |||
= (x + 4)² - 16 - 4 <br> | |||
= (x + 4)² - 20<br> | |||
Also lautet der Scheitelpunkt S(-4|-20)<br> | |||
Möchtest du anhand der Funktionsgleichung den Scheitelpunkt ablesen, wandle diese also in die Scheitelpunktform um.</div> | |||
</div> | |||
====Quadratische Funktionen: Nullstellen bestimmen==== | |||
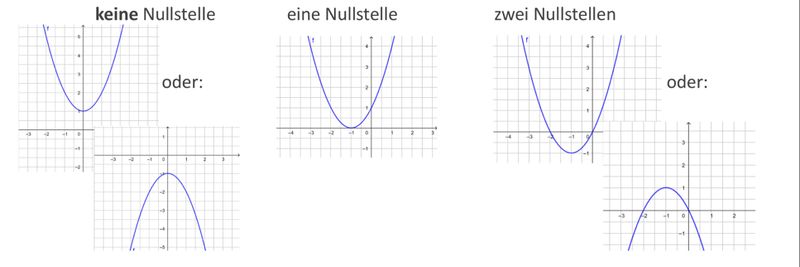
Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen. <br> Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen:<br> | |||
[[Datei:Anzahl der Nullstellen .jpg|rahmenlos|800x800px]]<br> | |||
{{Box|Übung: Anzahl der Nullstellen|Wie viele Nullstellen hat die Parabel jeweils? Ordne in der LearningApp und im Quiz passend zu. | |||
|Üben}} | |||
{{LearningApp|app=p8s7yei1v21|width=100%|height=400px}} | |||
{{LearningApp|app=pvhfbdc0v22|width=100%|height=400px}} | |||
Tipp: Bestimme zunächst die Lage des Scheitelpunktes und die Öffnungsrichtung der Parabel. Ordne dann passend zu: | |||
<div class="zuordnungs-quiz"> | |||
{| | |||
|keine||f(x) = x² + 3||f(x) = -2x² - 5||f(x) = (x+2)² + 1 | |||
|- | |||
|eine||f(x) = x²||f(x) = (x - 4)²||f(x) = -(x+2)² | |||
|- | |||
|zwei||f(x) = x² - 3||f(x) = -2x² + 5||f(x) = (x+2)² - 1 | |||
|} | |||
</div> | |||
{{Box|1=Nullstellen quadratischer Funktionen berechnen|2=Die Nullstellen sind die Schnittpunkte der Parabel mit der x-Achse, also gilt immer '''f(x) = 0'''. | |||
Du erhältst also immer eine quadratische Gleichung (rein quadratisch oder gemischt quadratisch). Wie du diese löst, hast du im 1. Themenblock erarbeitet, es sind zur Wiederholung jeweils Beispiele notiert.|3=Merksatz}} | |||
<u><big>1. Form: f(x) = ax² </big></u><br> | |||
Beispiel: f(x) = 3x²<br> | |||
f(x) = 0<br> | |||
3x² = 0 |:3<br> | |||
x² = 0 |<math>\surd</math><br> | |||
x = 0 <br> | |||
N(0|0)<br> | |||
Natürlich hat jede Parabel mit der Funktionsgleichung f(x) = ax² die Nullstelle N(0|0), denn ihr Scheitelpunkt liegt im Ursprung. Der Scheitelpunkt ist also die Nullstelle. | |||
<u><big>2. Form: f(x) = ax² + c </big></u> | |||
Beispiel: f(x) = 0,5x² - 8<br> | |||
f(x) = 0<br> | |||
0,5x² - 8 = 0 |+8<br> | |||
0,5x² = 8 |:0,5<br> | |||
x² = 16 |<math>\surd</math><br> | |||
x<sub>1</sub> = - <math>\sqrt{16}</math> und x<sub>2</sub> = + <math>\sqrt{16}</math><br> | |||
x<sub>1</sub> = -4 und x<sub>2</sub> = +4 | |||
<br> | |||
N<sub>1</sub>(-4|0) und N<sub>2</sub>(4|0)<br> | |||
<u><big>3. Form: Scheitelpunktform f(x) = a(x+d)²+e </big></u> | |||
Beispiel: f(x) = 2(x + 2)² - 18<br> | |||
f(x) = 0<br> | |||
2(x + 2)² - 18 = 0 |+18<br> | |||
2(x + 2)² = 18 |:2<br> | |||
(x + 2)² = 9 |<math>\surd</math><br> | |||
x<sub>1</sub> + 2 = - <math>\sqrt{9}</math> und x<sub>2</sub> + 2 = + <math>\sqrt{9}</math><br> | |||
x<sub>1</sub> + 2 = -3 und x<sub>2</sub> + 2 = 3 |-2<br> | |||
x<sub>1</sub> = - 3 - 2 und x<sub>2</sub> = + 3 - 2 <br> | |||
x<sub>1</sub> = -5 und x<sub>2</sub> = 1 <br> | |||
N<sub>1</sub>(-5|0) und N<sub>2</sub>(1|0)<br> | |||
Der Scheitelpunkt der Parabel liegt immer in der Mitte zwischen den beiden Nullstellen. Die x-Koordinate des Scheitelpunktes muss also -2 heißen. (x-Koordinate zwischen x = -5 und x = 1).<br> | |||
Dies passt zum Scheitelpunkt S(-2|-18), der aus der Parabelgleichung abgelesen werden kann. | |||
<u><big>4. Form: Normalform f(x) = x² + px + q </big></u><br> | |||
Lösung mit der p-q-Formel:<br> | |||
Normalform: f(x) = x² + px + q<br> | |||
x² + px + q = 0<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{p}{2} \pm \sqrt{\left ( \frac{p}{2} \right )^2-q}</math><br> | |||
Beispiel: f(x) = x² -6x + 5<br> | |||
f(x) = 0<br> | |||
x² - 6x + 5 = 0 | pq-Formel mit p=-6 und q=5<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{-6}{2} \pm \sqrt{\left ( \frac{-6}{2} \right )^2-5}</math><br> | |||
x<sub>1/2</sub> = 3 <math> \pm \sqrt{9-5}</math><br> | |||
x<sub>1/2</sub> = 3 <math>\pm \sqrt{4}</math><br> | |||
x<sub>1/2</sub> = 3<math> \pm </math>2<br> | |||
x<sub>1</sub> = 3 - 2 = 1 ; x<sub>2</sub> = 3+2 = 5 | |||
N<sub>1</sub>(1|0) und N<sub>2</sub>(5|0)<br> | |||
{{Lösung versteckt|1=<u><big>4. Form: Normalform f(x) = x² + px + q (mit quadratischer Ergänzung )</big></u> | |||
Beispiel: f(x) = x² -6x + 5<br> | |||
f(x) = 0<br> | |||
x² - 6x + 5 = 0 | quadratische Ergänzung <math>\left ( \frac{6}{2} \right )^2 = 3^2</math><br> | |||
x² - 6x + 3² - 3² + 5 = 0 | 2. binomische Formel <br> | |||
(x - 3)² - 9 + 5 = 0 <br> | |||
(x - 3)² - 4 = 0 | nun hast du wieder die Scheitelpunktform und geht wie in Bsp 3 vor: +4<br> | |||
(x - 3)² = 4 |<math>\surd</math><br> | |||
x<sub>1</sub> - 3 = -2 und x<sub>2</sub> - 3 = 2 |+3<br> | |||
x<sub>1</sub> = -2 + 3 und x<sub>2</sub> = 2 + 3 <br> | |||
x<sub>1</sub> = 1 und x<sub>2</sub> = 5 <br> | |||
N<sub>1</sub>(1|0) und N<sub>2</sub>(5|0)<br>|2=Lösung mit quadratischer Ergänzung|3=Verbergen}} | |||
<u><big>5. Form: allgemeine Form f(x) = ax² + bx + c </big></u><br> | |||
Wandle zunächst in die Normalform um.<br> | |||
Wende dann wieder die p-q-Formel an.<br> | |||
Beispiel: f(x) = 2x² + 12x + 10<br> | |||
f(x) = 0<br> | |||
2x² + 12x + 10 = 0 |:2 (Ziel: Normalform)<br> | |||
x² + 6x + 5 = 0 | pq-Formel mit p=6 und q=5<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{6}{2} \pm \sqrt{\left ( \frac{6}{2} \right )^2-5}</math><br> | |||
x<sub>1/2</sub> = -3 <math> \pm \sqrt{9-5}</math><br> | |||
x<sub>1/2</sub> = -3 <math>\pm \sqrt{4}</math><br> | |||
x<sub>1/2</sub> = -3<math> \pm </math>2<br> | |||
x<sub>1</sub> = -3 - 2 = -5 ; x<sub>2</sub> = -3+2 = -1 | |||
N<sub>1</sub>(-5|0) und N<sub>2</sub>(-1|0)<br> | |||
====Quadratische Funktionen: Funktionsgleichung aufstellen==== | |||
{{Box|1=Funktionsgleichung einer quadratischen Funktion bestimmen|2=Um die Funktionsgleichung einer quadratischen Funktion aufzustellen, musst du wissen, wie groß a, d und e sind. Du brauchst also | |||
* den Scheitelpunkt S(-d|e) und | |||
* einen weiteren Punkt auf der Parabel, um den Streckungsfaktor a zu bestimmen. | |||
Mit den Werten kannst die dann die Funktionsgleichung in der Scheitelpunktform angeben.|3=Merksatz}} | |||
Beispiel:<br> | |||
Eine Parabel hat den Scheitelpunkt S(0|-3) und geht durch den Punkt P(2|-2).<br> | |||
f(x) = a(x + d)² + e |Setze für d=0 und e=-3 ein<br> | |||
f(x) = a(x - 0)² + (-3)<br> | |||
f(x) = ax² - 3 |Setze die Koordinaten des Punkte P ein (Punktprobe)<br> | |||
-2 = a·2² - 3 <br> | |||
-2 = 4a - 3 |+3<br> | |||
1 = 4a |:4<br> | |||
<math>\tfrac{1}{4}</math> = a<br> | |||
Also lautet die Funktionsgleichung der Parabel f(x) = <math>\tfrac{1}{4}</math>x² - 3. | |||
===Modellieren - Anwendungsaufgaben=== | |||
- | Es gibt besondere Punkte, die in Anwendungen immer wieder von Bedeutung sind: | ||
*Scheitelpunkt | |||
*Nullstellen | |||
*Schnittpunkt mit der y-Achse | |||
*Koordinaten eines beliebigen Punktes | |||
Verwende zur Lösung der Aufgabe die verschiedenen Darstellungsformen und die wiederholten Methoden zur Berechnung der verschiedenen besonderen Punkte. | |||
Aktuelle Version vom 5. November 2024, 10:30 Uhr
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag
Funktionen: Quadratische Funktionen
Einstiegstest: Quadratische Funktionen (hilfsmittelfreier Teil)
Quadratische Funktionen
Die Scheitelpunktform quadratischer Funktionen
Quadratische Funktionen: Scheitelpunktform und Normalform
Du kannst die Formen der Quadratischen Funktionen umwandeln:
Beispiel:
f(x) = (x + 3)² - 4 |1. binomische Formel
= x² + 2·x·3 + 3² - 4
= x² + 6x + 9 - 4
= x² + 6x + 5
Die Normalform eignet sich gut zur Nullstellenberechnung, denn hier kannst du die p-q-Formel anwenden.
Beispiel:
f(x) = x² + 8x - 4 |quadratische Ergänzung = 4² = 16
= x² + 8x + 16 - 16 - 4 |1. binomische Formel
= (x + 4)² - 16 - 4
= (x + 4)² - 20
Also lautet der Scheitelpunkt S(-4|-20)
Quadratische Funktionen: Nullstellen bestimmen
Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen.
Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen:
Tipp: Bestimme zunächst die Lage des Scheitelpunktes und die Öffnungsrichtung der Parabel. Ordne dann passend zu:
| keine | f(x) = x² + 3 | f(x) = -2x² - 5 | f(x) = (x+2)² + 1 |
| eine | f(x) = x² | f(x) = (x - 4)² | f(x) = -(x+2)² |
| zwei | f(x) = x² - 3 | f(x) = -2x² + 5 | f(x) = (x+2)² - 1 |
1. Form: f(x) = ax²
Beispiel: f(x) = 3x²
f(x) = 0
3x² = 0 |:3
x² = 0 |
x = 0
N(0|0)
Natürlich hat jede Parabel mit der Funktionsgleichung f(x) = ax² die Nullstelle N(0|0), denn ihr Scheitelpunkt liegt im Ursprung. Der Scheitelpunkt ist also die Nullstelle.
2. Form: f(x) = ax² + c
Beispiel: f(x) = 0,5x² - 8
f(x) = 0
0,5x² - 8 = 0 |+8
0,5x² = 8 |:0,5
x² = 16 |
x1 = - und x2 = +
x1 = -4 und x2 = +4
N1(-4|0) und N2(4|0)
3. Form: Scheitelpunktform f(x) = a(x+d)²+e
Beispiel: f(x) = 2(x + 2)² - 18
f(x) = 0
2(x + 2)² - 18 = 0 |+18
2(x + 2)² = 18 |:2
(x + 2)² = 9 |
x1 + 2 = - und x2 + 2 = +
x1 + 2 = -3 und x2 + 2 = 3 |-2
x1 = - 3 - 2 und x2 = + 3 - 2
x1 = -5 und x2 = 1
N1(-5|0) und N2(1|0)
Der Scheitelpunkt der Parabel liegt immer in der Mitte zwischen den beiden Nullstellen. Die x-Koordinate des Scheitelpunktes muss also -2 heißen. (x-Koordinate zwischen x = -5 und x = 1).
Dies passt zum Scheitelpunkt S(-2|-18), der aus der Parabelgleichung abgelesen werden kann.
4. Form: Normalform f(x) = x² + px + q
Lösung mit der p-q-Formel:
Normalform: f(x) = x² + px + q
x² + px + q = 0
x1/2 = -
Beispiel: f(x) = x² -6x + 5
f(x) = 0
x² - 6x + 5 = 0 | pq-Formel mit p=-6 und q=5
x1/2 = -
x1/2 = 3
x1/2 = 3
x1/2 = 32
x1 = 3 - 2 = 1 ; x2 = 3+2 = 5
N1(1|0) und N2(5|0)
4. Form: Normalform f(x) = x² + px + q (mit quadratischer Ergänzung )
Beispiel: f(x) = x² -6x + 5
f(x) = 0
x² - 6x + 5 = 0 | quadratische Ergänzung
x² - 6x + 3² - 3² + 5 = 0 | 2. binomische Formel
(x - 3)² - 9 + 5 = 0
(x - 3)² - 4 = 0 | nun hast du wieder die Scheitelpunktform und geht wie in Bsp 3 vor: +4
(x - 3)² = 4 |
x1 - 3 = -2 und x2 - 3 = 2 |+3
x1 = -2 + 3 und x2 = 2 + 3
x1 = 1 und x2 = 5
5. Form: allgemeine Form f(x) = ax² + bx + c
Wandle zunächst in die Normalform um.
Wende dann wieder die p-q-Formel an.
Beispiel: f(x) = 2x² + 12x + 10
f(x) = 0
2x² + 12x + 10 = 0 |:2 (Ziel: Normalform)
x² + 6x + 5 = 0 | pq-Formel mit p=6 und q=5
x1/2 = -
x1/2 = -3
x1/2 = -3
x1/2 = -32
x1 = -3 - 2 = -5 ; x2 = -3+2 = -1
N1(-5|0) und N2(-1|0)
Quadratische Funktionen: Funktionsgleichung aufstellen
Beispiel:
Eine Parabel hat den Scheitelpunkt S(0|-3) und geht durch den Punkt P(2|-2).
f(x) = a(x + d)² + e |Setze für d=0 und e=-3 ein
f(x) = a(x - 0)² + (-3)
f(x) = ax² - 3 |Setze die Koordinaten des Punkte P ein (Punktprobe)
-2 = a·2² - 3
-2 = 4a - 3 |+3
1 = 4a |:4
= a
Also lautet die Funktionsgleichung der Parabel f(x) = x² - 3.
Modellieren - Anwendungsaufgaben
Es gibt besondere Punkte, die in Anwendungen immer wieder von Bedeutung sind:
- Scheitelpunkt
- Nullstellen
- Schnittpunkt mit der y-Achse
- Koordinaten eines beliebigen Punktes
Verwende zur Lösung der Aufgabe die verschiedenen Darstellungsformen und die wiederholten Methoden zur Berechnung der verschiedenen besonderen Punkte.