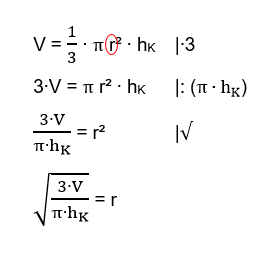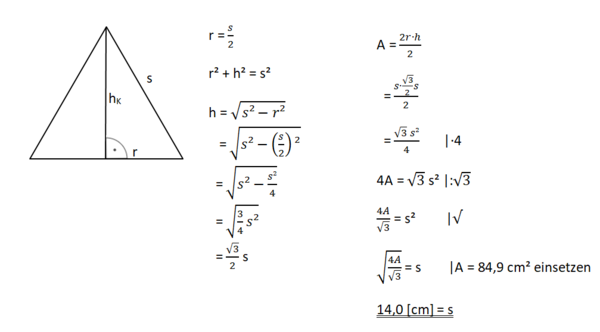Benutzer:Buss-Haskert/Körper/Kegel: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 59: | Zeile 59: | ||
{{Box|Übung 2| Bearbeite im Buch S. 50 oben die Bastelaufgabe und notiere deine Überlegungen in deinem Heft.|Üben}}<br> | {{Box|Übung 2| Bearbeite im Buch S. 50 oben die Bastelaufgabe und notiere deine Überlegungen in deinem Heft.|Üben}}<br> | ||
Originallink https://www.geogebra.org/m/JMBakasy | |||
<ggb_applet id="gATMx9BT" width="945" height="700" border="888888" /><br> | <ggb_applet id="gATMx9BT" width="945" height="700" border="888888" /><br> | ||
===3) Oberfläche von Kegeln=== | ===3) Oberfläche von Kegeln=== | ||
| Zeile 84: | Zeile 85: | ||
{{Lösung versteckt|1=[[Datei:Kegel Herleitung Formel Oberfläche 3.png|rahmenlos]]|2=Tipp 3 zur Herleitung der Formel|3=Verbergen}}<br> | {{Lösung versteckt|1=[[Datei:Kegel Herleitung Formel Oberfläche 3.png|rahmenlos]]|2=Tipp 3 zur Herleitung der Formel|3=Verbergen}}<br> | ||
<br> | <br> | ||
Ziehe den Punkt Schritt für Schritt weiter und erkläre, wie die Formel für die Oberfläche hergeleitet wird. | Ziehe den Punkt Schritt für Schritt weiter und erkläre, wie die Formel für die Oberfläche hergeleitet wird. <br> | ||
Originallink https://www.geogebra.org/m/sfazkjgc<br> | |||
<ggb_applet id="sfazkjgc" width="2200" height="2000" border="888888" /> | <ggb_applet id="sfazkjgc" width="2200" height="2000" border="888888" /> | ||
Applet von Buß-Haskert | Applet von Buß-Haskert | ||
| Zeile 169: | Zeile 171: | ||
{{Box|Volumen des Kegels|Du kannst die Formel für das Volumen eines Kegels auch mithilfe der Formel für die Pyramide herleiten. Eine weitere Möglichkeit ist die Annäherung durch Teilzylinder. Erkläre die folgenden GeoGebra-Applets.|Arbeitsmethode}} | {{Box|Volumen des Kegels|Du kannst die Formel für das Volumen eines Kegels auch mithilfe der Formel für die Pyramide herleiten. Eine weitere Möglichkeit ist die Annäherung durch Teilzylinder. Erkläre die folgenden GeoGebra-Applets.|Arbeitsmethode}} | ||
Originallink hwAXUV3B | Originallink https://www.geogebra.org/m/hwAXUV3B | ||
<ggb_applet id="hwAXUV3B" width="992" height="580" border="888888" /> | <ggb_applet id="hwAXUV3B" width="992" height="580" border="888888" /> | ||
<small>Applet von Wolfgang Wengler</small> | <small>Applet von Wolfgang Wengler</small> | ||
Aktuelle Version vom 27. Oktober 2024, 19:21 Uhr
2) Kegel
In der vorherigen Lerneinheit hast du die Pyramide mit einem beliebigen Vieleck als Grundfläche kennengelernt.
Ersetzt man nun das Vieleck der Grundfläche durch einen Kreis, so erhält man einen verwandten Spitzkörper: den Kegel!
 . . . .
. . . . . . . .
. . . .  . . . .
. . . . 
Ob Eistüte, Pylonen oder Turmspitzen, man findet sehr häufig kegelförmige Objekte in unserer Lebenswelt.
Originallink https://www.geogebra.org/m/XnTH43Qa

Applet von Martin Putzlocher
1) Merkmale von Kegeln
Ziehe an der Kegelspitze S und beobachte, was passiert.

von T.Weiss
2) Schrägbild und Netz von Kegeln
Das Video zeigt dir, wie du das Schrägbild eines Kegels zeichnest:
Originallink https://www.geogebra.org/m/HXWSPGTN

Applet von Andreas Lindner
Originallink https://www.geogebra.org/m/JMBakasy

3) Oberfläche von Kegeln
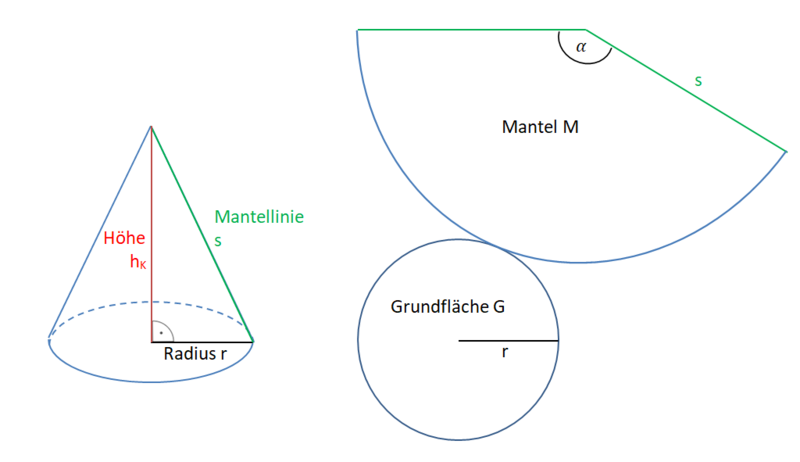
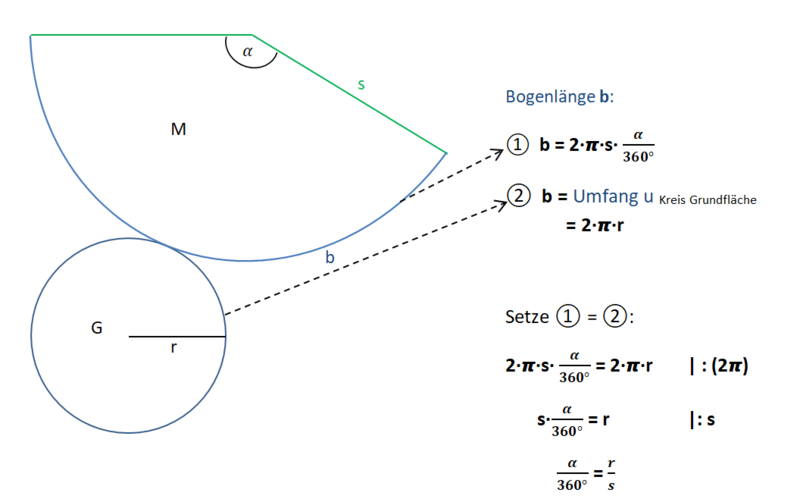
Die Grundfläche ist ein Kreis und die Mantelfläche hat die Form eines Kreisausschnittes.
Formel: O = G + M.
Das nachfolgende Applet kann dir helfen: Kippe den Kegel mit dem Schieberegler und führe die Abwicklung aus.(Du kannst Radius und Höhe des Kegels verändern.) Originallink https://www.geogebra.org/m/n8f5hnqb

Applet von Wolfgang Wengler Originallink https://www.geogebra.org/m/HXWSPGTN

Applet von Andreas Lindner
M= AKreisausschnitt (mit dem Radius s)
= 𝞹∙s²∙
aber: wir kennen α nicht
Ziehe den Punkt Schritt für Schritt weiter und erkläre, wie die Formel für die Oberfläche hergeleitet wird.
Originallink https://www.geogebra.org/m/sfazkjgc

Applet von Buß-Haskert
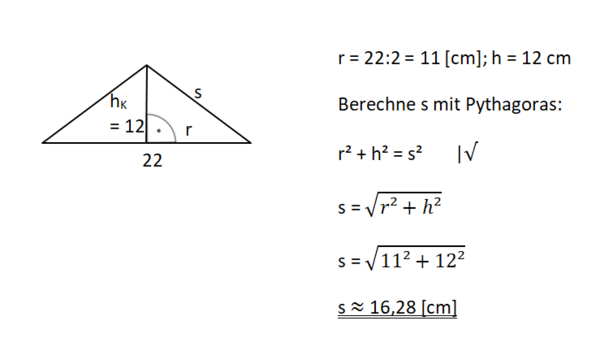
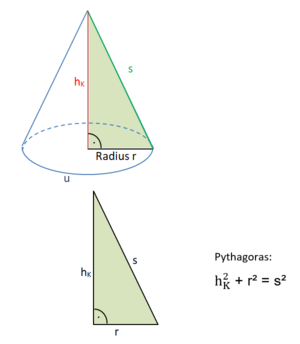
Wende zur Berechnungen der Längen r, hK oder s den Satz des Pythagoras im rechtwinkligen Hilfsdreieck mit den Katheten r und hK und der Hypotenuse s an.
Beispiel:
Umstellen der Mantelformel nach s:
M = 𝞹∙r∙s |:(𝞹∙r)
Setze die gegebenen Werte für M und r ein und berechne s.
Umstellen der Oberflächenformel nach s:
O = 𝞹∙r² + 𝞹∙r∙s |-𝞹∙r²
O - 𝞹∙r² = 𝞹∙r∙s |:(𝞹∙r)
Setze die gegebenen Werte für o und r ein und berechne s.
geg: s = 6,3 cm; O = 226 cm²
ges: r
O = 𝞹∙r² + 𝞹∙r∙s |Du musst also eine quadratische Gleichung lösen!
Setze die gegebenen Werte ein und bringe die Gleichung in die Normalform x² + px + q = 0 (hier ist r=x)
226 = 𝞹∙r² + 𝞹∙r∙6,3 |-226
0 = 𝞹∙r² + 𝞹∙r∙6,3 - 226 |:𝞹
0 = r² + 6,3∙r - 71,94 |pq-Formel mit p = 6,3 und q = -71,94
r1,2 = -3,15
Berechne die Länge des Weges, den er Kegel sich dreht. Dies ist der Umfang des Kreises mit dem Radius r=12cm.
Berechne dann den Umfang der Grundfläche des Kegels. Der Radius ist hier 5cm:2 = 2,5cm.
Lösung: 4,8 mal
Berechne zunächst die Oberfläche des Zylinders (O = 2G + M =2∙𝞹∙r² + 2∙𝞹∙r∙hK)
Berechne danach die Oberfläche des Zylinders.
Berechne nun den Unterschied zwischen den beiden Werten: OZylinder - OKegel
4) Volumen von Kegeln
Experimentelle Bestimmung der Volumenformel des Kegels
Du hast nun auf der Grundlage experimenteller Ergebnisse eine Formel für das Volumen eines Kegels aufgestellt.
Wie viele Kegelfüllungen passen in den Zylinder? _____
Also gilt:
VZylinder = ___∙ VKegel |umstellen nach VKegel
VKegel =___∙ VZylinder
Die Grundfläche G ist ein Kreis, also G = 𝞹∙r², setze in die Formel ein.
Originallink https://www.geogebra.org/m/hwAXUV3B

Applet von Wolfgang Wengler
Originallink https://www.geogebra.org/m/P7dYRTb8

Applet von Andreas Lindner
r² + hK² = s² |-r²
hK² = s² - r² |
r² + hK² = s² |-h²
r² = s² - hK² |
Umstellen der Formel nach hK:
V = ∙𝞹∙r²∙hK |∙3
3V = 𝞹∙r²∙hK |:(𝞹∙r²)
Das Volumen des Restkörpers beträgt des Volumens des ganzen Kegels, also
Oberfläche des Restkörpers beträgt der Oberfläche des ganzen Kegels, zusätzlich musst du die Flächen der zwei (rechtwinkligen) Dreiecke, die sich an den Schnittstellen ergeben, addieren.
Anwendungsaufgaben
Bestimme mithilfe des Mauerumfangs den Radius des Zylinders (Turm) r.
Das Dach steht 30 cm über, also gilt rDach = r + 0,3.
Wie geht Prozentrechung?
W = G · p%.
geg: G = Mantelfläche; p% = 3% (=0,03 als Dezimalbruch).
Berechne, wie viel Material hinzugegeben werden muss (W), und addiere dann W + G = G+
Oder berechne sofort G+
G = M und p+% = 103% = 1,03
Bestimme r mithilfe des angegebenen Umfangs u.
Bestimme das Volumen eines Kegels mit den angegebenen Maßen.
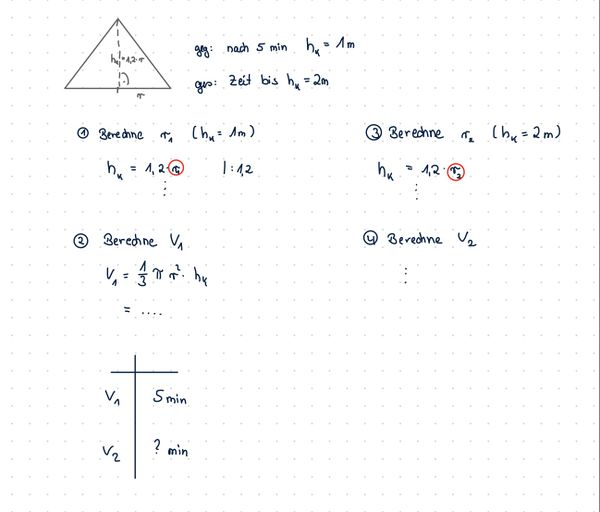
Bestimme V1 und V2.
Für die benötigte Zeit betrachte das Verhältnis von = ...
Die dementsprechend vielfache Zeit wird dann benötigt.
1. Bestimme das Volumen des Gewürzkegels. Entnimm die Maße dem Bild im Buch.
2. Bestimme das Volumen einer zylindrischen Dose.
Die Dichte von 7,8 gibt an, dass 1cm³ 7,8g wiegt.
Das Verhältnis von Radius zur Höhe bleibt gleich (Strahlensatz), also r = 1 cm und hK = 3; r = hK.
Noch mehr Übungen findest du auf der Seite Aufgabenfuchs - Kegel.