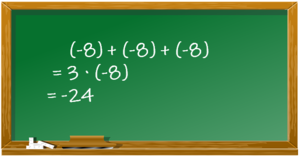Benutzer:Buss-Haskert/Einführung Rationale Zahlen/Rationale Zahlen multiplizieren und dividieren

zurück zur Seite der Herta-Lebenstein-Realschule

1) Einführung Rationale Zahlen
2) Vergleichen und ordnen von rationalen Zahlen
3) Rationale Zahlen im Koordinatensystem
4) Rationale Zahlen addieren und subtrahieren
5) Rationale Zahlen multiplizieren und dividieren
6) Verbindung der Rechenarten
7) Checkliste

5) Multiplizieren und Dividieren

5.1) Multiplikation und Division von ganzen Zahlen

Schau zunächst das einführende Video an:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Jana hat eine Aufgabe an der Tafel gerechnet:

Aufgabe 1
a) Gib eine Situation an, die zu Janas Rechnung passt (Tipp: Erinnere dich an die Situation im Video)
b) Beschreibe, wie sie bei ihrer Rechnung vorgegangen ist.
c) Löse ebenso:
  (-2)+(-2)+(-2)+(-2)
= ...
  (-5)+(-5)+(-5)
= ...
  (-3)+(-3)+(-3)+(-3)+(-3)+(-3)+(-3)+(-3)
=
d) Was fällt dir auf? Notiere im Heft und vergleiche dein Ergebnis mit dem deines Nachbarn.

Aufgabe 2
Nun sollst du an der Tafel rechnen:

a) Schreibe die Aufgabenfolgen in dein Heft und ergänze die Lücken.
b) Was fällt dir auf? Notiere im Heft und vergleiche dein Ergebnis mit dem deines Nachbarn.

Erinnerung: Kennst du dich aus mit den Fachbegriffen für die Multiplikation und Division? Löse das folgende Quiz:

1. Faktor ∙ 2. Faktor = Wert des Produktes
Beispiele:
3 ∙ 8 = 24
-3 ∙ (-8) = 24
3 ∙ (-8) = -24
-3 ∙ 8 = -24

Dividend : Divisor = Wert des Quotienten
Beispiele:
24 : 3 = 8
-24 : (-3) = 8
24 :(-3) = -8
-24 : 3 = -8

Multiplikation von rationalen Zahlen

Das Vorzeichen des Produktes ist abhängig von den Vorzeichen der einzelnen Faktoren.
Das Ergebnis ist positiv (+), wenn beide Faktoren die gleichen Vorzeichen haben.
Das Ergebnis ist negativ (-), wenn beide Faktoren verschiedene Vorzeichen haben.

Da die Division die Umkehrung der Multiplikation ist, gelten diese Regeln auch für die Division:

Division von rationalen Zahlen

Das Vorzeichen des Quotienten ist abhängig von den Vorzeichen von Dividend und Divisor.
Das Ergebnis ist positiv (+), wenn beide Zahlen die gleichen Vorzeichen haben.
Das Ergebnis ist negativ (-), wenn beide Zahlen verschiedene Vorzeichen haben.

Auch hier gilt also die bekannte Eselsbrücke:

Eselsbrücke:

+ ∙ (+) = +
- ∙ (-) = +
+ ∙ (-) = -

- ∙ (+) = -

+ : (+) = +
- : (-) = +
+ : (-) = -

- : (+) = -

Merke dir diese Regel mit dem Memoryspiel:

Wenn du zwei gleiche Karten aufdeckst, freust du dich (+),

also + ∙ (+) = + und - ∙ (-) = +
und + : (+) = + und - : (-) = +
wenn du verschiedene Karten aufdeckst, bist du traurig (-),
also + ∙ (-) = - und - ∙ (+) = -

und + : (-) = - und - : (+) = -

Zusammenfassende Videos:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1: Multiplikation

Löse die nachfolgenden LearningApps Nr. 1-5. Für die schnellen Rechner gibt es Sprinteraufgaben.

Übung 2: Division

Löse die nachfolgenden LearningApps Nr. 1-5. Für die schnellen Rechner gibt es Sprinteraufgaben.

Übung 3

Löse Buch

• S. 61 Nr. 1
• S. 62 Nr. 3
• S. 63 Nr. 1, 2
• S. 64 Nr. 3, 4, 5 und 6.

Bunte Mischung: -2009; -672; -360; -300; -72; -56; -36; – 35; +20; +60; +288; +901

Bunte Mischung:-12; -9 (2mal); -8 (4mal); -4; +5; +6; +7; +9

Bunte Mischung:-756; -300; -183; -84; -72; -23; -22; -19; -18; -13; -12; – 11; -8; -7; -6; +4; +8; +16; +18; +27; +84

Übung 4

Aufgaben mit mehreren Faktoren
Berechne

• a) 2∙3∙(-1)∙(-4)
• b) (-2)∙3∙(-1)∙(-4)
• c) (-2)∙(-2)∙(-2) = (-2)³
• d) (-2)∙(-2)∙(-2)∙(-2) = (-2)⁴
  

Was gilt für das Vorzeichen des Ergebnisses? Beschreibe deine Beobachtung und vergleiche deine Lösung mit der deines Nachbarn.

a) +24; b) -24; c) -8; d) +16

Das Vorzeichnen des Ergebnisses hängt ab von der Anzahl der negativen Faktoren.

Das Vorzeichnen des Ergebnisses hängt ab von der Anzahl der negativen Faktoren:
Ist die Anzahl gerade, so ist das Ergebnis positiv.

Ist die Anzahl ungerade, so ist das Ergebnis negativ.

5.2) Multiplikation und Division von rationalen Zahlen (Dezimalbrüche)

Die Vorzeichenregeln gelten natürlich auch für die Multiplikation und Division von Dezimalbrüchen.
Erinnerung: Dezimalbrüche multiplizieren
Dezimalbrüche werden multipliziert, indem die Zahlen zunächst ohne Berücksichtigung des Kommas multipliziert werden. Dann setzt man das Komma im Ergebnis. Das Ergebnis hat so viele Nachkommastellen, wie beide Faktoren zusammen.
(Ausführlich kannst du die Multiplikation von Dezimalbrüchen hier wiederholen.)
Zusammenfassende Videos:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 5: Multiplikation von rationalen Zahlen (Dezimalbrüche)

Löse die nachfolgenden LearningApps Nr. 1-3. Für die schnellen Rechner gibt es Sprinteraufgaben.

Erinnerung: Dezimalbrüche dividieren
Beim Dividieren von Dezimalbrüchen durch eine ganze Zahl wird das Ergebnis im Komma gesetzt, sobald das Komma beim Dividenden überschritten wird. Ist der Divisor auch ein Dezimalbruch, müssen zunächst beim Dividenden und beim Divisor das Komma um so viele Stellen nach rechts verschoben werden, bis der Divisor eine natürliche Zahl ist.
(Ausführlich kannst du die Division von Dezimalbrüchen https://projekte.zum.de/wiki/Herta-Lebenstein-Realschule/Lernpfad_Rechnen_mit_Dezimalbr%C3%BCchen/3)_Dezimalbr%C3%BCche_dividieren hier] wiederholen.)

Übung 6: Division von rationalen Zahlen (Dezimalbrüche)

Löse die nachfolgenden LearningApps Nr. 1-3. Für die schnellen Rechner gibt es Sprinteraufgaben.

5.3) Multiplikation und Division von rationalen Zahlen (Brüche)

Und schlussendlich gelten die Vorzeichenregeln natürlich auch für die Multiplikation und Division von Brüchen.
Erinnerung: Brüche multiplizieren
Brüche werden multipliziert, indem Zähler mit Zähler und Nenner mit Nenner multipliziert werden. Denke daran, zuerst zu kürzen und dann das Ergebnis zu berechnen.
(Ausführlich kannst du die Multiplikation von Brüchen auf der Seite Grundwissen - Brüche unten wiederholen und üben.) Zusammenfassende Videos:

Übung 7: Multiplikation von rationalen Zahlen (Brüche)

Löse die nachfolgenden LearningApps Nr. 1-3. Für die schnellen Rechner gibt es Sprinteraufgaben.

Erinnerung: Brüche dividieren
Brüche werden dividiert, indem der erste Bruch mit dem Kehrbruch des zweiten Bruches multipliziert wird. ("Schweinchenlied")
(Ausführlich kannst du die Division von Brüchen Grundwissen Brüche unten wiederholen und üben.)

Übung 8

Löse Buch

• S. 61 Nr. 2
• S. 62 Nr. 6
• S. 64 Nr. 7
• S. 64 Nr. 8

Zwischentest 5

Bist du fit?

Hast du alle Hefteinträge abgeschrieben und alle Aufgaben gelöst? Dann bearbeite den Test 5. Du erhältst ihn von deiner Lehrerin.
Bearbeite den Test allein. Kontrolliere deine Ergebnisse mit den Musterlösungen.

Wie viele Punkte hast du erreicht? Wähle den passenden Link unten aus.

0-6P: Wiederholung: Brüche multiplizieren und dividieren: Aufgabenfuchs Aufgabe 52-58

7-9P: weiter zur Checkliste
BUNTE MISCHUNG: Wähle die Rechenart, die du üben möchtest, aus.

Aufgabenfuchs Aufgabe 59-60

6) Checkliste