Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (28 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
{{Fortsetzung|vorher=zurück zur Übersicht Vorbereitungskurs ZP 10|vorherlink=Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik}}<br> | |||
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag | |||
{{Navigation verstecken|[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Größen| 1. Zahlen und Größen]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Zuordnungen|2. Zuordnungen und Prozent-und Zinsrechnung]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Gleichungen|3. Terme und Gleichungen (lineare Gleichungen, lineare Gleichungssysteme (LGS) und quadratische Gleichungen)]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen|4. Funktionen: Lineare Funktionen]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen Teil2|5. Funktionen: Quadratische Funktionen]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie|6. Geometrie: Winkel in Figuren; Flächen- und Körperberechnungen; Pythagoras, Strahlensätze, Trigonometrie]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik|7. Diagramme, Statistik]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit|8. Wahrscheinlichkeitsrechnung]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Exponentiafunktion|9. Wachstum und Exponentialfunktion]] | |||
}} | |||
==Statistik== | ==Statistik== | ||
====Einstiegstest: Diagramme, Statistik==== | |||
<quiz display="simple"> | |||
{In einer Klasse kommen 5 Schüler*innen zu Fuß, 12 mit dem Bus und 8 mit dem Fahrrad. Gib die relative Häufigkeit der Schüler*innen an, die mit dem Fahrrad kommen.} | |||
- 8 | |||
- 0,8 | |||
- 8% | |||
+ 32% | |||
- 28% | |||
{In welchem Diagramm ist die Verteilung der Beförderungsmittel richtig dargestellt (zu den Angaben oben)? | |||
[[Datei:Kreisdiagramme Beförderungsmittel Schulweg.png|rahmenlos|400x400px]]} | |||
- A | |||
+ B | |||
- C | |||
{Das arithmetische Mittel ist...} | |||
- der Abstand zwischen Minimum und Maximum | |||
- der Wert, der in der Datenreihe am häufigsten vorkommt | |||
+ die Summe aller Werte geteilt durch die Anzahl der Werte | |||
- der mittlere Wert einer geordneten Rangliste | |||
{Die Hälfte aller Werte einer Rangliste ist größer oder gleich groß wie der Median.} | |||
+ Ja, das stimmt. | |||
- Nein, das stimmt nicht. | |||
{In einer Klasse haben einige Schülerinnen und Schüler (17 Jahre) die Höhe ihrer monatlichen Handykosten notiert. | |||
5€; 10€; 10€; 10€; 10€; 15€; 20€; 25€; 25€; 30€; 50€ | |||
Welche angegebenen Kenngrößen wurden richtig berechnet?} | |||
+ arithmetisches Mittel <math>\bar{x}</math> ≈ 19,10€ | |||
- arithmetisches Mittel <math>\bar{x}</math> = 20,00€ | |||
- Zentralwert (Median) Z = 19,10€ | |||
+ Zentralwert (Median) Z = 15,00€ | |||
+ Spannweite w = 45,00€ | |||
- Spannweite w = 15,00€ | |||
- Modalwert m = 25,00€ | |||
+ Modalwert m = 10,00€ | |||
{Welche der Aussagen zu den Boxplots sind richtig? | |||
[[Datei:Boxplot monatliche Handykosten.png|rahmenlos|600x600px]]} | |||
- Die durchschnittlichen Handykosten für die 8-16 Jährigen betragen 7,50€. | |||
+ Die Hälfte aller 8-16 Jährigen gibt im Monat zwischen 5€ und 15€ für das Handy aus. | |||
+ Die Hälfte aller 17-25 Jährigen gibt im Monat mindestens 15€ aus. | |||
+ Das untere Quartil beträgt für die 17-25 Jährigen 10€. | |||
</quiz> | |||
{{Box|Auswertung des Eingangstests|Schau, welche Aufgaben du schon gut lösen konntest und bei welchen du noch Schwierigkeiten hattest. Übe dann passend. | |||
* Häufigkeiten und Diagramme Nr. 1,2 | |||
* Statistische Kenngrößen Nr. 3-5 | |||
* Boxplot Nr. 6|Lösung}} | |||
{{Box|Übung|Löse die Aufgaben aus dem Buch und vergleiche deine Lösungen mit denen hinten im Buch.<br> | |||
Häufigkeiten und Diagramme: | |||
* S. 134, P1 - P4 | |||
* S. 135, P5 - P8 | |||
* S. 136, P 9 | |||
* S. 161, Nr. 1-3 | |||
Kenngrößen und Boxplots: | |||
* S. 136, P10 und P11 | |||
* S. 137, P12-P14 | |||
* S. 162, Nr. 1-3|Üben}} | |||
===Häufigkeiten=== | ===Häufigkeiten=== | ||
Absolute und relative Häufigkeit<br> | Absolute und relative Häufigkeit<br> | ||
| Zeile 120: | Zeile 197: | ||
{{#ev:youtube|uhIhG8uHS00|420|center}}</div> | {{#ev:youtube|uhIhG8uHS00|420|center}}</div> | ||
</div> | </div> | ||
| Zeile 164: | Zeile 235: | ||
{{!)}} | {{!)}} | ||
'''Ordne die mathematischen Bezeichnungen und Formeln richtig zu.''' | |||
<div class="zuordnungs-quiz"> | |||
{| | |||
|arithmetisches Mittel||Durchschnitt||Mittelwert||<math>\bar{x}</math>||<math>\bar{m}</math> | |||
|- | |||
|Median||Zentralwert||<math>x_{Med}</math>||der mittlere Wert eines sortierten Urliste||Z | |||
|- | |||
|Modus||<math>x_{Mod}</math>||der häufigste Wert||Modalwert||m | |||
|} | |||
</div> | |||
{{Box|Kennwerte - Beispiel Körpergrößen|Die Liste gibt die Körpergröße von 11 Personen an. Bestimme die statistischen Kennwerte und zeichne einen Boxplot.|Lösung}} | |||
Urliste (ungeordnet): 181cm; 159cm; 167cm; 170cm; 169cm; 184cm; 171cm; 177cm; 175cm; 177cm; 172cm<br> | |||
*1. Schritt: Erstelle eine Rangliste: Ordne die Werte der Größe nach. | |||
Rangliste: 159cm; 167cm; 169cm; 170cm; 171cm; 172cm; 175cm; 177cm; 177cm; 181cm; 188cm<br> | |||
*2. Schritt: Ermittle die Kennwerte:<br> | |||
Minimum: 159cm<br> | |||
Maximum: 188cm<br> | |||
Spannweite: w = 188cm - 159cm = 29cm<br> | |||
Median/Zentralwert: Es gibt n=11 Werte, also befindet sich der Median auf dem 6. Rangplatz.<br> | |||
(n:2 = 11:2 = 5,5; also 6. Rang)<br> | |||
Auf dem 6. Rangplatz steht 172cm, also ist Z = 172cm<br> | |||
unteres Quartil: Median der unteren Hälfte, also befindet sich der Wert des unteren Quartils auf dem 3. Rangplatz.<br> | |||
(n:4 = 11:4 = 2,75; also 3. Rang).<br> | |||
Auf dem 3. Rangplatz steht 169cm, also ist q<sub>u</sub> = 169cm<br> | |||
oberes Quartil: Median der oberen Hälfte, also befindet sich der Wert des unteren Quartils auf dem 3. Rangplatz.<br> | |||
(n·<math>\tfrac{3}{4}</math> = 11·<math>\tfrac{3}{4}</math> = 8,25; also 9. Rang).<br> | |||
Auf dem 9. Rangplatz steht 177cm, also ist q<sub>u</sub> = 177cm<br> | |||
Quartilabstand: 177cm - 169cm = 8cm<br> | |||
Mittelwert: <math>\bar{m}</math> = <math>\tfrac{159 + 167 + 169 + 170 + 171 + 172 + 175 + 177 + 177 + 181 + 188}{11}</math> ≈ 173,3<br> | |||
Modus (Modalwert): m = 177cm (Dieser Wert kommt am häufigsten vor, nämlich zweimal.)<br> | |||
<br> | |||
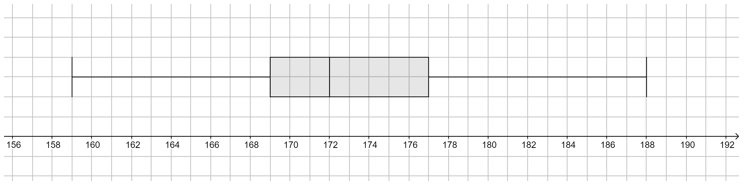
Boxplot:<br> | |||
[[Datei:Boxplot (Körpergröße) neu.png|rahmenlos|800x800px]]<br> | |||
===Boxplots=== | ===Boxplots=== | ||
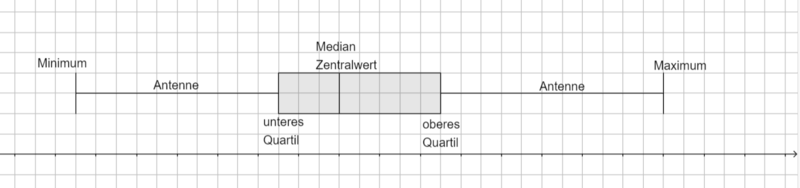
{{Box|Boxplot|Die statistischen Kenngrößen Minimum, Maximum, Median und die Quartile können in einem Boxplot dargestellt werden.<br>[[Datei:Boxplot Bezeichnungen.png|rahmenlos|800x800px]]<br> | |||
Der Boxplot gibt einen Überblick, wie sich die Daten verteilen. Die Datenmenge wird Hälften bzw. Viertel eingeteilt:<br> | |||
* 50% der Daten liegen in der Box (zentrale Hälfte). | |||
* 50% der Daten sind kleiner oder gleich groß wie der Median. | |||
* 50% der Daten sind größer oder gleich groß wie der Median. | |||
* 25% der Daten liegen zwischen dem Minimum und dem unteren Quartil, usw. | |||
* Die Spannweite entspricht der Breite des gesamten Boxplots. | |||
* Ist der Boxplot bzw. die Box sehr klein/eng, liegen die Daten dicht beieinander.|Merksatz}} | |||
{{#ev:youtube|ttz7Oo-7NhA|420|center}} | {{#ev:youtube|ttz7Oo-7NhA|420|center}} | ||
Aktuelle Version vom 17. September 2023, 17:32 Uhr
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag
Statistik
Einstiegstest: Diagramme, Statistik
Häufigkeiten
Absolute und relative Häufigkeit
Im Unterricht haben wir diese Begriffe eingeführt mit den Würfen auf einen Eimer. Die Jungen durften 20 mal werfen, die Mädchen 25 mal. Gezählt wurden dann die Treffer.
Wir ergänzen die Tabelle:
| Name | Mats | Lisa | Kassem | Ida | Larissa | Henry | |
|---|---|---|---|---|---|---|---|
| Würfe insgesamt | 20 | 25 | 20 | 25 | 25 | 20 | |
| Absolute Häufigkeit | Treffer | 10 | 11 | 13 | 12 | 16 | 12 |
| Relative Häufigkeit |
|
① Absolut gesehen hat LARISSA die meisten Treffer.
② Für den relativen Vergleich müssen wir die Anteile betrachten.
| Name | Bruch | Dezimalbruch | Prozent |
|---|---|---|---|
| Mats | = | 0,5 | 50% |
| Lisa | = | 0,44 | 44% |
| Kassem | = | 0,65 | 65% |
| Ida | = | 0,48 | 48% |
| Larissa | = | 0,64 | 64% |
| Henry | = | 0,6 | 60% |
Kassem hat also gewonnen, denn 65 % seiner Würfe haben den Eimer getroffen.
Larissa hatte zwar absolut gesehen mehr Treffer aber „nur“ 64% ihrer Würfe haben den Eimer getroffen.
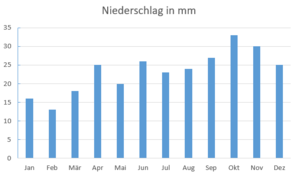
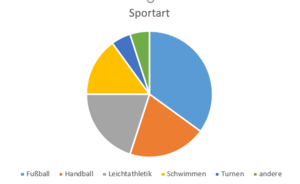
Diagramme
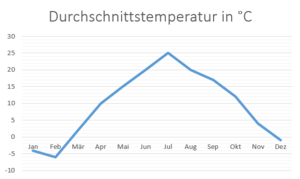
Liniendiagramm
Statistische Kennwerte
Werden in einer statistischen Erhebung Daten gesammelt (z.B. die verschiedenen Körpergrößen in einer Klasse), werden diese mithilfe von Kennwerten ausgewertet.
Die Daten werden zunächst in einer Urliste gesammelt. Ordnet man die Werte der Größe nach, so erhält man eine Rangliste.
| Kennwert | Bedeutung |
|---|---|
| Minimum | kleinster Wert |
| Maximum | größter Wert |
| Spannweite | Differenz aus Maximum und Minimum |
| Median/Zentralwert | Wert in der Mitte der Rangliste |
| unteres Quartil | Median der unteren Hälfte |
| oberes Quartil | Median der oberen Hälfte |
| Quartilabstand | Differenz aus oberem und unterem Quartil |
| Mittelwert (arithmetisches Mittel) | "Durchschnitt": Summe aller Werte geteilt durch Anzahl der Werte |
Ordne die mathematischen Bezeichnungen und Formeln richtig zu.
| arithmetisches Mittel | Durchschnitt | Mittelwert | ||
| Median | Zentralwert | der mittlere Wert eines sortierten Urliste | Z | |
| Modus | der häufigste Wert | Modalwert | m |
Urliste (ungeordnet): 181cm; 159cm; 167cm; 170cm; 169cm; 184cm; 171cm; 177cm; 175cm; 177cm; 172cm
- 1. Schritt: Erstelle eine Rangliste: Ordne die Werte der Größe nach.
Rangliste: 159cm; 167cm; 169cm; 170cm; 171cm; 172cm; 175cm; 177cm; 177cm; 181cm; 188cm
- 2. Schritt: Ermittle die Kennwerte:
Minimum: 159cm
Maximum: 188cm
Spannweite: w = 188cm - 159cm = 29cm
Median/Zentralwert: Es gibt n=11 Werte, also befindet sich der Median auf dem 6. Rangplatz.
(n:2 = 11:2 = 5,5; also 6. Rang)
Auf dem 6. Rangplatz steht 172cm, also ist Z = 172cm
unteres Quartil: Median der unteren Hälfte, also befindet sich der Wert des unteren Quartils auf dem 3. Rangplatz.
(n:4 = 11:4 = 2,75; also 3. Rang).
Auf dem 3. Rangplatz steht 169cm, also ist qu = 169cm
oberes Quartil: Median der oberen Hälfte, also befindet sich der Wert des unteren Quartils auf dem 3. Rangplatz.
(n· = 11· = 8,25; also 9. Rang).
Auf dem 9. Rangplatz steht 177cm, also ist qu = 177cm
Quartilabstand: 177cm - 169cm = 8cm
Mittelwert: = ≈ 173,3
Modus (Modalwert): m = 177cm (Dieser Wert kommt am häufigsten vor, nämlich zweimal.)
Boxplot: