Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
{{Fortsetzung|vorher=zurück zur Übersicht Vorbereitungskurs ZP 10|vorherlink=Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik}}<br> | {{Fortsetzung|vorher=zurück zur Übersicht Vorbereitungskurs ZP 10|vorherlink=Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik}}<br> | ||
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag | |||
{{Navigation verstecken|[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | {{Navigation verstecken|[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Größen| 1. Zahlen und Größen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Zuordnungen|2. Zuordnungen und Prozent-und Zinsrechnung]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Gleichungen|3. Terme und Gleichungen (lineare Gleichungen, lineare Gleichungssysteme (LGS) und quadratische Gleichungen)]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/ | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen|4. Funktionen: Lineare Funktionen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen Teil2|5. Funktionen: Quadratische Funktionen]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Geometrie|6. Geometrie: Winkel in Figuren; Flächen- und Körperberechnungen; Pythagoras, Strahlensätze, Trigonometrie]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit| | [[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik|7. Diagramme, Statistik]]<br> | ||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Wahrscheinlichkeit|8. Wahrscheinlichkeitsrechnung]]<br> | |||
[[Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Exponentiafunktion|9. Wachstum und Exponentialfunktion]] | |||
}} | }} | ||
| Zeile 109: | Zeile 111: | ||
* Punktprobe Nr. 10 | * Punktprobe Nr. 10 | ||
* Nullstellen Nr. 11|Lösung}} | * Nullstellen Nr. 11|Lösung}} | ||
{{Box|Übung|Löse die Aufgaben aus dem Buch, vergleiche deine Lösungen. Nutze zur Wiederholung die Zusammenfassungen in diesem Lernpfad. | |||
* Lineare Funktionen erkennen: S. 150, Nr. 1,2 | |||
* Lineare Funktionen zeichnen: S. 150, Nr. 3,4 | |||
* Gleichung - Graph: S. 150, Nr. 5,6 und S. 122, P2 - 4 | |||
* Schnittpunkte mit den Koordinatenachsen: S. 122, P5 - 6 | |||
* Punktprobe: S. 122(123, P7 - P10|Üben}} | |||
| Zeile 244: | Zeile 253: | ||
{{#ev:youtube|bE-yJzIqeIU|800|center}}|2=Video: Zwei-Punkteform der Geradengleichung|3=Verbergen}} | {{#ev:youtube|bE-yJzIqeIU|800|center}}|2=Video: Zwei-Punkteform der Geradengleichung|3=Verbergen}} | ||
===Lineare Funktionen: Punktprobe=== | |||
{{Box|1=Punktprobe|2=Wir können rechnerisch prüfen, ob ein Punkt auf dem Graphen der Funktion liegt. Dazu setzen wir die Koordinaten des Punktes P(<span style="color:red">x</span>I<span style="color:blue">y</span>) in die Funktionsgleichung <span style="color:blue">f(x)</span> = m<span style="color:red">x</span> + b ein. Der Punkt liegt auf dem Graphen, wenn sich eine wahre Aussage ergibt, die Gleichung also erfüllt ist.|3=Merksatz}} | {{Box|1=Punktprobe|2=Wir können rechnerisch prüfen, ob ein Punkt auf dem Graphen der Funktion liegt. Dazu setzen wir die Koordinaten des Punktes P(<span style="color:red">x</span>I<span style="color:blue">y</span>) in die Funktionsgleichung <span style="color:blue">f(x)</span> = m<span style="color:red">x</span> + b ein. Der Punkt liegt auf dem Graphen, wenn sich eine wahre Aussage ergibt, die Gleichung also erfüllt ist.|3=Merksatz}} | ||
{{LearningApp|app= ppkr9n4sj20|width=100%|height=400px}} | {{LearningApp|app= ppkr9n4sj20|width=100%|height=400px}} | ||
Aktuelle Version vom 4. Juli 2023, 06:13 Uhr
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag
Funktionen
Einstiegstest: Lineare Funktionen (hilfsmittelfreier Teil)
Lineare Funktionen erkennen
Diese Eigenschaften werden in folgendem Lied besungen.
Hier heißt die Funktionsgleichung f(x) = mx + n (n statt b, du findest in verschiedenen Büchern verschiedene Bezeichnungen).
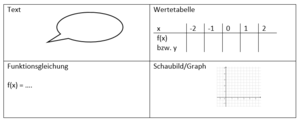
Lineare Funktionen: Wertetabelle
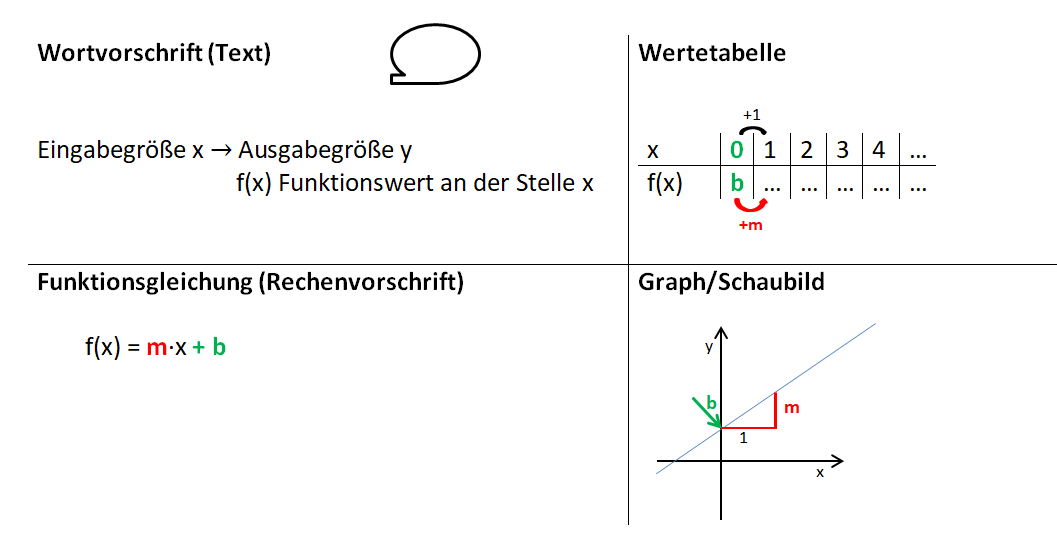
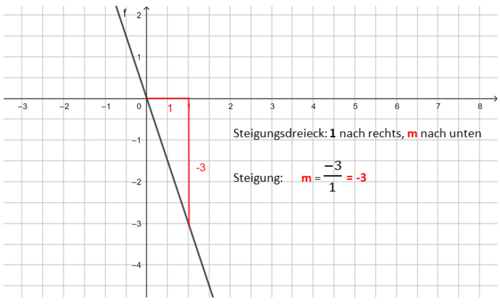
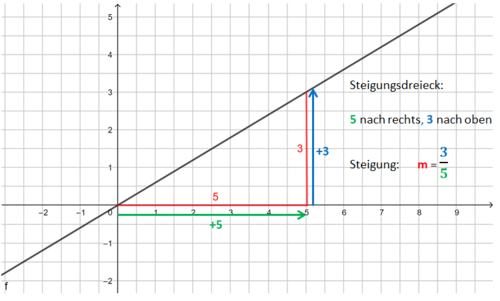
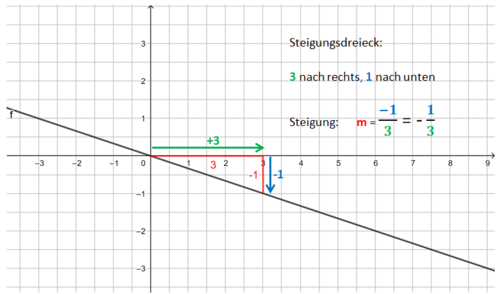
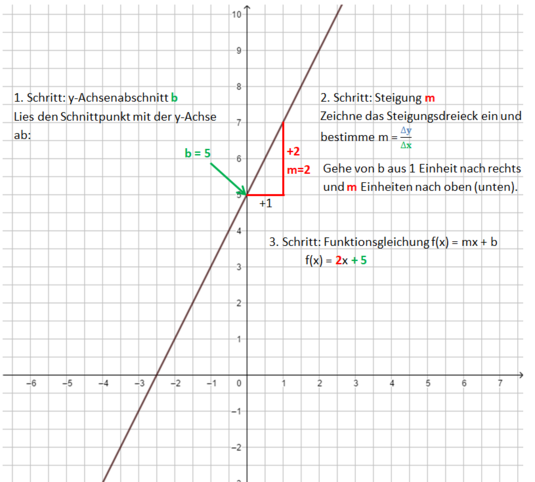
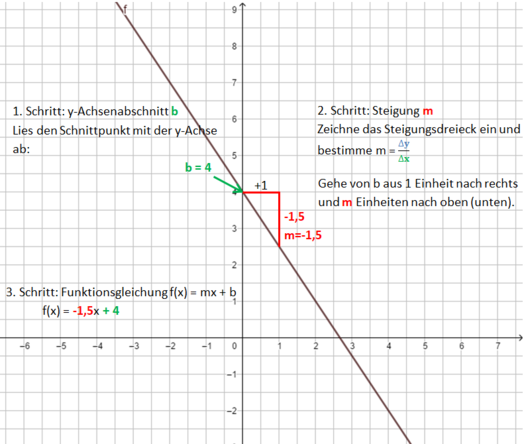
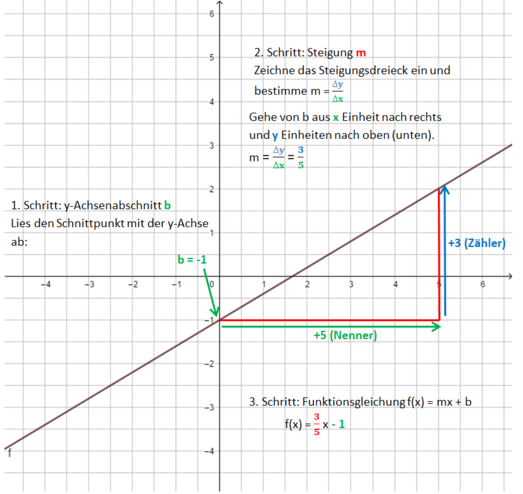
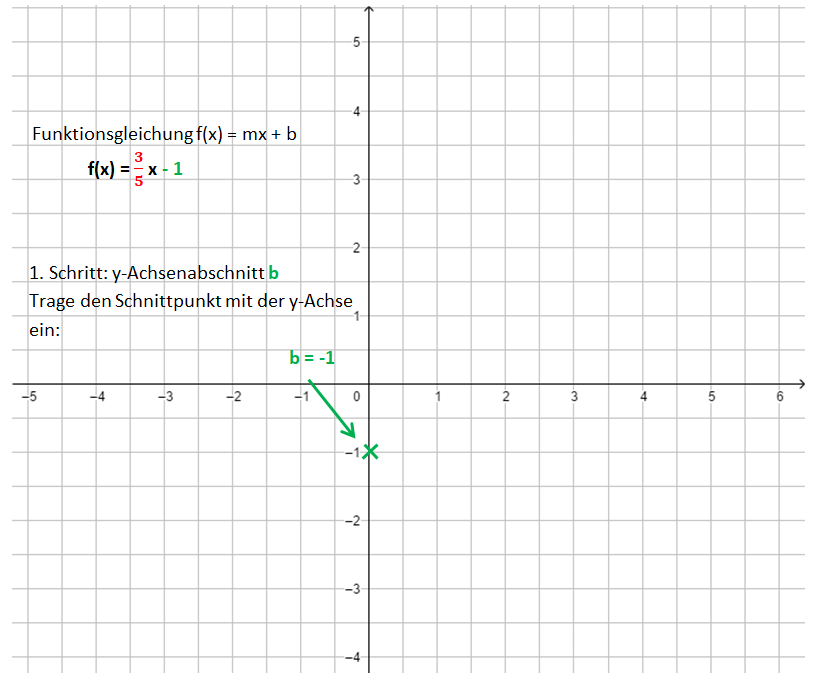
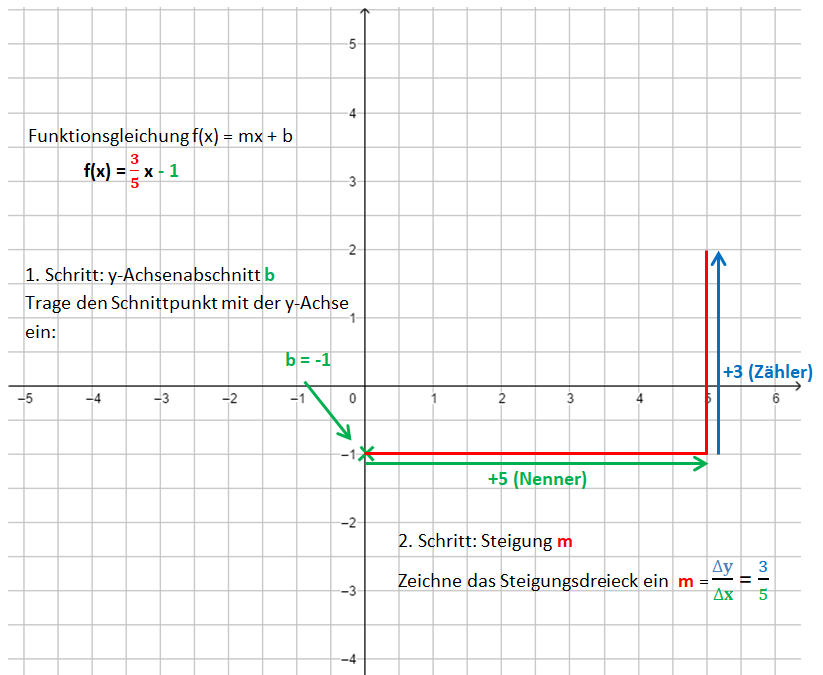
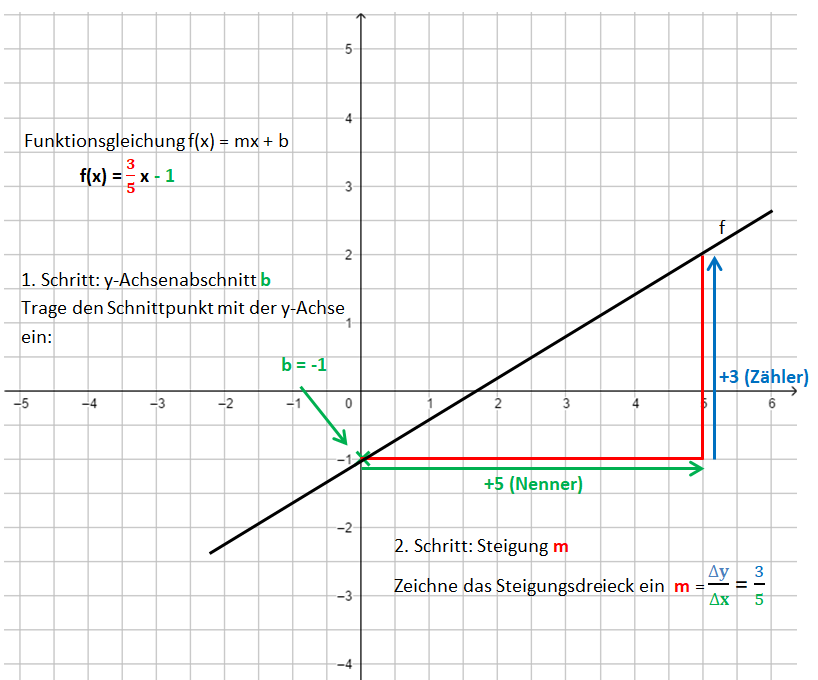
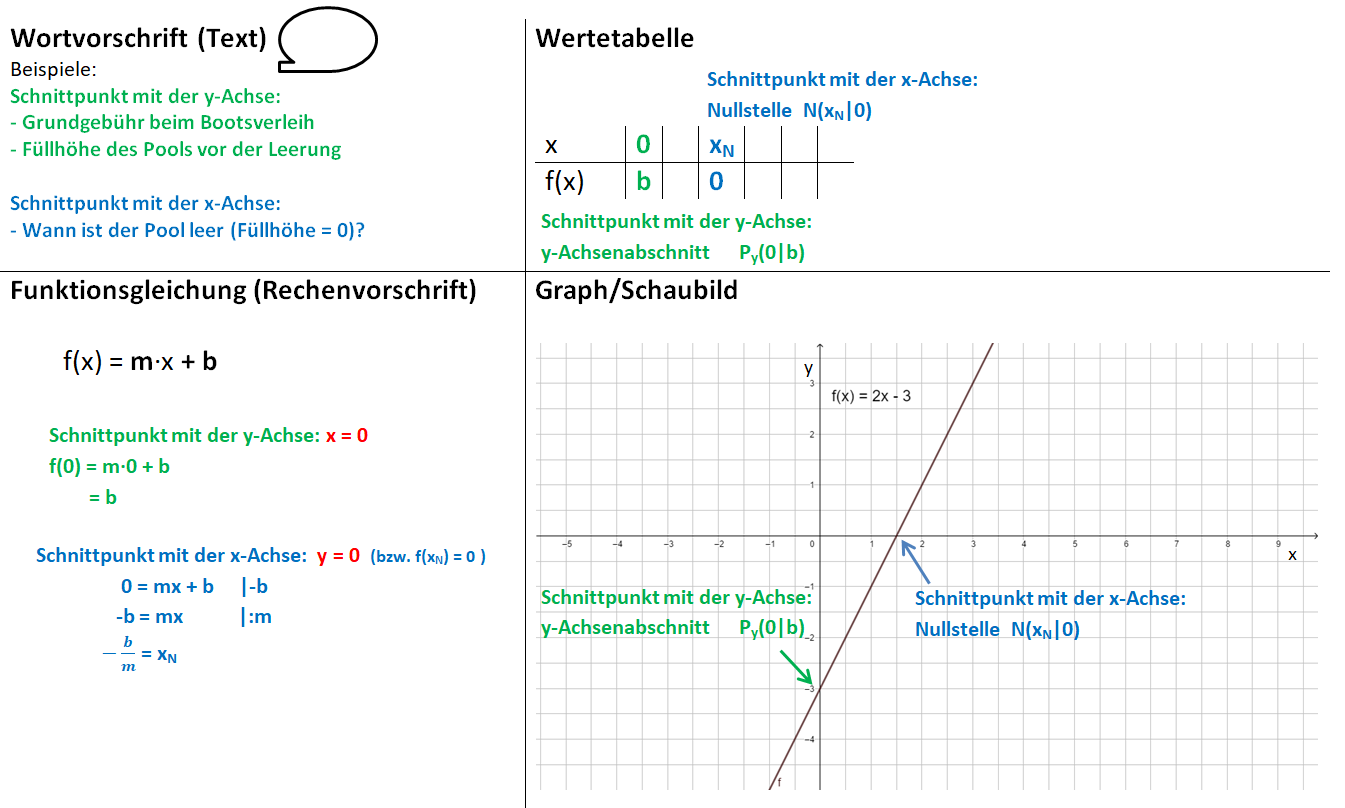
Lineare Funktionen: Gleichung und Graph
Beispiele:
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Lineare Funktionen: Funktionsgleichung rechnerisch bestimmen
Beispiel 1: Punkt-Steigungsform
geg: m = -1 und P(2|3)
ges: Funktionsgleichung der linearen Funktion
Idee: Setze m und die Koordinaten des Punktes in die Gleichung y = mx + b ein und bestimme so b.
f(x) = mx + b |m=-1 und P(2|3) einsetzen
3 = -1·2 + b |vereinfachen
3 = -2 + b |+2
5 = b
Also lautet die Funktionsgleichung f(x) = -1x + 5.
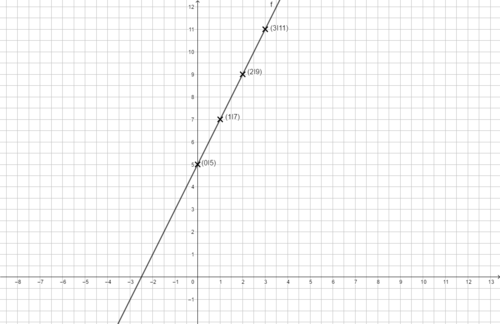
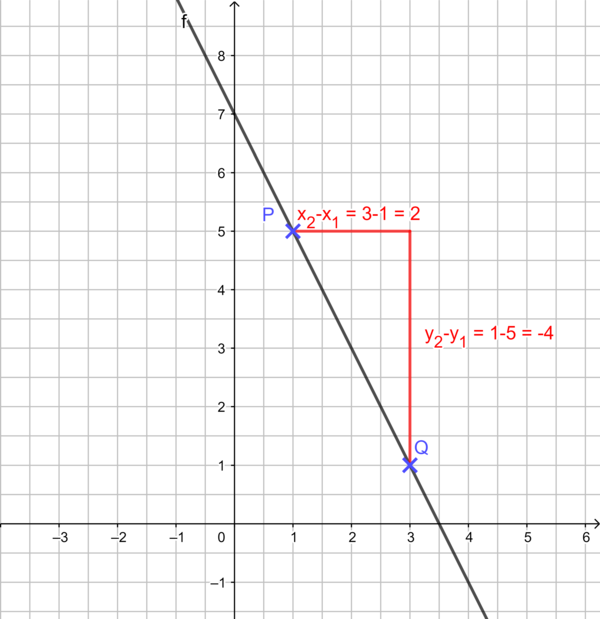
Beispiel 2: Zwei-Punkte-Form
geg: P(1|5) und Q(3|1)
ges: Funktionsgleichung der linearen Funktion
Bestimme die Steiung m: m = = = = -2
Bestimme b durch Einsetzen von m und einem der Punkte P oder Q in die Gleichung y = mx + b.
f(x) = mx + b |m=-2 und P(1|5) einsetzen
5 = -2·1 + b |vereinfachen
5 = -2 + b |+2
7 = b
Also lautet die Funktionsgleichung f(x) = -2x + 7.
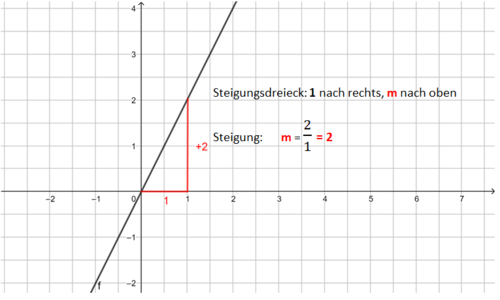
Erkläre, wie du das Steigungsdreieck zwischen den Punkten P und Q einzeichnen kannst und wie du damit die Steigung m bestimmen kannst.
Lineare Funktionen: Punktprobe
Lineare Funktionen: Nullstellen bestimmen