Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik: Unterschied zwischen den Versionen

Version vom 11. März 2023, 12:29 Uhr

zurück zur Seite der Herta-Lebenstein-Realschule

zurück zur Übersicht Vorbereitungskurs ZP 10

Statistik

Einstiegstest: Diagramme, Statistik

Auswertung des Eingangstests

Schau, welche Aufgaben du schon gut lösen konntest und bei welchen du noch Schwierigkeiten hattest. Übe dann passend.

Absolute und relative Häufigkeit Nr. 1,2
Statistische Kenngrößen Nr. 3-5
Boxplot Nr. 6

Häufigkeiten

Absolute und relative Häufigkeit

Häufigkeiten

Die absolute Häufigkeit gibt an, wie oft ein bestimmter Wert in einer statistischen Erhebung vorkommt.
Die relative Häufigkeit gibt den Anteil an: relative Häufigkeit =

\frac{\text{absolute Häufigkeit}}{\text{Gesamtzahl}}

.

Im Unterricht haben wir diese Begriffe eingeführt mit den Würfen auf einen Eimer. Die Jungen durften 20 mal werfen, die Mädchen 25 mal. Gezählt wurden dann die Treffer.

Absolute und relative Häufigkeit

Die Anzahl der Treffer heißt absolute Häufikgeit.

Schauen wir nach dem Anteil der Treffer, also wie viele Treffer es bei wie vielen Würfen gab, so heißt dies relative Häufigkeit.

Wir ergänzen die Tabelle:

	Name	Mats	Lisa	Kassem	Ida	Larissa	Henry
	Würfe insgesamt	20	25	20	25	25	20
Absolute Häufigkeit	Treffer	10	11	13	12	16	12
Relative Häufigkeit	$\frac{\text{Anzahl der Treffer}}{\text{Anzahl der Würfe insgesamt}}$	$\tfrac{10}{20}$	$\tfrac{11}{25}$	$\tfrac{13}{20}$	$\tfrac{12}{25}$	$\tfrac{16}{25}$	$\tfrac{12}{20}$

① Absolut gesehen hat LARISSA die meisten Treffer.

② Für den relativen Vergleich müssen wir die Anteile $\frac{\text{Anzahl der Treffer}}{\text{Anzahl der Würfe insgesamt}}$ betrachten.

Name	Bruch	Dezimalbruch	Prozent
Mats	$\tfrac{10}{20}$ = $\tfrac{50}{100}$	0,5	50%
Lisa	$\tfrac{11}{25}$ = $\tfrac{44}{100}$	0,44	44%
Kassem	$\tfrac{13}{20}$ = $\tfrac{65}{100}$	0,65	65%
Ida	$\tfrac{12}{25}$ = $\tfrac{48}{100}$	0,48	48%
Larissa	$\tfrac{16}{25}$ = $\tfrac{64}{100}$	0,64	64%
Henry	$\tfrac{12}{20}$ = $\tfrac{60}{100}$	0,6	60%

Kassem hat also gewonnen, denn 65 % seiner Würfe haben den Eimer getroffen.
Larissa hatte zwar absolut gesehen mehr Treffer aber „nur“ 64% ihrer Würfe haben den Eimer getroffen.

Diagramme

Arten von Diagrammen

Je nachdem, was dargestellt werden soll, sind verschiedene Diagramme sinnvoll.

Es sollen einzelne Werte abgelesen und verglichen werden: Säulendiagramm, Balkendiagramm
Es soll dargestellt werden, wie sich eine Größe (im Laufe der Zeit) verändert: Liniendiagramm.
Es soll dargestellt werden, wie groß Anteile an einem Ganzen sind: Kreisdiagramm, Streifendiagramm

Säulendiagramm

Balkendiagramm

Liniendiagramm

Streifendiagramm

Kreisdiagramm

Übung

Löse die Aufgaben aus dem Buch und vergleiche deine Lösungen mit denen hinten im Buch.

S. 134, P1 - P4
S. 135, P5 - P8
S. 136, P 9
S. 161, Nr. 1-3

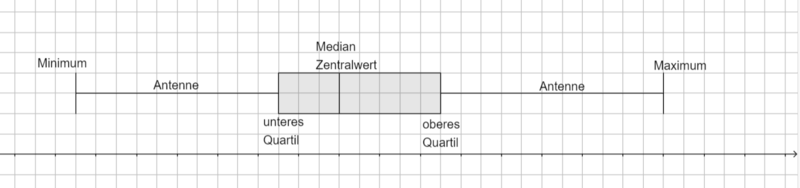
Statistische Kennwerte

Werden in einer statistischen Erhebung Daten gesammelt (z.B. die verschiedenen Körpergrößen in einer Klasse), werden diese mithilfe von Kennwerten ausgewertet. Die Daten werden zunächst in einer Urliste gesammelt. Ordnet man die Werte der Größe nach, so erhält man eine Rangliste.

Kennwerte
Kennwert	Bedeutung
Minimum	kleinster Wert
Maximum	größter Wert
Spannweite	Differenz aus Maximum und Minimum
Median/Zentralwert	Wert in der Mitte der Rangliste
unteres Quartil	Median der unteren Hälfte
oberes Quartil	Median der oberen Hälfte
Quartilabstand	Differenz aus oberem und unterem Quartil
Mittelwert (arithmetisches Mittel)	"Durchschnitt": Summe aller Werte geteilt durch Anzahl der Werte

Ordne die mathematischen Bezeichnungen und Formeln richtig zu.

arithmetisches Mittel	Durchschnitt	Mittelwert	$\bar{x}$	$\bar{m}$
Median	Zentralwert	$x_{Med}$	der mittlere Wert eines sortierten Urliste	Z
Modus	$x_{Mod}$	der häufigste Wert	Modalwert	m

Kennwerte - Beispiel Körpergrößen

Die Liste gibt die Körpergröße von 11 Personen an. Bestimme die statistischen Kennwerte und zeichne einen Boxplot.

Urliste (ungeordnet): 181cm; 159cm; 167cm; 170cm; 169cm; 184cm; 171cm; 177cm; 175cm; 177cm; 172cm

1. Schritt: Erstelle eine Rangliste: Ordne die Werte der Größe nach.

Rangliste: 159cm; 167cm; 169cm; 170cm; 171cm; 172cm; 175cm; 177cm; 177cm; 181cm; 188cm

2. Schritt: Ermittle die Kennwerte:

Minimum: 159cm
Maximum: 188cm
Spannweite: w = 188cm - 159cm = 29cm
Median/Zentralwert: Es gibt n=11 Werte, also befindet sich der Median auf dem 6. Rangplatz.
          (n:2 = 11:2 = 5,5; also 6. Rang)
          Auf dem 6. Rangplatz steht 172cm, also ist Z = 172cm
unteres Quartil: Median der unteren Hälfte, also befindet sich der Wert des unteren Quartils auf dem 3. Rangplatz.
          (n:4 = 11:4 = 2,75; also 3. Rang).
          Auf dem 3. Rangplatz steht 169cm, also ist q_u = 169cm
oberes Quartil: Median der oberen Hälfte, also befindet sich der Wert des unteren Quartils auf dem 3. Rangplatz.
          (n· $\tfrac{3}{4}$ = 11· $\tfrac{3}{4}$ = 8,25; also 9. Rang).
          Auf dem 9. Rangplatz steht 177cm, also ist q_u = 177cm
Quartilabstand: 177cm - 169cm = 8cm
Mittelwert: $\bar{m}$ = $\tfrac{159 + 167 + 169 + 170 + 171 + 172 + 175 + 177 + 177 + 181 + 188}{11}$ ≈ 173,3
Modus (Modalwert): m = 177cm (Dieser Wert kommt am häufigsten vor, nämlich zweimal.)

Boxplot:

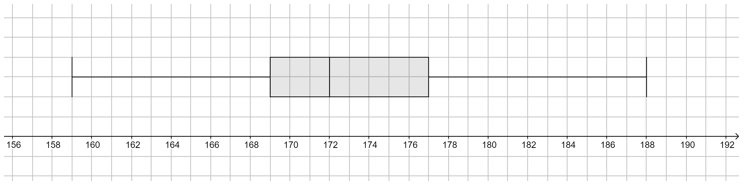
Boxplots

Boxplot

Die statistischen Kenngrößen Minimum, Maximum, Median und die Quartile können in einem Boxplot dargestellt werden.

Der Boxplot gibt einen Überblick, wie sich die Daten verteilen. Die Datenmenge wird Hälften bzw. Viertel eingeteilt:

50% der Daten liegen in der Box (zentrale Hälfte).
50% der Daten sind kleiner oder gleich groß wie der Median.
50% der Daten sind größer oder gleich groß wie der Median.
25% der Daten liegen zwischen dem Minimum und dem unteren Quartil, usw.
Die Spannweite entspricht der Breite des gesamten Boxplots.
Ist der Boxplot bzw. die Box sehr klein/eng, liegen die Daten dicht beieinander.

Übung

Löse die Aufgaben aus dem Buch. Vergleiche mit den angegebenen Lösungen.

S. 136, P10 und P11
S. 137, P12-P14
S. 162, Nr. 1-3

@@ Zeile 23: / Zeile 23: @@
 + 32%
-{In welchem Diagramm ist die Verteilung richtig dargestellt?
+{In welchem Diagramm ist die Verteilung der Beförderungsmittel richtig dargestellt (zu den Angaben oben)?
 [[Datei:Kreisdiagramme zu Schulwegen.png|rahmenlos]]}

	der Abstand zwischen Minimum und Maximum
	der Wert, der in der Datenreihe am häufigsten vorkommt
	die Summe aller Werte geteilt durch die Anzahl der Werte
	der mittlere Wert einer geordneten Rangliste

	arithmetisches Mittel $\bar{x}$ ≈ 19,10€
	arithmetisches Mittel $\bar{x}$ = 20,00€
	Zentralwert (Median) Z = 19,10€
	Zentralwert (Median) Z = 15,00€
	Spannweite w = 45,00€
	Spannweite w = 15,00€
	Modalwert m = 25,00€
	Modalwert m = 10,00€

	Die durchschnittlichen Handykosten für die 8-16 Jährigen betragen 7,50€.
	Die Hälfte aller 8-16 Jährigen gibt im Monat zwischen 5€ und 15€ für das Handy aus.
	Die Hälfte aller 17-25 Jährigen gibt im Monat mindestens 15€ aus.
	Das untere Quartil beträgt für die 17-25 Jährigen 10€.

Suche

Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik: Unterschied zwischen den Versionen

Version vom 11. März 2023, 12:29 Uhr

Inhaltsverzeichnis

Statistik

Einstiegstest: Diagramme, Statistik

Häufigkeiten

Diagramme

Statistische Kennwerte

Boxplots

Navigation

Projekte

ZUM

Hilfen

	8
	0,8
	8%
	32%

	Ja, das stimmt.
	Nein, das stimmt nicht.

Suche

Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Statistik: Unterschied zwischen den Versionen

Version vom 11. März 2023, 12:29 Uhr

Statistik

Einstiegstest: Diagramme, Statistik

Häufigkeiten

Diagramme

Statistische Kennwerte

Boxplots

Navigation

⧼timis-pagehighlighted⧽

⧼timis-pagenamespaces⧽

⧼timis-pagetranslate⧽

Seitenwerkzeuge

Seitenwerkzeuge