Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 243: | Zeile 243: | ||
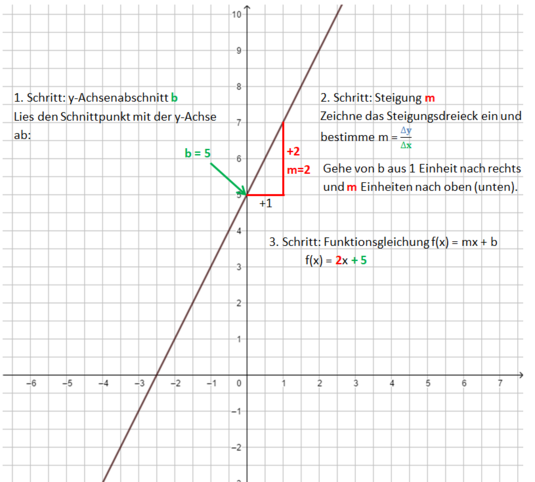
* Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.|Merksatz}} | * Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.|Merksatz}} | ||
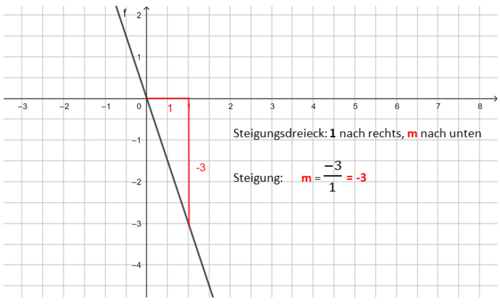
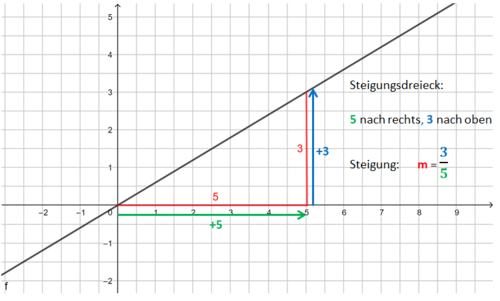
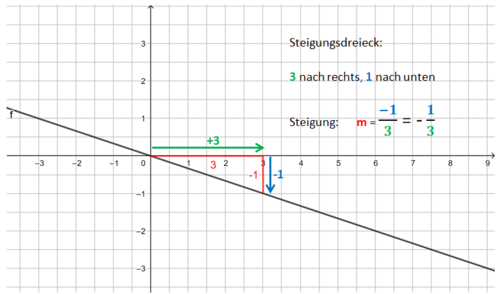
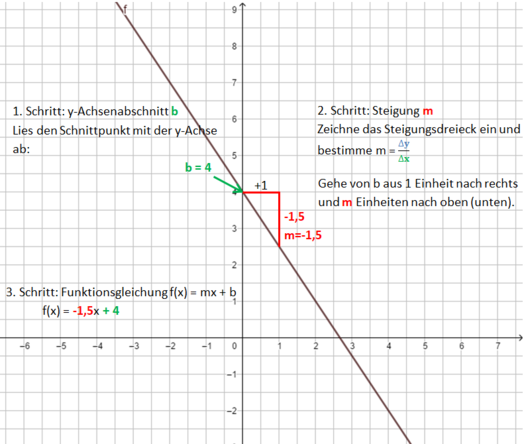
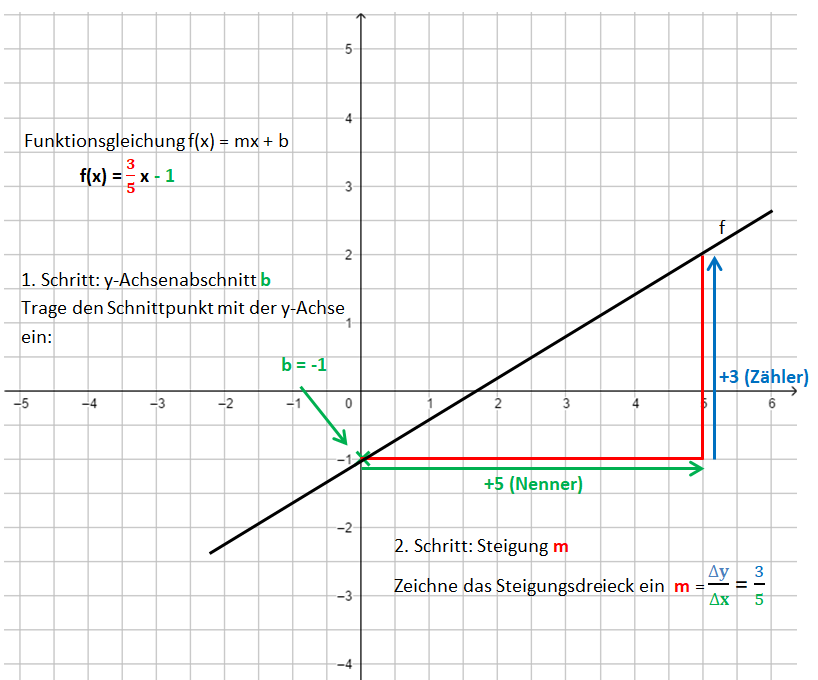
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = <math>{3 \over 5}</math>x - 1.<br> | Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = <math>{3 \over 5}</math>x - 1.<br> | ||
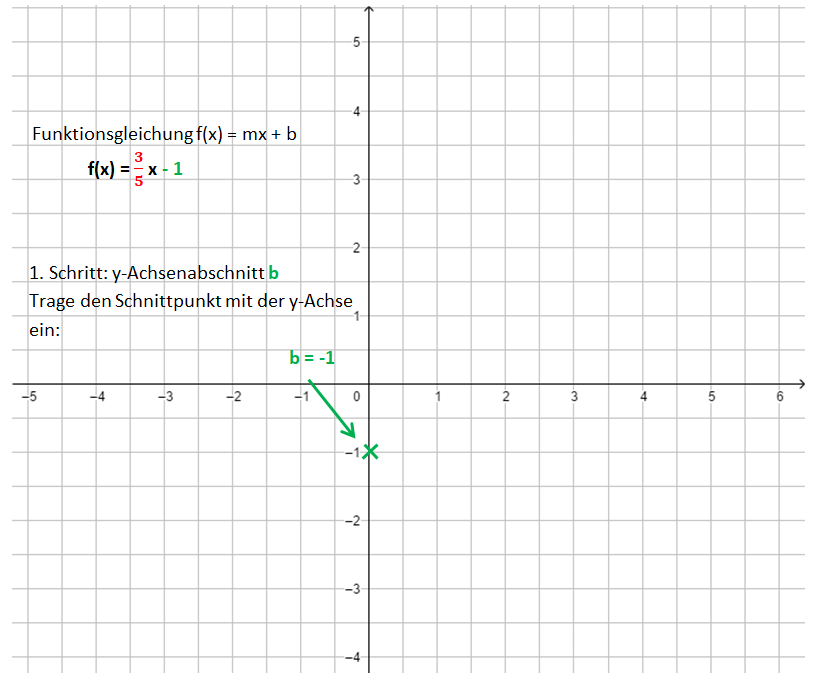
Schritt 1[[Datei:Gerade zur Gleichung zeichnen Schritt 1.png]] | Schritt 1[[Datei:Gerade zur Gleichung zeichnen Schritt 1.png]]<br> | ||
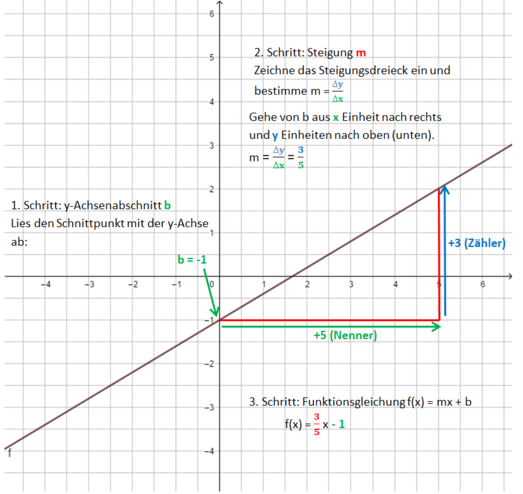
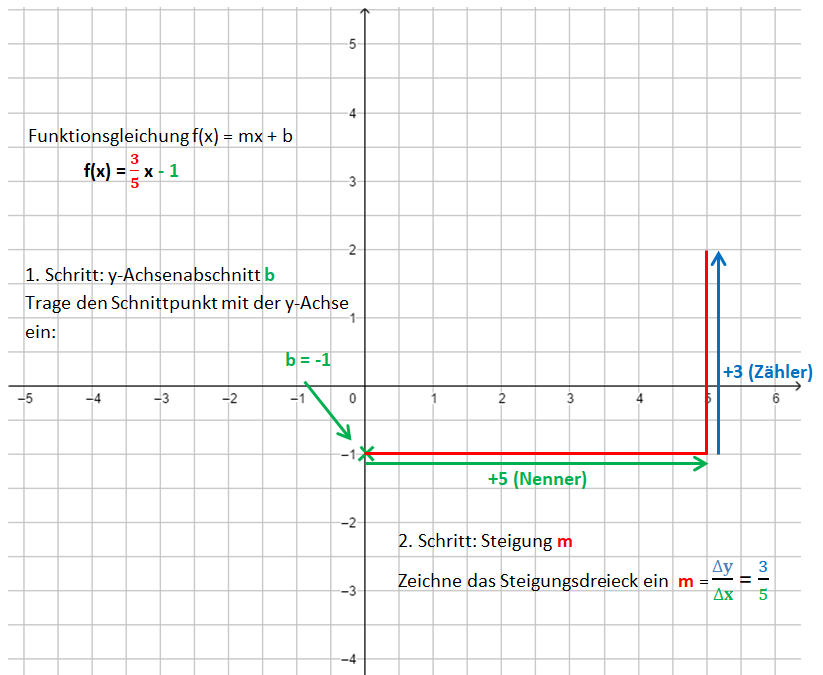
Schritt 2[[Datei:Gerade zur Gleichung zeichnen 2. Schritt.png]] | Schritt 2[[Datei:Gerade zur Gleichung zeichnen 2. Schritt.png]]<br> | ||
Schritt 3[[Datei:Gerade zur Gleichung zeichnen Schritt 3.png]] | Schritt 3[[Datei:Gerade zur Gleichung zeichnen Schritt 3.png]]<br> | ||
|- | |- | ||
!Video | !Video | ||
| Zeile 256: | Zeile 256: | ||
===Lineare Funktionen: Funktionsgleichung rechnerisch bestimmen=== | ===Lineare Funktionen: Funktionsgleichung rechnerisch bestimmen=== | ||
{{Box|Lineare Funktionen: Funktionsgleichung aufstellen mithilfe der Steigung und gegebener Punkte|Du kannst die Funktionsgleichung einer linearen Funktion auch rechnerisch bestimmen: | {|class=wikitable | ||
|- | |||
!Merksätze | |||
|{{Box|Lineare Funktionen: Funktionsgleichung aufstellen mithilfe der Steigung und gegebener Punkte|Du kannst die Funktionsgleichung einer linearen Funktion auch rechnerisch bestimmen: | |||
* Punkt-Steigungsform: die Steigung m und ein Punkt ist gegeben | * Punkt-Steigungsform: die Steigung m und ein Punkt ist gegeben | ||
* Zwei-Punkte-Form: zwei Punkte sind gegeben (hier findest du Informationen in der Formelsammlung)|Merksatz}} | * Zwei-Punkte-Form: zwei Punkte sind gegeben (hier findest du Informationen in der Formelsammlung)|Merksatz}} | ||
| Zeile 279: | Zeile 282: | ||
7 = b<br> | 7 = b<br> | ||
Also lautet die Funktionsgleichung f(x) = -2x + 7.<br> | Also lautet die Funktionsgleichung f(x) = -2x + 7.<br> | ||
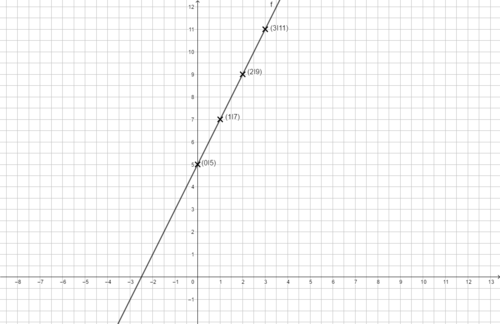
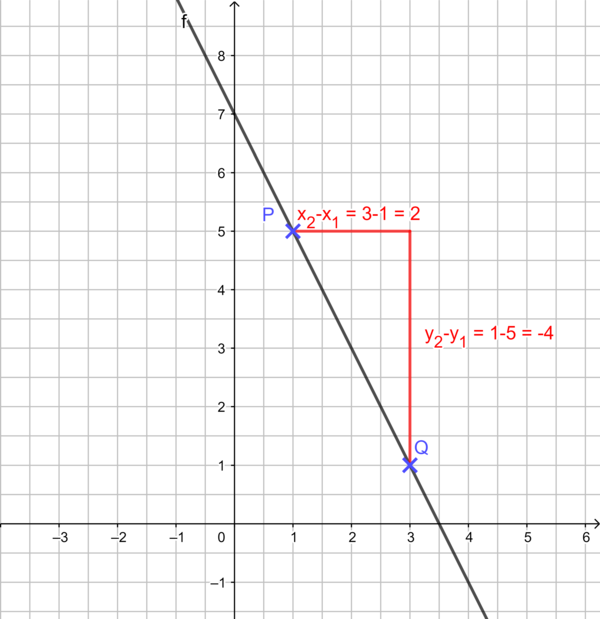
{{Lösung versteckt|1=Erkläre, wie du das Steigungsdreieck zwischen den Punkten P und Q einzeichnen kannst und wie du damit die Steigung m bestimmen kannst. | |{{Lösung versteckt|1=Erkläre, wie du das Steigungsdreieck zwischen den Punkten P und Q einzeichnen kannst und wie du damit die Steigung m bestimmen kannst. | ||
[[Datei:Zwei-Punkte-Form von f(x)=-2x+7.png|rahmenlos|619x619px]]|2=Bild zur Bestimmung von m (Funktionsgraph)|3=Verbergen}} | [[Datei:Zwei-Punkte-Form von f(x)=-2x+7.png|rahmenlos|619x619px]]|2=Bild zur Bestimmung von m (Funktionsgraph)|3=Verbergen}} | ||
|- | |||
{{#ev:youtube|bE-yJzIqeIU|500|left}}| | !Video | ||
|{{#ev:youtube|bE-yJzIqeIU|500|left}} | |||
|- | |||
!Übung | |||
| | |||
|} | |||
===Lineare Funktionen: Punktprobe=== | ===Lineare Funktionen: Punktprobe=== | ||
{{Box|1=Punktprobe|2=Wir können rechnerisch prüfen, ob ein Punkt auf dem Graphen der Funktion liegt. Dazu setzen wir die Koordinaten des Punktes P(<span style="color:red">x</span>I<span style="color:blue">y</span>) in die Funktionsgleichung <span style="color:blue">f(x)</span> = m<span style="color:red">x</span> + b ein. Der Punkt liegt auf dem Graphen, wenn sich eine wahre Aussage ergibt, die Gleichung also erfüllt ist.|3=Merksatz}} | {|class=wikitable | ||
{{LearningApp|app= ppkr9n4sj20|width= | |- | ||
!Merksätze | |||
|{{Box|1=Punktprobe|2=Wir können rechnerisch prüfen, ob ein Punkt auf dem Graphen der Funktion liegt. Dazu setzen wir die Koordinaten des Punktes P(<span style="color:red">x</span>I<span style="color:blue">y</span>) in die Funktionsgleichung <span style="color:blue">f(x)</span> = m<span style="color:red">x</span> + b ein. Der Punkt liegt auf dem Graphen, wenn sich eine wahre Aussage ergibt, die Gleichung also erfüllt ist.|3=Merksatz}} | |||
|- | |||
!Übung | |||
|{{LearningApp|app= ppkr9n4sj20|width=80%|height=400px}} | |||
|} | |||
===Lineare Funktionen: Nullstellen bestimmen=== | ===Lineare Funktionen: Nullstellen bestimmen=== | ||
{{Box|1=Schnittpunkte mit den Koordinatenachsen|2=Für den Schnittpunkt P<sub>y</sub> mit der y-Achse (y-Achsenabschnitt) setzen wir x = 0 in die Funktionsgleichung ein berechnen b. | {|class=wikitable | ||
|- | |||
P<sub>y</sub> (0|b) | !Merksätze | ||
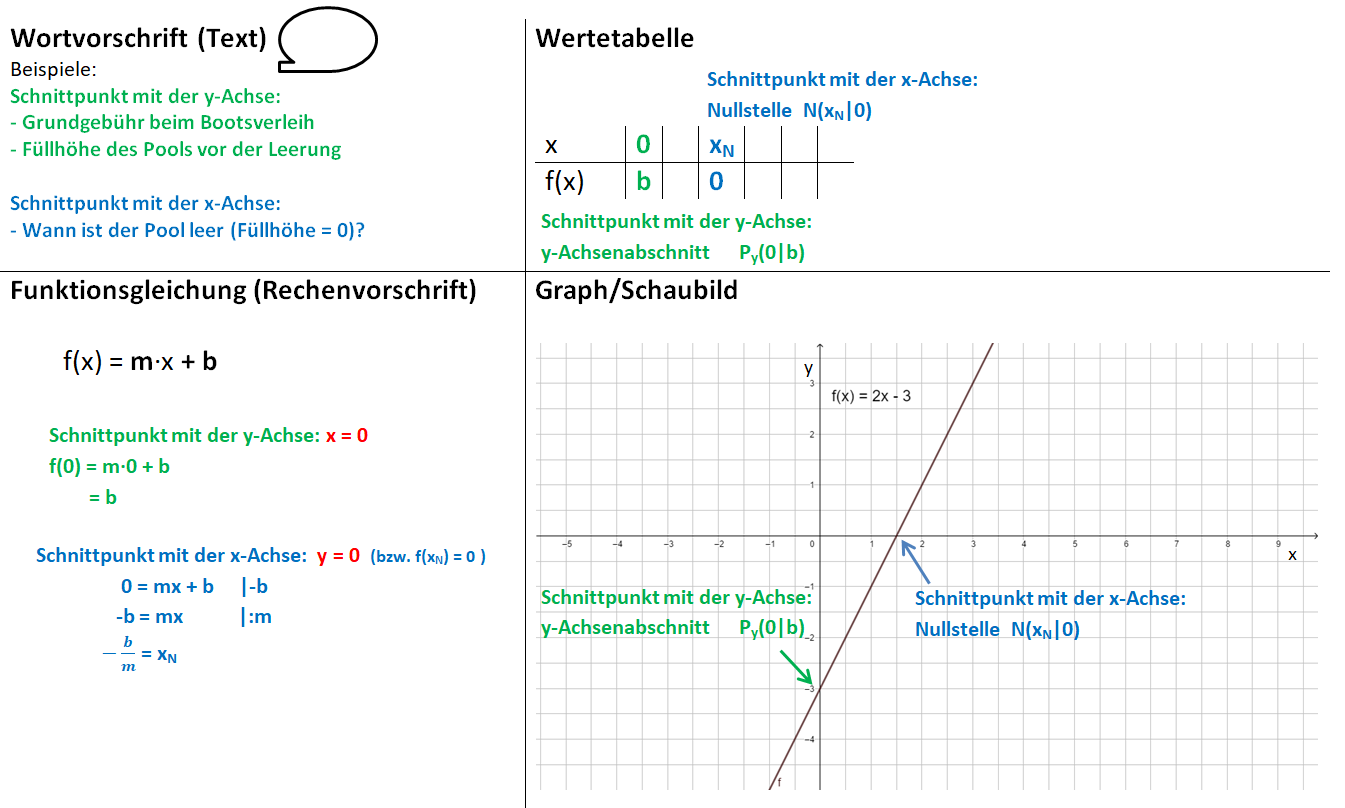
|{{Box|1=Schnittpunkte mit den Koordinatenachsen|2=Für den Schnittpunkt P<sub>y</sub> mit der y-Achse (y-Achsenabschnitt) setzen wir x = 0 in die Funktionsgleichung ein berechnen b. <br> | |||
P<sub>y</sub> (0|b)<br> | |||
Für den Schnittpunkt N mit der x-Achse (<b>Nullstelle</b>) setzen wir f(x) = 0 (oder y = 0) in die Funktionsgleichung ein und lösen die Gleichung nach x auf. | Für den Schnittpunkt N mit der x-Achse (<b>Nullstelle</b>) setzen wir f(x) = 0 (oder y = 0) in die Funktionsgleichung ein und lösen die Gleichung nach x auf. | ||
N (x<sub>N</sub>I0)|3=Merksatz}} | N (x<sub>N</sub>I0)|3=Merksatz}} | ||
[[Datei:Übersicht Schnittpunkte mit den Koordinatenachsen.png|Übersicht Schnittpunkte mit den Koordinatenachsen]] | [[Datei:Übersicht Schnittpunkte mit den Koordinatenachsen.png|Übersicht Schnittpunkte mit den Koordinatenachsen]] | ||
{{LearningApp|app=pu8028csj20|width= | |- | ||
!Übung | |||
|{{LearningApp|app=pu8028csj20|width=80%|height=400px}} | |||
{{Box|Übung|Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen mit denen hinten im Buch. | {{Box|Übung|Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen mit denen hinten im Buch. | ||
* S. 122, P2 - P9 | * S. 122, P2 - P9 | ||
* S. 150, Nr. 3-6|Üben}} | * S. 150, Nr. 3-6|Üben}} | ||
|} | |||
Version vom 21. Februar 2025, 17:25 Uhr
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag
Funktionen
Einstiegstest: Lineare Funktionen (hilfsmittelfreier Teil)
Lineare Funktionen erkennen
| Merksätze | |
|---|---|
| Video | |
| Übungen |
|
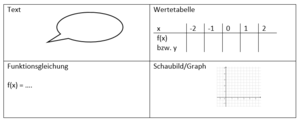
Lineare Funktionen: Wertetabelle
| Merksätze | |
|---|---|
| Video | |
| Übung |
|
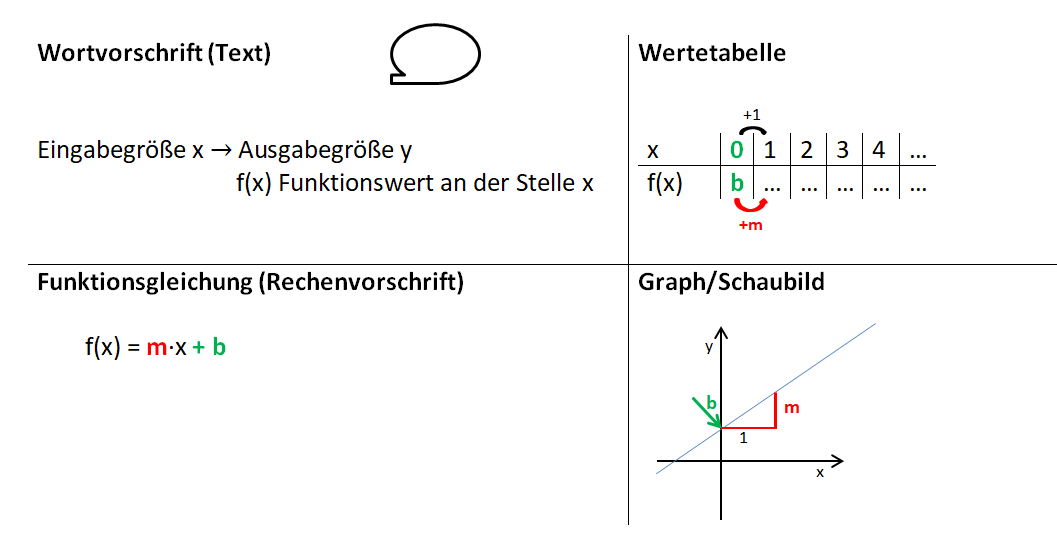
Lineare Funktionen: Gleichung und Graph
| Merksätze | |
|---|---|
| Übung |
|
| Merksätze |
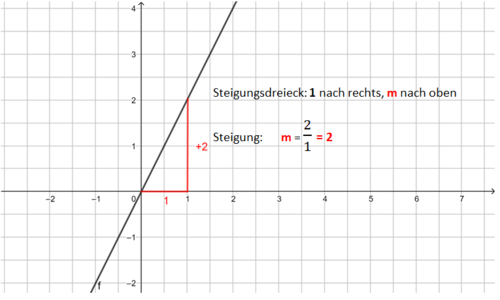
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1. |
|---|---|
| Video | |
| Übung | Übung realmath |
Lineare Funktionen: Funktionsgleichung rechnerisch bestimmen
| Merksätze |
Beispiel 1: Punkt-Steigungsform |
|
|---|---|---|
| Video | ||
| Übung |
Lineare Funktionen: Punktprobe
| Merksätze | |
|---|---|
| Übung |
|
Lineare Funktionen: Nullstellen bestimmen
| Merksätze | |
|---|---|
| Übung |
|