Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 121: | Zeile 121: | ||
===Lineare Funktionen erkennen=== | ===Lineare Funktionen erkennen=== | ||
{{Box|1=Lineare Funktionen erkennen|2=Eine Funktion, deren Funktionsgleichung die Form ''<b>f(x) = <span style="color:red>m</span>x + <span style="color:green">b</span></b>'' hat, heißt <b>lineare Funktion</b>. Der Graph einer linearen Funktion ist immer eine <b>Gerade</b> mit der <b><font color=red>Steigung m </font></b> und dem <b><font Color=green>y-Achsenabschnitt b</font></b>. Der Graph schneidet die y-Achse im Punkt P(0I<b><font Color=green>b</font></b>).<br> | {|class=wikitable | ||
|- | |||
!Merksätze | |||
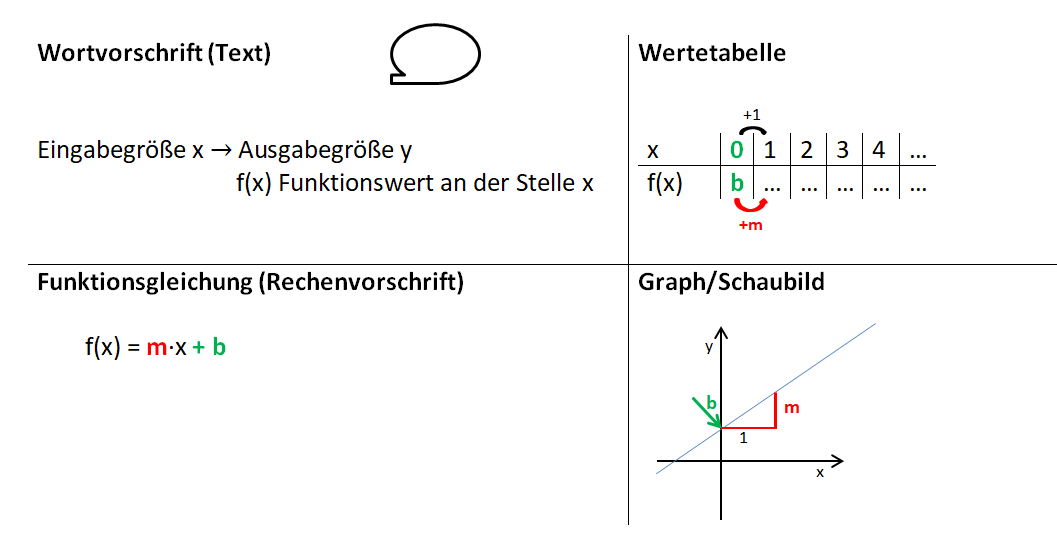
|{{Box|1=Lineare Funktionen erkennen|2=Eine Funktion, deren Funktionsgleichung die Form ''<b>f(x) = <span style="color:red>m</span>x + <span style="color:green">b</span></b>'' hat, heißt <b>lineare Funktion</b>. Der Graph einer linearen Funktion ist immer eine <b>Gerade</b> mit der <b><font color=red>Steigung m </font></b> und dem <b><font Color=green>y-Achsenabschnitt b</font></b>. Der Graph schneidet die y-Achse im Punkt P(0I<b><font Color=green>b</font></b>).<br> | |||
Lineare Funktionen erkennen:|3=Arbeitsmethode}} | Lineare Funktionen erkennen:|3=Arbeitsmethode}} | ||
[[Datei:Lineare Funktionen erkennen Zusammenfassung.png]] | [[Datei:Lineare Funktionen erkennen Zusammenfassung.png]] | ||
|- | |||
!Video | |||
|{{#ev:youtube|blY2qdFV4ag|800|left}} | |||
|- | |||
!Übungen | |||
{{#ev:youtube|blY2qdFV4ag|800| | |{{Box|Übung: Lineare Funktionen erkennen|Entscheide in den folgenden Apps, ob die Funktion linear ist oder nicht. In der letzten App gib die Funktionsgleichung an oder lies m und b ab.|Üben}} | ||
{{LearningApp|app=7222616|widtht=80%|height=400px}} | |||
{{Box|Übung: Lineare Funktionen erkennen|Entscheide in den folgenden Apps, ob die Funktion linear ist oder nicht. In der letzten App gib die Funktionsgleichung an oder lies m und b ab.|Üben}} | {{LearningApp|app=341227|width=80%|height=400px}} | ||
|} | |||
===Lineare Funktionen: Wertetabelle=== | ===Lineare Funktionen: Wertetabelle=== | ||
{{Box|1=Wertetabelle erstellen|2=Berechne den y-Wert der Funktion, indem du den x-Wert in die Funktionsgleichung einsetzt.<br> | {|class=wikitable | ||
|- | |||
!Merksätze | |||
|{{Box|1=Wertetabelle erstellen|2=Berechne den y-Wert der Funktion, indem du den x-Wert in die Funktionsgleichung einsetzt.<br> | |||
Beispiel Bootsverleih: y = 2x + 5<br> | Beispiel Bootsverleih: y = 2x + 5<br> | ||
Für x =<span style="color:red"> 1</span> gilt: y = 2 ·<span style="color:red"> 1</span> + 5<br> | Für x =<span style="color:red"> 1</span> gilt: y = 2 ·<span style="color:red"> 1</span> + 5<br> | ||
| Zeile 165: | Zeile 167: | ||
{{!)}} | {{!)}} | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
|- | |||
!Video | |||
|{{#ev:youtube|dLfPBJgHgC4|500|left}} | |||
|- | |||
!Übung | |||
|{{LearningApp|app=p46y09b6n19|width=80%|height=600px}} | |||
|} | |||
===Lineare Funktionen: Gleichung und Graph=== | ===Lineare Funktionen: Gleichung und Graph=== | ||
{{Box|Funktionsgraphen zeichnen|Trage die Punkte der Wertetabelle in ein Koordinatenkreuz ein und zeichne den Graphen der Funktion.<br> | {|class=wikitable | ||
|- | |||
!Merksätze | |||
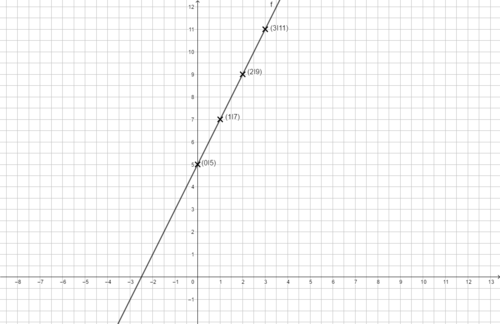
|{{Box|Funktionsgraphen zeichnen|Trage die Punkte der Wertetabelle in ein Koordinatenkreuz ein und zeichne den Graphen der Funktion.<br> | |||
Erinnerung:"Zuerst nach rechts und dann nach oben, dann werde ich dich loben" bzw. "Zuerst Anlauf nehmen, dann hoch springen."<br> | Erinnerung:"Zuerst nach rechts und dann nach oben, dann werde ich dich loben" bzw. "Zuerst Anlauf nehmen, dann hoch springen."<br> | ||
[[Datei:F(x)=2x+5 mit Punkten.png|rahmenlos|500x500px]] | [[Datei:F(x)=2x+5 mit Punkten.png|rahmenlos|500x500px]] | ||
|Kurzinfo}} | |Kurzinfo}} | ||
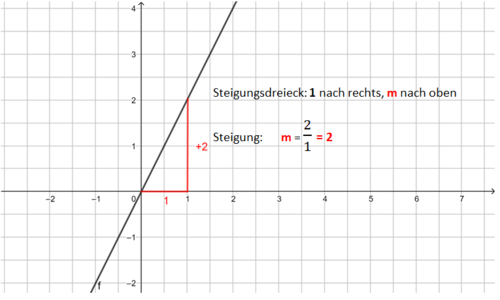
{{Box|Lineare Funktionen: Funktionsgleichung zu einer Geraden aufstellen|* Lies den y-Achsenabschnitt b ab. | {{Box|Lineare Funktionen: Funktionsgleichung zu einer Geraden aufstellen|* Lies den y-Achsenabschnitt b ab. | ||
* Zeichne das Steigungsdreieck und bestimme damit die Steiung m.|Merksatz}} | * Zeichne das Steigungsdreieck und bestimme damit die Steiung m.|Merksatz}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Beispiele:<br> | Beispiele:<br> | ||
| Zeile 194: | Zeile 204: | ||
</div> | </div> | ||
|2=Die Steigung mithilfe des Steigungsdreieckes bestimmen|3=Verbergen}} | |2=Die Steigung mithilfe des Steigungsdreieckes bestimmen|3=Verbergen}} | ||
|- | |||
!Video | |||
|{{#ev:youtube|XSqoULEHbe0|500|left}} | |||
|- | |||
!Übung | |||
| | |||
|} | |||
{|class=wikitable | |||
|- | |||
!Merksätze | |||
|Funktionsgleichungen vom Graphen ablesen<br> | |||
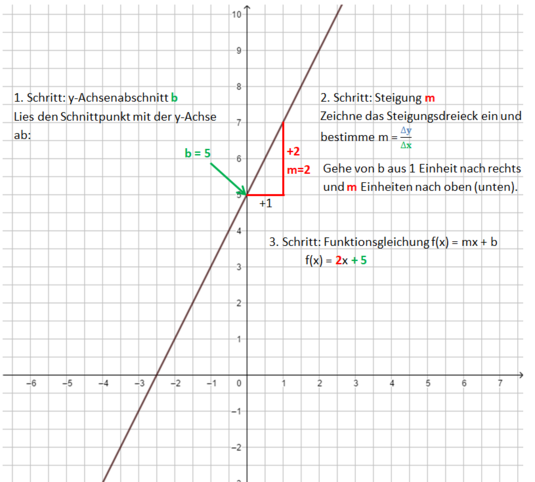
Beispiel 1 (leicht): m ist eine natürliche Zahl<br> | |||
[[Datei:Funktionsgleichung einer Geraden bestimmen m=2.png|535x535px]]<br> | |||
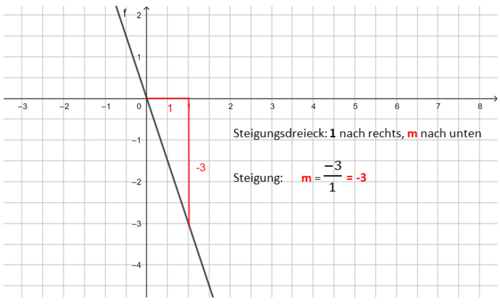
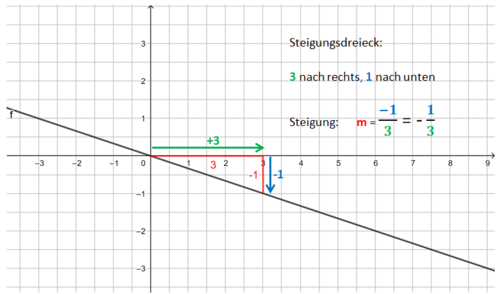
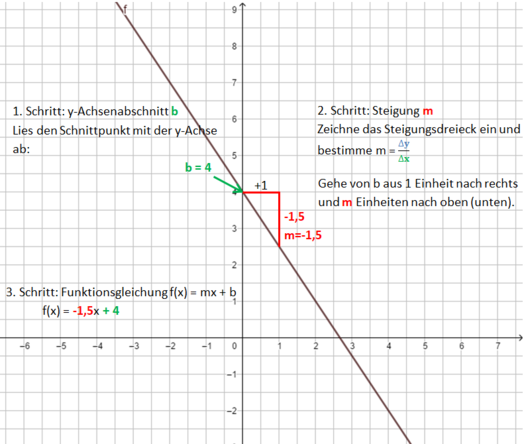
Beispiel 2 (mittel): m ist eine negative ganze Zahl <br> | |||
[[Datei:Funktionsgleichung einer Geraden bestimmen m=-1,5.png|528x528px]]<br> | |||
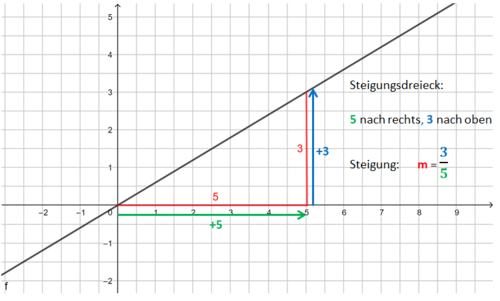
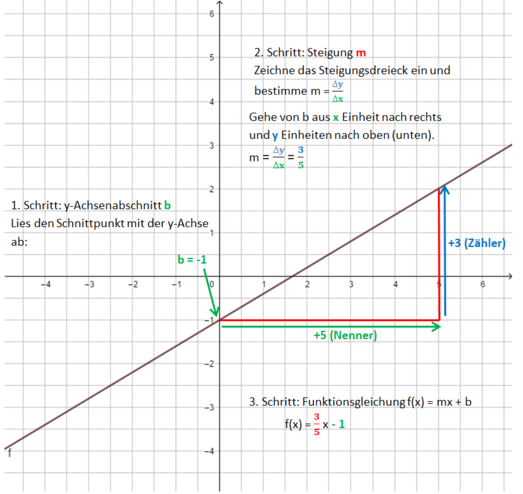
Beispiel 3 (schwer): m ist ein Bruch <br> | |||
[[Datei:Funktionsgleichung einer Geraden bestimmen m=drei Fünftel.png|523x523px]] | |||
|- | |||
!Video | |||
| | |||
|- | |||
!Übung | |||
|{{Box|Übung: Bestimmen der Funktionsgleichung einer Geraden|Ordne den Geraden die Funktionsgleichung zu. Wähle eine passende Schwierigkeit aus.|Üben}} | |||
leicht (*){{LearningApp|app=phd8q7we221|width=100%|height=400px}}{{LearningApp|app=p2rwidw3t20|width=100%|height=400px}} | |||
mittel (**){{LearningApp|app=popvxxk2v21|width=100%|height=400px}}{{LearningApp|app=pw8bbo2st20|width=100%|height=400px}} | |||
schwer (***){{LearningApp|app=p5mxjgbpt21|width=100%|height=400px}} | |||
{{LearningApp|app=ppn4q2oe320|width=100%|height=400px}} | |||
| | |||
|} | |||
{{LearningApp|app=ppn4q2oe320|width=100%|height=400px}} | |||
{{Box|Lineare Funktionen: Graph zeichnen|* Zeichne den y-Achsenabschnitt b ein. P(0|b) | {|class=wikitable | ||
|- | |||
!Merksätze | |||
|{{Box|Lineare Funktionen: Graph zeichnen|* Zeichne den y-Achsenabschnitt b ein. P(0|b) | |||
* Zeichne das Steigungsdreieck. Starte im Punkt P. Der Nenner gibt an, wie viele Einheiten du nach rechts gehst, der Zähler, wie viele Einheiten nach oben (unten). | * Zeichne das Steigungsdreieck. Starte im Punkt P. Der Nenner gibt an, wie viele Einheiten du nach rechts gehst, der Zähler, wie viele Einheiten nach oben (unten). | ||
* Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.|Merksatz}} | * Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.|Merksatz}} | ||
{{#ev:youtube|r6YopKFqk0c|800|center}} | {{#ev:youtube|r6YopKFqk0c|800|center}} | ||
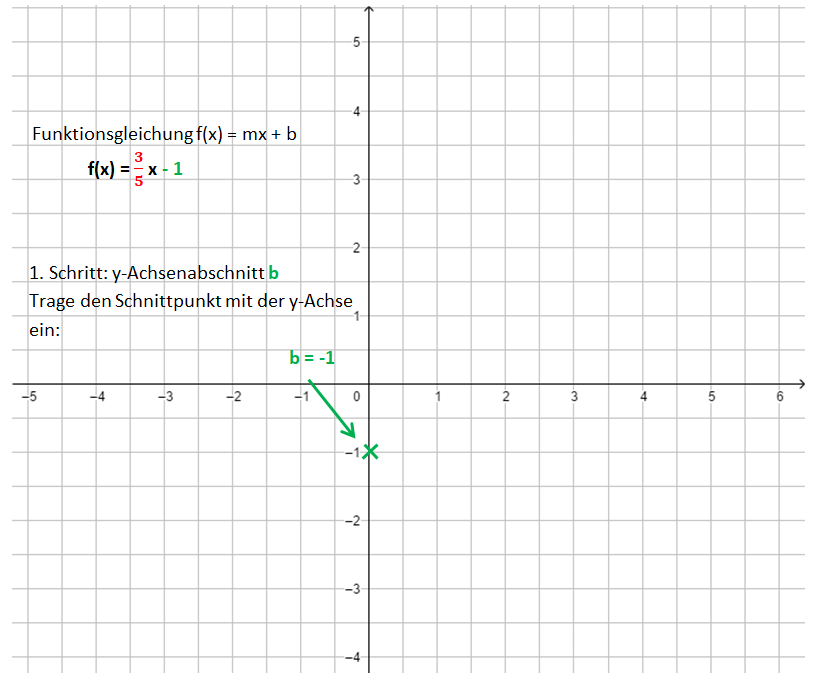
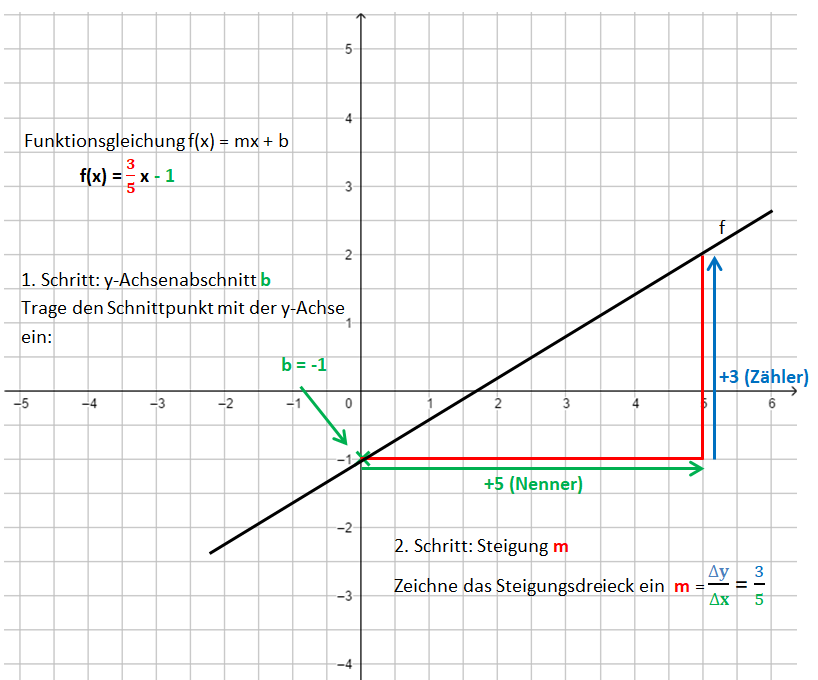
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = <math>{3 \over 5}</math>x - 1. | Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = <math>{3 \over 5}</math>x - 1. | ||
Schritt 1[[Datei:Gerade zur Gleichung zeichnen Schritt 1.png]] | |||
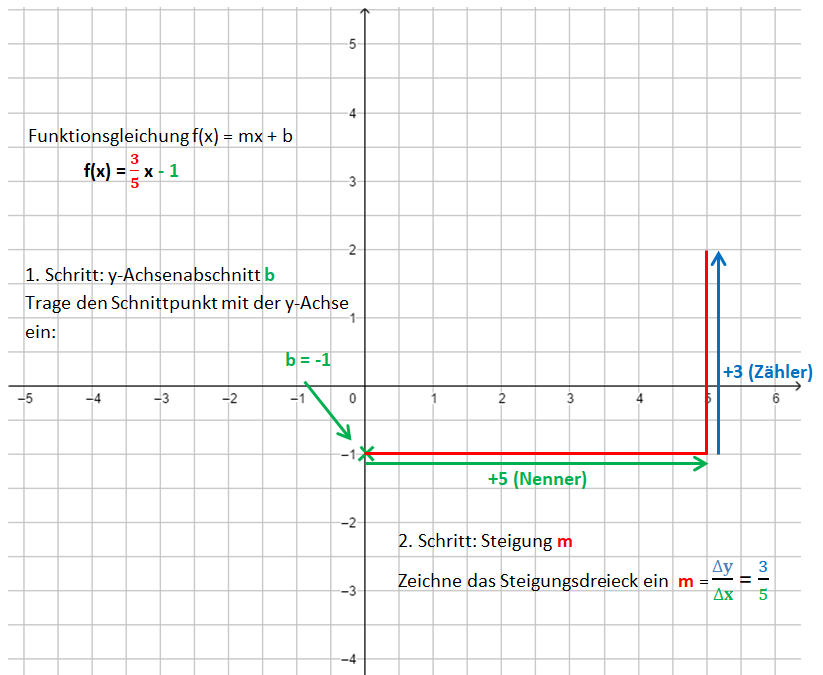
Schritt 2[[Datei:Gerade zur Gleichung zeichnen 2. Schritt.png]] | |||
Schritt 3[[Datei:Gerade zur Gleichung zeichnen Schritt 3.png]] | |||
|- | |||
!Video | |||
| | |||
|- | |||
!Übung | |||
| | |||
|} | |||
Version vom 21. Februar 2025, 17:05 Uhr
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag
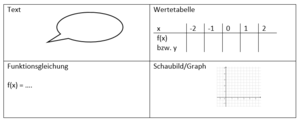
Funktionen
Einstiegstest: Lineare Funktionen (hilfsmittelfreier Teil)
Lineare Funktionen erkennen
| Merksätze | |
|---|---|
| Video | |
| Übungen |
|
Lineare Funktionen: Wertetabelle
| Merksätze | |
|---|---|
| Video | |
| Übung |
|
Lineare Funktionen: Gleichung und Graph
| Merksätze | |
|---|---|
| Video | |
| Übung |
| Merksätze |
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Schritt 1 |
|---|---|
| Video | |
| Übung |
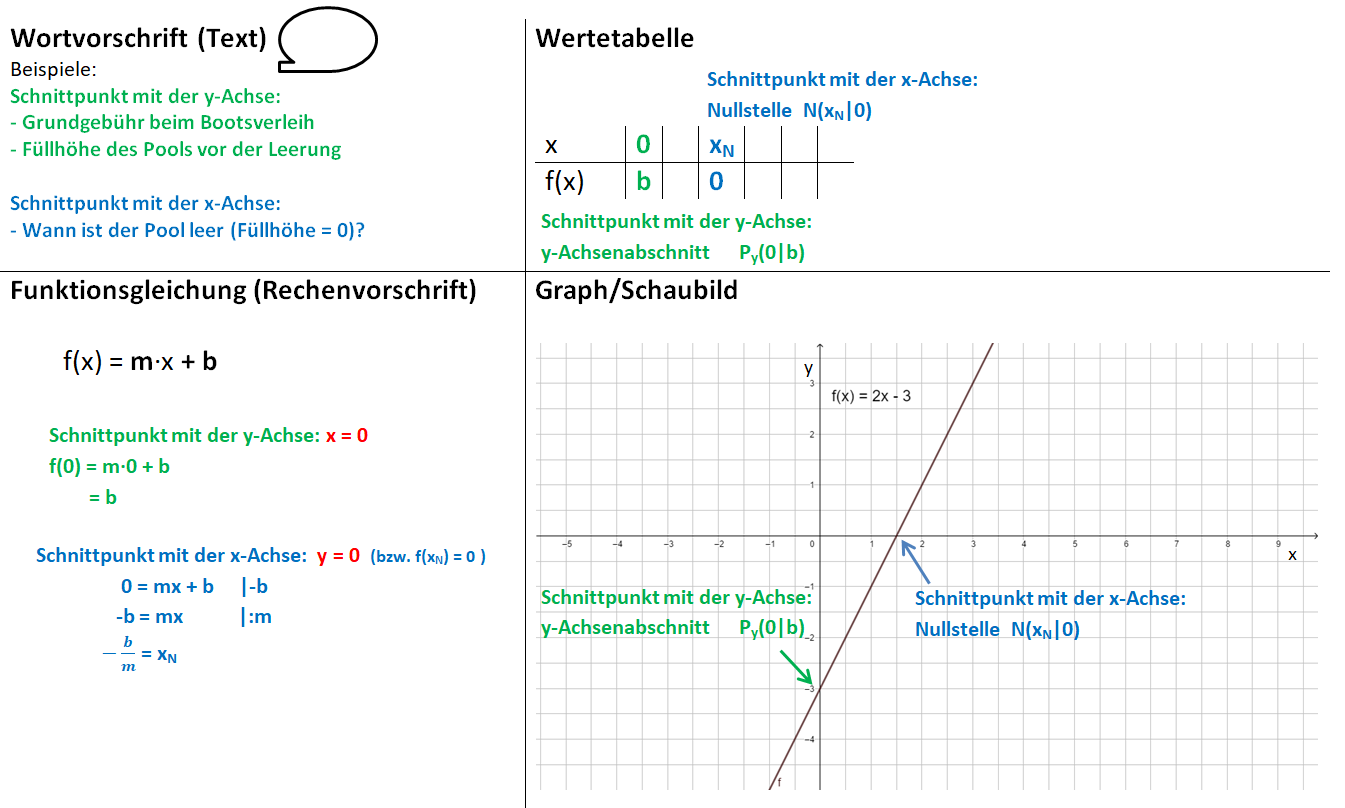
Lineare Funktionen: Funktionsgleichung rechnerisch bestimmen
Beispiel 1: Punkt-Steigungsform
geg: m = -1 und P(2|3)
ges: Funktionsgleichung der linearen Funktion
Idee: Setze m und die Koordinaten des Punktes in die Gleichung y = mx + b ein und bestimme so b.
f(x) = mx + b |m=-1 und P(2|3) einsetzen
3 = -1·2 + b |vereinfachen
3 = -2 + b |+2
5 = b
Also lautet die Funktionsgleichung f(x) = -1x + 5.
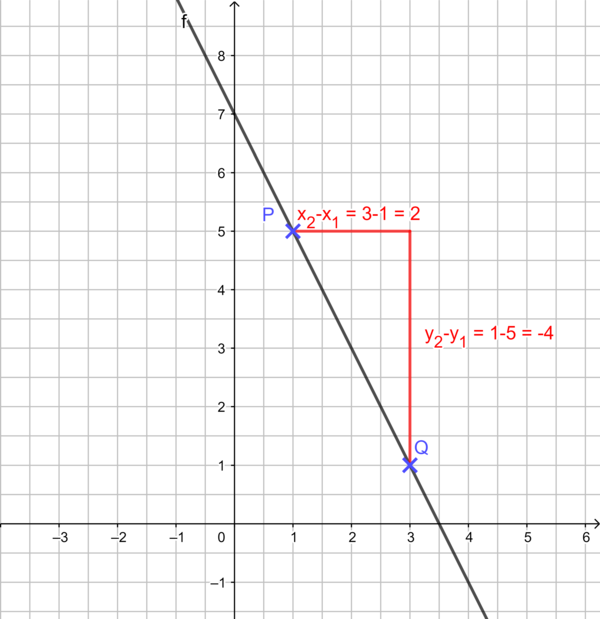
Beispiel 2: Zwei-Punkte-Form
geg: P(1|5) und Q(3|1)
ges: Funktionsgleichung der linearen Funktion
Bestimme die Steiung m: m = = = = -2
Bestimme b durch Einsetzen von m und einem der Punkte P oder Q in die Gleichung y = mx + b.
f(x) = mx + b |m=-2 und P(1|5) einsetzen
5 = -2·1 + b |vereinfachen
5 = -2 + b |+2
7 = b
Also lautet die Funktionsgleichung f(x) = -2x + 7.
Erkläre, wie du das Steigungsdreieck zwischen den Punkten P und Q einzeichnen kannst und wie du damit die Steigung m bestimmen kannst.
Lineare Funktionen: Punktprobe
Lineare Funktionen: Nullstellen bestimmen