Digitale Werkzeuge in der Schule/Mathematik im Beruf/Landschafts- und Gartenbauerinnen und -bauer

Info

In diesem Lernpfadkapitel widmen wir uns dem Beruf der Landschafts-/Gartenbauerin und des Landschafts-/Gartenbauers.

Für die Bearbeitung dieses Kapitels benötigst du dein Tablet, das zum Lernpfad gehörende Arbeitsblatt Landschafts- und Gartenbauerinnen und -bauer und einen Taschenrechner.

Bei den Aufgaben unterscheiden wir folgende Typen:

• Mit Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

Am Ende dieses Kapitels kannst du:

• benötigtes Material kalkulieren.
• einen Garten visualisieren.

Viel Erfolg!

Du wolltest immer schon erleben, wie die Arbeit als Landschafts- und Gartenbauerin oder -bauer aussieht?

Nun startet endlich deine Ausbildung bei einer Gartenbaufirma und du hilfst bei deinem ersten großen Auftrag: der Garten von Herrn Gründaumen soll neu aufbereitet werden! Bislang ist in dem Garten nur Wiese. Mit deinem Chef planst du eine Umzäunung, einen großen Teich und ein Hochbeet – die Elemente des Gartens, bei deren Planung und Bau Herr Gründaumen eure Unterstützung benötigt. Teilweise hat Herr Gründaumen konkrete Wünsche, die ihr bei eurer Arbeit natürlich bedenken möchtet.

Bei der Planung kommt eine wichtige Frage auf: Wie viel Material müsst ihr bestellen? Einige Materialien hat deine Gartenbaufirma schon vorrätig, andere noch nicht. Damit du deinem Chef die benötigten Mengen nennen kannst, bist du gerade dabei, alle Größen im Vorhinein zu berechnen. Dieser Lernpfad hilft dir dabei. Viel Erfolg!

Auf deinem Arbeitsblatt ist Platz für Notizen und eine Vorlage für die Materialliste. Nutze den Platz für Notizen, um dir wichtige Formeln und Rechenwege zu notieren. Wenn ein Ergebnis in die Materialliste eingetragen werden sollte, wirst du an der entsprechenden Stelle im Lernpfad darauf hingewiesen.

Teste dein Vorwissen

Bevor es losgeht, prüfe im folgenden Lückentext dein Wissen über Einheiten, Längen, Flächen und Volumina.

Aufgabe 1: Längen, Fläche, Volumina

Ordne die unteren Antwortmöglichkeiten jeweils einer Lücke zu und klicke anschließend auf "Prüfen!", um dir dein Ergebnis anzeigen zu lassen. Wenn die Antwortmöglichkeiten nach unten rutschen, bedeutet das, dass sie in eine andere Lücken gehören, probiere weiter!

Beim Rechnen mit Einheiten muss man immer darauf achten, dass diese übereinstimmen. Wenn dies nicht der Fall ist, müssen Einheiten umgerechnet werden. Dabei gilt $10$ dm = $1$ m = $100$ cm sowie $1$ $m^2$ = $100$ $\text{dm}^2$ = $10.000$ $\text{cm}^2$'. Die Formel, mit der man den Flächeninhalt eines Rechtecks berechnen kann, lautet: $A = a \cdot b$, wobei a und b die Seitenlängen des Rechtecks sind. Die Formel für eine Kreisfläche lautet $A = \pi \cdot r^2$ wobei r = $\frac {d}{2}$. Außerdem kann man das Volumen von verschiedenen Körpern berechnen, beispielsweise eines Quaders oder Zylinders. Das Volumen eines Quaders berechnet man mit der Formel $V = a \cdot b \cdot h$ und das Volumen eines Zylinders mit $V = \pi \cdot r^2 \cdot h$. Gut zu wissen ist auch, dass $1$ $\text{dm}^3$ = 1 Liter ergibt.

Nun geht es los mit der Planung des Gartens!

Aufgabenbereich 1: der Zaun

Info

Bei Aufgabe 2a) kannst du zwischen zwei Varianten wählen. Es reicht, wenn du eine der Varianten bearbeitest. Beachte, dass diese verschiedene Schwierigkeitsstufen haben.

Aufgabe 2a): Zaun

Herr Gründaumen wünscht sich einen Zaun, damit sein Hund im Garten frei laufen kann. Das Gartengrundstück ist rechteckig mit einer Länge von $20 \text{ m}$ und einer Breite von $35 \text{ m}$. Der Garten soll vollständig umzäunt werden. Von der Stadt wird vorgegeben, dass ein Gartenzaun in der Gegend, in der Herr Gründaumen wohnt, jeweils $2{,}5 \text{ m}$ innerhalb der Grundstücksgrenze liegen muss. Berechne die Länge des Zauns.

Da alle Seiten des Zauns $2{,}5 \text{ m}$ von der Grundstückkante entfernt liegen, ziehe an beiden Seiten diese Länge ab. Ein Rechteck hat die Eigenschaft, dass gegenüberliegende Seiten gleich lang sind, deswegen kannst du eine berechnete Seite mit 2 multiplizieren. So sieht also die Lösung aus: $U =(20 \text{ m} - 5 \text{ m}) \cdot 2 + (35 \text{ m} - 5 \text{ m}) \cdot 2 = 90 \text{ m}$

Aufgabe 2a): Zaun

Herr Gründaumen wünscht sich einen Zaun, damit sein Hund im Garten frei laufen kann. Das Gartengrundstück ist rechteckig mit einer Länge von $20 \text{ m}$ und einer Breite von $35 \text{ m}$. Der Garten soll vollständig umzäunt werden. Alle $5 \text{ m}$ und an jeder Ecke steht ein runder Pfeiler mit Radius $25 \text{ cm}$. Von der Stadt wird vorgegeben, dass ein Gartenzaun in der Gegend, in der Herr Gründaumen wohnt, jeweils $2{,}5 \text{ m}$ innerhalb Grundstücksgrenze liegen muss. Berechne die Länge des Zauns. Runde dein Ergebnis auf zwei Nachkommastellen.

Vielleicht hilft dir eine Zeichnung des Zauns, um ihn dir besser vorstellen zu können.

Der Kreisumfang U wird berechnet mit: $U = \pi \cdot r \cdot 2 = \pi \cdot d$. Dies kann bei der Berechnung der Pfeiler helfen.

Zunächst wird der Umfang ohne die Pfeiler berechnet: $(20 \text{ m} - 5 \text{ m}) \cdot 2 + (35 \text{ m} -5\text{ m}) \cdot 2 = 90 \text { m}$. Dann werden von diesem Umfang die Stellen, an denen ein Pfeiler steht abgezogen: $90 \text{ m} - (18 \cdot 0{,}5) = 81 \text{ m}$. Anschließend werden die Eckpfeiler addiert, hierbei ist zu beachten, dass nur $\frac{3}{4}$ des Pfeilers umrahmt werden muss: $81 \text{m} + 4 \cdot (\frac{3}{4}\pi \cdot 0{,}25 \text{ m} \cdot 2) = 85{,}71 \text{ m}$. Zum Schluss werden die 14 Pfeiler, welche an den Seiten stehen addiert, dabei ist zu beachten, dass nur $\frac{1}{2}$ des Pfeilers umrahmt werden muss: $85{,}71 + 14 \cdot (\frac{1}{2}\pi \cdot 0{,}25 \text{ m} \cdot 2) = 96{,}71 \text{ m}$. Somit ist der Zaun $96{,}71 \text{ m}$ lang.

Aufgabe 2b): Zaun

Auf einer Palette vom Baustoffhandel liegen immer $35 \text{ m}$ Zaun. Ermittle die Anzahl der Paletten für die in Aufgabe 2a) berechnete Länge des Zauns! Beachte, dass nur ganze Paletten im Handel erworben werden können.

Dein Chef muss 3 Paletten bestellen.

Wenn du die leichtere Aufgabe bearbeitet hast, berechne $90:35 = 2{,}57$ und runde auf ganze Paletten. Wenn du die schwierigere Aufgabe bearbeitet hast, berechne $96{,}71 : 35 = 2{,}76$ und runde auf ganze Paletten.

In beiden Fällen werden also 3 Paletten Zaun benötigt.

zurück zum Arbeitsblatt: Trage jetzt auf dem Arbeitsblatt ein, wie viele Paletten Zaun benötigt werden.

Aufgabenbereich 2: der Teich

Herr Gründaumen hat schon immer davon geträumt, einen großen runden Teich in seinem Garten zu haben. Dieser Teich wird wohl das größte Element im Garten. In eurer Planung nehmt ihr an, dass der Teich die Form eines Zylinders haben wird.

Aufgabe 3: Kreis und Zylinder

Wiederhole im Folgenden dein Wissen über Kreise und Zylinder, um den Teich danach gut planen zu können. Ziehe die Bilder in die jeweils richtige Hälfte und prüfe deine Zuordnung durch Klicken auf den Haken.

Damit kein Laub in diesen Teich reinfällt, möchte Herr Gründaumen außerdem einen Rollschutz aus PVC-beschichtetem Polyestergewebe über dem Teich anbringen lassen, den man selbst öffnen und schließen kann.

Aufgabe 4a): Maße des Teichs

Herr Gründaumens Wunsch nach einem kreisförmigen Teich. Dieser Wunsch soll mit einem Teich mit dem Durchmesser $60 \text{ dm}$ erfüllt werden. Für den Rollschutz werden in den Teich Pfeiler eingesetzt, an denen die Abdeckung befestigt wird und die mit dem Teichrand abschließen. Die Pfeiler werden mit einem Draht verbunden, dieser hat die Form des Teiches. Berechne die Länge des Drahtes, der um den Teich herum verlegt werden muss. Runde auf eine Nachkommastelle.

Die Formel zur Berechnung des Umfangs (=Länge des Drahtes) lautet $U = \pi \cdot 2 \cdot r = \pi \cdot d$.

Der Draht hat eine Länge von etwa $U = \pi \cdot 60 \text{ dm} = 188{,}5 \text{ dm}$.

zurück zum Arbeitsblatt: Trage jetzt auf dem Arbeitsblatt ein, wie viel Draht benötigt wird.

Info

Bei Aufgabe 4b) kannst du zwischen zwei Varianten wählen. Es reicht, wenn du eine der beiden Varianten bearbeitest. Beachte, dass diese verschiedene Schwierigkeitsstufen haben.

Aufgabe 4b): Maße des Teichs

Für seinen Teich, dessen Durchmesser $60 \text{ dm}$ beträgt, möchte Herr Gründaumen einen Rollschutz aus PVC-beschichtetem Polyestergewebe an den Pfeilern und dem Draht anbringen lassen. Dieser Rollschutz wird passgenau angefertigt und verdeckt exakt die Teichoberfläche. An den Seiten sind Seile befestigt, mit denen Herr Gründaumen den Rollschutz anbinden kann. Berechne die Fläche, die der Rollschutz abdecken muss. Runde dein Ergebnis auf zwei Nachkommastellen.

Nutze die Formel für eine Kreisfläche, um die Fläche des Teichs zu berechnen $A = \pi \cdot r^2$.

Die Wasseroberfläche des Teichs wird wie folgt ermittelt: $A = \pi \cdot 30^2 = 2.827{,}43 \text{ dm}^2$.

zurück zum Arbeitsblatt: Trage jetzt auf dem Arbeitsblatt ein, wie viel Rollschutz benötigt wird.

Aufgabe 4b): Maße des Teichs

Für seinen Teich, dessen Durchmesser $60 \text{ dm}$ beträgt, möchte Herr Gründaumen einen Rollschutz aus PVC-beschichtetem Polyestergewebe an den Pfeilern und dem Draht anbringen lassen. Dieser Rollschutz soll 110 % der Teichfläche bedecken und somit an den Seiten herausragen, sie wird an den Pfeilern befestigt. Berechne die Größe des Rollschutzes, die bestellt werden muss. Runde dein Ergebnis auf eine Nachkommastelle.

Nutze die Formel für eine Kreisfläche, um zuerst die Größe der Wasseroberfläche des Teichs zu berechnen $A = \pi \cdot r^2$.

Die Wasseroberfläche des Teiches wird mit folgender Formel ermittelt $A = \pi \cdot 30^2 = 2.827{,}43 \text{ dm}^2$. Anschließend berechnest du 10 % von $2.827{,}43 \text{ dm}^2$ wie folgt: $2.827{,}43 \text{ dm}^2 \cdot 0{,}1 = 282{,}74\text{ dm}^2$. Um nun die Größe der gesamten Abdeckung zu berechnen, addierst du beide Ergebnisse und rundest anschließend: $2.827{,}43 \text{ dm}^2 + 282{,}74\text{ dm}^2 = 3.110{,}2 \text{ dm}^2$.

ALTERNATIV:

$2.827{,}43 \text{ dm}^2 \cdot 1{,}1 = 3.110{,}2\text{ dm}^2$

zurück zum Arbeitsblatt: Trage jetzt auf dem Arbeitsblatt ein, wie viel Rollschutz benötigt wird.

Aufgabe 5: Wasserpumpe

Der kreisförmige Teich mit einem Durchmesser von $60 \text{ dm}$ aus Aufgabe 4 soll ein Fischteich werden. Da Fischteiche eine Wasserpumpe benötigen, die ungefähr zu der Wassermenge im Teich passt, ist nun zu berechnen, mit wie viel Wasser der Teich ungefähr gefüllt wird. Ihr könnt jedoch noch nicht genau absehen, wie tief der Teich im Endeffekt sein kann. Du nimmst an, dass der Teich die Form eines Zylinders haben wird und verschaffst dir einen Überblick über drei mögliche Tiefen.

Klicke die jeweils richtige Antwort an, prüfe sie durch Klicken auf den Haken und klicke dann auf den blauen Pfeil, um zur nächsten Aufgabe zu gelangen.

Die Formel zur Berechnung des Volumen lautet $V = \pi \cdot r^2 \cdot h$.

Wenn du das Volumen des Teichs berechnet hast, beachte: $1 \text{ dm}^3 = 1 \text{ l}$.

Die verschiedenen Volumina kannst du wie folgt berechnen:

$V= \pi \cdot (30\text{ dm})^2 \cdot 5\text{ dm} = 14.137{,}17 \text{ dm}^3 \text{ und } 14.137{,}17 \text{ dm}^3 = 14.137{,}17 \text{ l}$ oder $V= \pi \cdot (30\text{ dm})^2 \cdot 8\text{ dm} = 22.619{,}47 \text{ dm}^3 \text{ und } 22.619{,}47 \text{ dm}^3 = 22.619{,}47 \text{ l}$ oder

$V= \pi \cdot (30\text{ dm})^2 \cdot 11\text{ dm} = 31.101{,}77 \text{ dm}^3 \text{ und } 31.101{,}77 \text{ dm}^3 = 31.101{,}77 \text{ l}$

zurück zum Arbeitsblatt: Trage jetzt auf dem Arbeitsblatt ein, für welche Wassermengen eine Wasserpumpe benötigt werden könnte.

Sehr gut! Alle weiteren benötigten Materialien, wie zum Beispiel Folie zum Auskleiden des Teichs, hat deine Gartenbaufirma noch vorrätig. Das wird ein großes Projekt, schließlich werdet ihr das gesamte Volumen des Teichs selber ausheben!

Aufgabenbereich 3: das Hochbeet

In einem schönen Garten darf ein Hochbeet nicht fehlen, findet Herr Gründaumen. Wusstest du, dass ein Hochbeet aus mehreren Schichten besteht? Im folgenden Applet erfährst du, wie ein Hochbeet aufgebaut sein kann, damit du danach das Hochbeet für Herrn Gründaumen planen kannst.

Aufgabe 6: Aufbau eines Hochbeets

Klicke auf die blauen Stecknadeln in der Abbildung und wähle die Bezeichnung der jeweiligen Schicht. Wenn du fertig bist, prüfe dein Ergebnis durch einen Klick auf den Haken.

Einen Großteil der benötigten Materialien hat deine Gartenbaufirma schon vorrätig, lediglich Holz und Erde aktuell nicht. Daher berechnest du im Folgenden, wie viel Holz und Erde benötigt wird.

Aufgabe 7a): Material für das Hochbeet

Herr Gründaumen wünscht sich ein Hochbeet, das die Form eines Quaders hat und hüfthoch ist, damit er gut im Stehen daran arbeiten kann. Du hast gehört, dass vorgeschnittene Holzbretter der Längen $2{,}1 \text{ m}$ und $1{,}25 \text{ m}$ im lokalen Großhandel für Gartenbaubedarf aktuell übrig sind und günstig erworben werden können. Daher planst du ein Hochbeet, das $2{,}1 \text{ m}$ lang und $1{,}25 \text{ m}$ breit ist. Berechne die Menge an Holz in Quadratmetern, die für die Seiten und den Boden des Hochbeets benötigt werden.

Überlege dir, wie hoch "hüfthoch" ist.

Eine Standardhöhe für Hochbeete ist $1 \text{ m}$. Die meisten Hochbeete sind zwischen $0{,}8 \text{ m}$ und $1{,}1 \text{ m}$ hoch.

Du musst die Flächen für die Seiten einzeln berechnen und dann addieren.

Beispiellösungsweg für eine Höhe von $1 \text{ m}$: $2 \cdot (2{,}1 \text{ m} \cdot 1 \text{ m}) + 2\cdot (1{,}25 \text{ m} \cdot 1 \text{ m})+(2{,}1 \text{ m} \cdot 1{,}25 \text{ m}) = 9{,}33 \text{ m}^2$.

Insgesamt brauchst du also $9{,}33 \text{ m}^2$ Holz.

zurück zum Arbeitsblatt: Trage jetzt auf dem Arbeitsblatt ein, wie viel Holz benötigt wird.

Aufgabe 7b): Material für das Hochbeet

Wie du oben siehst, besteht die oberste Schicht eines Hochbeets aus Erde. Überlege dir (mit Hilfe der Abbildung aus Aufgabe 6 und der Höhe des Hochbeets aus Aufgabe 7a), wie hoch die oberste Schicht aus Erde sein könnte, und berechne die benötigte Menge an Erde.

In den meisten Hochbeeten ist die oberste Schicht aus Erde zwischen $20 \text{ cm}$ und $45 \text{ cm}$ hoch.

$\text{Volumen} = \text{Länge} \cdot \text{Höhe} \cdot \text{Breite}$

Hier ein beispielhafter Lösungsweg, um die benötigte Menge an Erde bei einer Höhe von $30 \text{ cm}$ zu berechnen: $2{,}1 \text{ m} \cdot 1{,}25 \text{ m} \cdot 0{,}3 \text{ m} = 0{,}79 \text{ m}^3$

zurück zum Arbeitsblatt: Trage jetzt auf dem Arbeitsblatt ein, wie viel Erde benötigt wird.

Abschluss: der Garten

Zum Abschluss steht noch eine kreative Aufgabe an:

Aufgabe 8: Zeichnung des Gartens

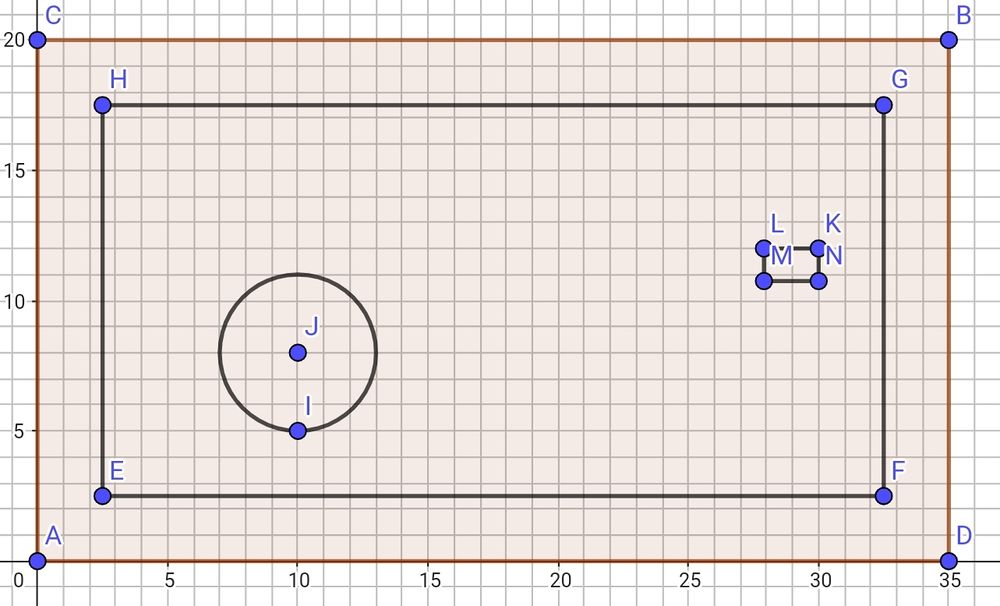
Dein Chef möchte unter deiner Materialliste eine maßstabsgetreue Zeichnung des Gartens haben. Versuche, mit Hilfe von GeoGebra eine Zeichnung des Gartens zu erstellen. Du darfst frei entscheiden, wie du die einzelnen Objekte platzierst. Lasse deiner Kreativität freien Lauf!

zurück zum Arbeitsblatt: Wenn du fertig bist, mache einen Screenshot deiner Skizze und füge ihn auf dem Arbeitsblatt ein.

Nun kannst du deinem Chef die fertige Materialliste mit der Zeichnung des Gartens geben. Gute Arbeit – er ist wirklich zufrieden!

zurück zur Kapitelauswahl