Digitale Werkzeuge in der Schule/Fit für VERA-8/Volumen und Oberfläche des Prismas

Info

In diesem Lernpfadkapitel beschäftigst du dich mit Prismen. Du lernst, das Prisma von anderen geometrischen Körpern abzugrenzen sowie die Oberfläche und das Volumen eines Prismas zu berechnen.

Dazu haben wir für dich Aufgaben in verschiedenen Schwierigkeitsstufen:

• Mit Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit
• und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Wir wünschen dir viel Erfolg!

Das Prisma

Definition

Ein Prisma ist ein Körper, der durch zwei zueinander parallele und deckungsgleiche Vielecke sowie durch Rechtecke begrenzt wird.

Die beiden zueinander parallelen und deckungsgleichen Vielecke heißen Grundflächen und die Rechtecke Seitenflächen.

Alle Seitenflächen bilden zusammen die Mantelfläche des Prismas und als Höhe des Prismas wird der Abstand der Grundflächen voneinander bezeichnet.

Vier Prismen mit unterschiedlichen, orange eingefärbten Grundflächen. Die Höhe der Prismen entspricht der Länge der schwarzen Linien.

Prismen und andere Körper

Aufgabe 1: Prismen erkennen

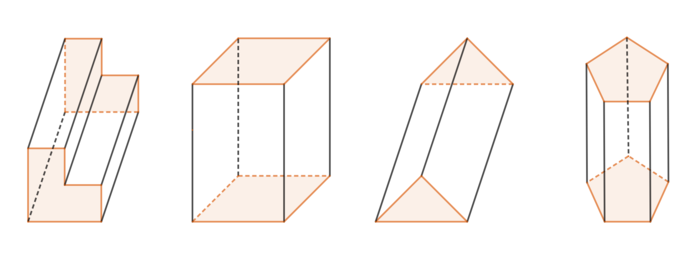
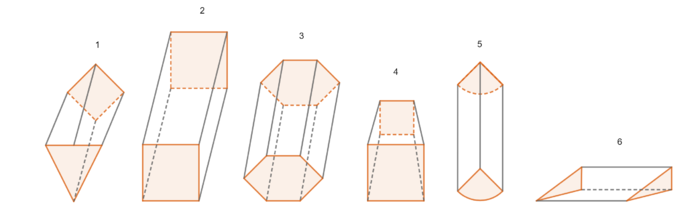
Welche der angegeben Körper sind Prismen? Ordne die Körper richtig zu, indem du sie in die entsprechenden Felder bewegst. Klicke abschließend auf den Haken im blauen Kästchen, um deine Zuordnung zu überprüfen.

• Körper 1 ist kein Prisma, da die Grundflächen verschiedene Vielecke sind, die somit nicht deckungsgleich sein können.
• Körper 2 ist ein Prisma mit quadratischen Grundflächen. Körper 2 ist zudem ein Quader.
• Körper 3 ist ein Prisma mit sechseckigen Grundflächen.
• Körper 4 ist kein Prisma, da die Grundflächen unterschiedlich groß und somit nicht deckungsgleich sind.
• Körper 5 ist kein Prisma, da die Grundflächen keine Vielecke, sondern Kreisschnitte sind.
• Körper 6 ist ein Prisma mit rechtwinkligen Dreiecken als Grundflächen.

Aufgabe 2: Netze

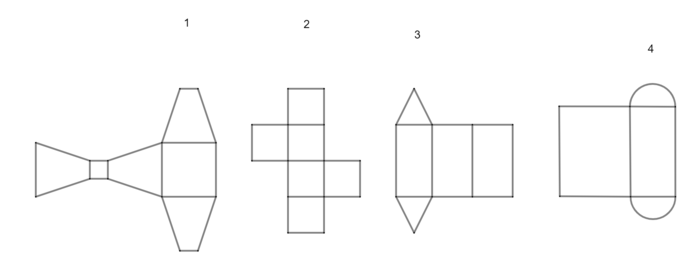
Welches dieser Körpernetze kann man zu einem Prisma zusammensetzen? Ordne die Netze richtig zu, indem du sie in die entsprechenden Felder bewegst. Klicke abschließend auf den Haken im blauen Kästchen, um deine Zuordnung zu überprüfen. Solltest du nicht mehr wissen, was das Netz eines Körpers ist oder wie du es zeichnest, guck doch einmal hier nach.

• Netz 1 kann zu einer Pyramide mit abgeflachter Spitze, aber nicht zu einem Prisma zusammengesetzt werden.
• Netz 2 kann zu einem Würfel und damit zu einem Prisma zusammengesetzt werden.
• Netz 3 kann zu einem Prisma mit dreieckigen Grundflächen zusammengesetzt werden.
• Netz 4 kann zu einem Zylinderschnitt, aber nicht zu einem Prisma zusammengesetzt werden.

Aufgabe 3: Körpernetz zeichnen

Zeichne das Netz eines Prismas mit folgenden Eigenschaften:

• Die Grundflächen sind Rechtecke, bei denen die langen Seiten doppelt so lang sind wie die kurzen.
• Das Prisma ist dreimal so hoch wie die langen Seite der Grundflächen lang sind.

• Zeichne zunächst eine der Grundflächen ein.
• Überlege, wie viele Seitenflächen das Prisma hat.

Dein gezeichnetes Netz könnte etwa so aussehen:

Beachte, dass es sehr viele Möglichkeiten gibt, ein Körpernetz zu zeichnen. Dadurch, dass die Längenverhältnisse, nicht aber die Längen der kurzen oder langen Seiten der Grundflächen vorgegeben sind, kann das Netz des Prismas unterschiedlich groß werden.

Veranschaulichung

Bewege den Regler "n", um die Grundflächen des Prismas zu verändern und den Regler "Öffnen", um zwischen Prisma und Körpernetz zu wechseln. Überlege dir, wie die Anzahl der Seitenflächen mit der Grundfläche zusammenhängt.

Die Anzahl der Seitenflächen des Prismas stimmt mit der Anzahl der Ecken der Grundfläche überein.

Aufgabe 4: Zusammenfassung

Vielleicht sind dir bei den bisherigen Aufgaben schon Besonderheiten des Prismas und Unterschiede oder Gemeinsamkeiten zu anderen Körpern aufgefallen. Um dein Wissen zu vertiefen und das Erlernte zu festigen, fülle den folgenden Lückentext aus, indem du die korrekten Wörter in die jeweiligen Lücken ziehst.

Das Prisma besteht aus zwei Grundflächen, die deckungsgleich und parallel zueinander liegen. Der Abstand der Grundflächen zueinander wird als Höhe des Prismas bezeichnet. Miteinander verbunden werden die Grundflächen durch Rechtecke, die Seitenflächen genannt werden. Addierst du die Flächeninhalte aller Seitenflächen, erhältst du die Mantelfläche des Prismas. Im Vergleich mit anderen geometrischen Körpern fällt auf, dass alle Quader und Würfel Prismen sind, aber nicht jedes Prisma ein Quader oder Würfel ist. Und im Gegensatz zum Zylinder, der runde Grundflächen hat, sind die Grundflächen des Prismas eckig.

Vor dem Rechnen: Verständnis, Größen und Einheiten

Aufgabe 5: Verständnis und Wiederholung

Das Arbeiten mit den Dimensionen Breite, Länge und Höhe kann manchmal ganz schön kompliziert sein. Wann nutzt man Addition, wann Multiplikation? Warum haben einige Einheiten Exponenten (Hochzahlen)? Beantworte die folgenden Fragen, indem du auf das richtige Kästchen klickst! Hast du alle Fragen beantwortet, klicke auf "Prüfen".

Gegeben sei die Breite eines Rechtecks. Du willst einen Flächeninhalt berechnen! Was musst du tun? (!Die Breite mit der Länge des Rechtecks addieren) (Die Breite mit der Länge des Rechtecks multiplizieren) (!Die Breite mit dem Grundflächeninhalt eines Prismas addieren) (!Die Breite mit dem Grundflächeninhalt eines Prismas multiplizieren)

Gegeben sei die Breite eines Quaders. Du möchtest ein Volumen berechnen! Was musst du tun? (!Die Breite mit der Länge und der Höhe des Quaders jeweils addieren) (Die Breite mit der Länge und der Höhe des Quaders jeweils multiplizieren) (!Die Breite mit dem Flächeninhalt einer Seitenfläche und einer Grundfläche des Quaders jeweils addieren) (!Die Breite mit dem Flächeninhalt einer Seitenfläche und einer Grundfläche des Quaders jeweils multiplizieren)

Gegeben sei eine Seitenfläche aus Länge und Höhe eines Quaders. Du möchtest ein Volumen berechnen! Was musst du tun? (!Die Breite mit dem Seitenflächeninhalt addieren) (Die Breite mit dem Seitenflächeninhalt multiplizieren) (!Die Flächeninhalte der Seitenfläche mit einer Grundfläche addieren) (!Die Flächeninhalte der Seitenflächen mit einer Grundfläche multiplizieren)

Gegeben seien unterschiedliche Seitenlängen, Flächeninhalte und Volumen! Ergeben sich sinnvolle Ergebnisse, wenn man zwei beliebige Größen miteinander addiert? (!Ja, ohne Einschränkungen) (!Um sinnvoll zu sein, müssen alle Einheiten unbedingt völlig gleich sein, z.B. cm mit m ergibt nichts Sinnvolles, dafür dm mit dm usw.) (!Um sinnvoll zu sein, müssen alle Einheiten gleich sein, aber der Exponent darf anders sein, z.B. cm mit m² ergibt nichts Sinnvolles, dafür dm² mit dm³ usw.) (Sinnvoll addieren kann man nur Seitenlängen mit Seitenlängen, Flächeninhalte mit Flächeninhalten oder Volumen mit Volumen) (!Nein, niemals)

Die Exponenten bei den Einheiten ... (!dienen nur der besseren Unterscheidung) (!erhöhen sich mit der gleichen Anzahl an Additionen, maximal drei Additionen) (erhöhen sich mit der gleichen Anzahl an Multiplikationen, maximal drei Multiplikationen) (!sind willkürlich)

Die Einheiten der Länge, z.B. cm oder m, stehen ohne Exponent, weil ... (!dort kein Exponent existiert) (!der Exponent eigentlich 0 ist und eine Null kann fast immer weggelassen werden) (der Exponent eigentlich 1 ist und man eine einfachere Schreibweise bevorzugt)

Aufgabe 6: Ordnen

Längen, Flächen und Volumen haben jeweils eigene Einheiten. Ordne die angegeben Einheiten richtig zu! Wenn du fertig und zufrieden bist, klicke unten rechts auf den blauen Haken.

Oberfläche eines Prismas

Hinweis

In diesem Abschnitt beschäftigst du dich mit den unterschiedlichen Flächen des Prismas. Die Oberfläche eines Prismas ergibt sich aus den vielen Seitenflächen, auch Mantelfläche genannt, zusammen mit den beiden Grundflächen. Fügst du diese zu einem Körper zusammen, wird umgangssprachlich auch von einem Hohlkörper gesprochen.

Erinnerung

Falls du einige der Grundlagen nicht mehr weißt, kannst du die Formeln hier nochmal nachschlagen.

Fläche $A$ = Seitenlänge $a$ $\cdot$ Seitenlänge $b$

Fläche $A$ = $\frac{\text{ Grundseite } g \cdot \text{ Höhe zur Grundseite } h_g}{2}$

Aufgabe 7: Rechnen

Berechne die Grundfläche, die Mantelfläche und die Oberfläche in den beiden Aufgaben:
a) Prisma mit der Grundfläche eines Dreiecks: $a=2{,}5$ cm, $b=2{,}6$ cm, $c=2{,}16$ cm und der Höhe des Dreiecks $h_a=2$ cm und mit der Körperhöhe $h=12$ cm des Prisma.

Zeichnet euch den Körper auf.

Berechnung der Grundfläche:
$\begin{align} G = \frac{a \cdot h_a}{2} = \frac{2 \text{ cm} \cdot 2,5 \text{ cm}}{2} = 2,5 \text{ cm}^2. \end{align}$
A: Der Flächeninhalt einer Grundfläche beträgt $2,5 \text{ cm}^2$.
Berechnung der Mantelfläche:
$\begin{align} M = a \cdot h + b \cdot h + c \cdot h = 2{,}5 \text{ cm} \cdot 12 \text{ cm} + 2{,}6 \text{ cm} \cdot 12 \text{ cm} + 2{,}16 \text{ cm} \cdot 12 \text{ cm} = 30 \text{ cm}^2 + 31{,}2 \text{ cm}^2 + 25{,}92 \text{ cm}^2 = 87{,}12 \text{ cm}^2. \end{align}$
A: Der Flächeninhalt der Mantelfläche beträgt $87{,}12 \text{ cm}^2$ .
Berechnung der Oberfläche:
$\begin{align} O = 2 \cdot G + M = 2 \cdot 2{,}5 \text{ cm}^2 + 87{,}12 \text{ cm}^2 = 92{,}12 \text{ cm}^2. \end{align}$

A: Der Oberflächeninhalt beträgt $92{,}12 \text{ cm}^2$.

b) Prisma mit der Grundfläche eines Parallelogramm: $a=8$ cm, $b=5$ cm , $h_a=4{,}5$ cm und mit der Körperhöhe $h=9$ cm des Prisma.

Zeichnet euch den Körper auf.

Berechnung der Grundfläche:
$\begin{align} G = a \cdot h_a = 8 \text{ cm} \cdot 4{,}5 \text{ cm} = 36 \text{ cm}^2. \end{align}$
A: Der Flächeninhalt einer Grundfläche beträgt $36 \text{ cm}^2$.
Berechnung der Mantelfläche:
$\begin{align} M = 2 \cdot a \cdot h + 2 \cdot b \cdot h = 2 \cdot 8 \text{ cm} \cdot 9 \text{ cm} + 2 \cdot 5 \text{ cm} \cdot 9 \text{ cm} = 144 \text{ cm}^2 + 90 \text{ cm}^2 = 234 \text{ cm}^2. \end{align}$
A: Der Flächeninhalt der Mantelfläche beträgt $234 \text{ cm}^2$.
Berechnung der Oberfläche:
$\begin{align} O = 2 \cdot G + M = 2 \cdot 36 \text{ cm}^2 + 234 \text{ cm}^2 = 306 \text{ cm}^2. \end{align}$

A: Der Oberflächeninhalt beträgt $306 \text{ cm}^2$.

Aufgabe 8: Berechne die fehlende Größe

Bei einem Prisma sind $G$ der Flächeninhalt einer Grundfläche, $M$ der Mantelflächeninhalt und $O$ der Oberflächeninhalt. Berechne die fehlende Größe. Es seien

$O = 18$ dm² und
$G = 250$ cm².

Schreibe zunächst die Formel für den Oberflächeninhalt auf.

Stelle die Gleichung für den Oberflächeninhalt nach $M$ um.

Die Größen auf eine Maßeinheit bringen:
$\begin{align} O &= 18 \text{ dm}^2 = 1800 \text{ cm}^2 \\ G &= 2{,}5 \text{ dm}^2 = 250 \text{ cm}^2 \end{align}$

Einsetzten der bekannten Größen in die bekannte Gleichung und anschließend wird nach $M$ umgestellt:

$\begin{align} &\quad& O &= 2 \cdot G + M \\ &\Leftrightarrow& 1800 \text{ cm}^2 &= 2 \cdot 250 \text{ cm}^2 + M \\ &\Leftrightarrow& 1800 \text{ cm}^2 &= 500 \text{ cm}^2 + M \\ &\Leftrightarrow& 1300 \text{ cm}^2 &= M \\ &\Leftrightarrow& 1300 \text{ cm}^2 &= M \end{align}$

Damit ist die fehlende Größe $M = 1300 \text{ cm}^2 = 13 \text{ dm}^2$.

Aufgabe 9: Vermutung anstellen

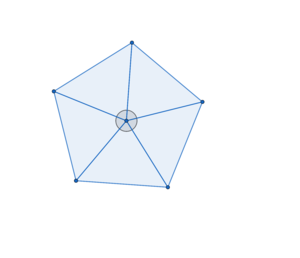
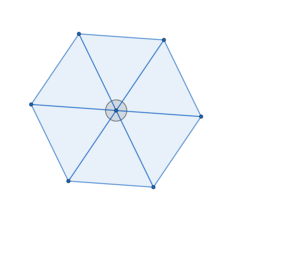
Betrachte das Fünfeck und das Sechseck. Welche Regelmäßigkeiten vermutest du für beliebige $n$-Ecke im Hinblick auf die Flächenberechnung?

Fünfeck

Sechseck

1. Man kann jedes regelmäßige $n$-Eck in $n$ gleiche Dreiecke unterteilen.

2. Wenn die Länge der Grundlinie bekannt ist, kann man nach Bestimmung des Mittelpunkts und dessen Abstand zum Mittelpunkt der Grundlinie den Flächeninhalt jeden Dreiecks bestimmen.

Berechnung der Oberfläche eines Prismas mit regelmäßigem $n$-Eck als Grundfläche

Die Oberfläche jeden Prismas berechnet sich durch die Addition der zwei Grundflächen und der $n$ Seitenflächen. Mathematisch ausgedrückt:

Oberflächeninhalt $O$ = Grundflächeninhalt 1 + Grundflächeninhalt 2 + Rechteckflächeninhalt 1 + Rechteckflächeninhalt 2 + ... + Rechteckflächeninhalt $n$

Die Grundflächeninhalte sind nach Definition eines Prismas beide gleich groß. Besonderheit: Wegen des regelmäßigen $n$-Ecks als Grundfläche haben die $n$ Rechtecke den gleichen Flächeninhalt. Darum dürfen wir zusammenfassen und es ergibt sich die allgemeine Formel

Oberflächeninhalt = 2 $\cdot$ Grundflächeninhalt + $n$ $\cdot$ Rechteckflächeninhalt bzw. $O$ = 2 $\cdot$ $G$ + $n$ $\cdot$ $A$

Fläche $n$-Eck $A_n$ = Fläche Dreieck $A_D$ $\cdot$ Anzahl Dreiecke im $n$-Eck $n$ = $\frac{ \text{Grundseite } g \cdot \text{ Höhe zur Grundseite } h_g}{ 2}$ $\cdot$ $n$

Mantelfläche $M$ = Fläche Rechteck $A$ $\cdot$ Anzahl Seiten des $n$-Ecks $n$

= Seitenlänge $a$ $\cdot$ Seitenlänge $b$ $\cdot$ $n$

Volumen eines Prismas

Hinweis

In diesem Abschnitt beschäftigst du dich mit dem Volumen eines Prismas. Du berechnest den Rauminhalt eines Prismas, indem du den Flächeninhalt einer Grundfläche mit der Höhe des Prismas multiplizierst. Du kannst dir hier einen Körper vorstellen, den man mit Wasser oder anderen Materialien füllt, umgangssprachlich einen massiven Körper.

Erinnerung

Falls du einige der Grundlagen nicht mehr weißt, kannst du die Formeln hier nochmal nachschlagen.

Volumen $V_W$ = Seitenlänge $a$ $\cdot$ Seitenlänge $a$ $\cdot$ Seitenlänge $a$

Volumen $V_Q$ = Seitenlänge $a$ $\cdot$ Seitenlänge $b$ $\cdot$ Seitenlänge $c$

Volumen $V_P$ = Grundfläche $G$ $\cdot$ Körperhöhe $h$

Aufgabe 10: Rechnen

Berechne das Volumen der beiden Körper:
a)Prisma mit der Grundfläche eines Dreiecks: $a=2{,}5$ cm, $b=2{,}6$ cm, $c=2{,}16$ cm und der Höhe des Dreiecks $h_a=2$ cm und mit der Körperhöhe $h=12$ cm des Prisma.

Schaue dir Aufgabe 7 a) an.

Berechnen des Volumens:
$\begin{align} V = G \cdot h = 2,5 \text{ cm}^2\cdot 12 \text{ cm} = 30\text{ cm}^3. \end{align}$

A: Das Volumen beträgt $30 \text{ cm}^3$.

b) Prisma mit der Grundfläche eines Parallelogramm: $a=8$ cm, $b=5$ cm , $h_a=4{,}5$ cm und mit der Körperhöhe $h=9$ cm des Prisma.

Schaue dir Aufgabe 7 b) an.

Berechnen des Volumens:
$\begin{align} V = 36 \text{ cm}^2 \cdot 9 \text{ cm} = 324 \text { cm}^3 \end{align}$

A: Das Volumen beträgt $324 \text{ cm}^3$.

Aufgabe 11: Berechne die fehlenden Größen

Bei einem Prisma sind $G$ der Flächeninhalt einer Grundfläche, $M$ der Mantelflächeninhalt, $O$ der Oberflächeninhalt, $h$ die Höhe und $V$ das Volumen des Körpers. Berechne die fehlenden Größen.

$\begin{align} O &= 35 \text{ dm}^2, \\ M &= 2800 \text{ cm}^2 \text{ und} \\ V &= 35000 \text{ cm}^3. \end{align}$

Schreibe zunächst die Formel für den Oberflächeninhalt auf.

Stelle die Gleichung für den Flächeninhalt nach $G$ um.

Mache das Gleiche mit der Formel für das Volumen.

Die Größen auf eine Maßeinheit bringen:

$\begin{align} O = 35 \text{ dm}^2 = 3500 \text{ cm}^2 \\ \end{align}$

Einsetzen der bekannten Größen in die bekannte Gleichung und anschließend wird nach $G$ umgestellt:

$\begin{alignat}{2} &\quad& O &= 2 \cdot G + M \\ &\Leftrightarrow& \ 3500 \text{ cm}^2 &= 2 \cdot G + 2800 \text{ cm}^2\\ &\Leftrightarrow& \ 700 \text { cm}^2 &= 2 \cdot G \\ &\Leftrightarrow& \ G &= 350 \text{ cm}^2 \end{alignat}$

Einsetzten der bekannten Größen in die bekannte Gleichung und anschließend wird nach $h$ umgestellt:

$\begin{alignat}{2} &\quad& V &= h \cdot G \\ &\Leftrightarrow& 35000 \text{ cm}^3 &= h \cdot 350 \text{ cm}^2\\ &\Leftrightarrow& 100 \text{ cm} &= h \end{alignat}$

A: Die Höhe beträgt $100 \text{ cm}$ und die Grundfläche ist $350 \text{ cm}^2$.

Ausblick

Hinweis

In diesem Abschnitt beschäftigst du dich mit weiterführenden Inhalten, die später wichtig werden können. Zum Beispiel gibt es auch Prismen mit unregelmäßigen Grundflächen. Außerdem wirst du auch schräge Prismen kennenlernen, die dann aber eine etwas abgeänderte Definition bei Prismen erfordern.

Aufgabe 12: Unregelmäßige Grundflächen

Du hast bereits mit Prismen mit unregelmäßiger Form der Grundflächen gearbeitet, dir darüber aber kaum Gedanken gemacht, weil du rechtwinklige Dreiecke oder Parallelogramme kennst und recht einfach berechnen kannst. Aber es gibt auch kompliziertere Fälle. Viele von diesen sind Kombinationen bekannter Flächen, z. B. unterschiedlichen Rechtecken und/oder Dreiecken. Später kann es sehr wichtig werden, diese unregelmäßigen Grundflächen zur leichteren Berechnung wieder in einzelne Teilflächen zu zerlegen. Finde im Applet zur passenden unregelmäßigen Grundform eine mögliche Zerlegung und "klebe" sie aneinander! Bist du fertig, klicke auf das blaue Häkchen unten rechts.

Aufgabe 13: Gedankenexperiment

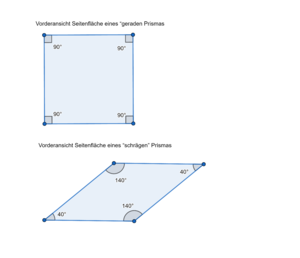
Stelle dir vor, du hast vier gleiche Kartenspiele. 1. Schritt: Du stapelst sie genau übereinander und erhälst dadurch ein Prisma! 2. Schritt: So gerade nach oben findest du es aber langweilig, deshalb verschiebst du jede einzelne Karte immer ein wenig mehr auf eine Seite und bringst so den Stapel in eine Schräge. Du bekommst so ein schräges Prisma! Frage: Was verändert sich? Was bleibt gleich? Bist du fertig, klicke auf das blaue Häkchen unten rechts.

Gleich bleiben Winkel in den Grundflächen, da wir die oberste und unterste Karte nicht verändern und sie "Rechtecke" bleiben. Das Volumen bzw. die Höhe würden sich nur ändern, wenn man Karten wegnimmt oder dazulegt.

Die veränderte Form des Körpers bzw. der Oberfläche ist eine logische Folge der Verschiebungen der Karten, was du auch auf dem zweiten Bild der Hilfe sehen kannst. Bei den bisher bekannten "geraden" Prismen haben wir zwischen Grundflächen und Seitenflächen immer rechte Winkel von 90°. Bei "schrägen" Prismen muss es aber Winkel geben, die ungleich 90° sind.