Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel

Aus ZUM Projektwiki

Seite im Aufbau

zurück zur Seite der Herta-Lebenstein-Realschule


5 Rauminhalt (Volumen) von Quader und Würfel

Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.

Schätzfrage
Juice-g2db3a4596 1280.png
Wie viel Flüssigkeit passt in das Trinkpäckchen?

Wie viele Kubikzentimeterwürfel passen hinein?

Schätze.

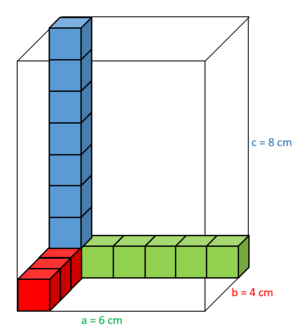
Um deine Schätzung zu prüfen, lege das Päckchen mit kleinen Kubikzentimeterwürfeln aus:
Trinkpäckchen 1.jpg
Trinkpäckchen 2.jpg Es passen 6 Würfel in eine Reihe.
Trinkpäckchen 3.jpg Es passen 4 Reihen in den Boden.
Trinkpäckchen 4.jpg Es passen ca. 8 Schichten übereinander.


Nutze das nachfolgende GeoGebra-Applet, um herauszufinden, wie du mit diesen Angaben das Volumen des Trinkpäckchens berechnen kannst:

GeoGebra

Applet von Matthias Hornof Originallink: https://www.geogebra.org/m/EcHrrMaC


Rauminhalt (Volumen) eines Quaders
Volumen Quader Würfel eingezeichnet.png
Den Rauminhalt (das Volumen) berechnen wir mit der Formel:  

V = Länge ∙ Breite ∙ Höhe
    =  a ∙ b ∙ c

Beim Würfel rechnen wir also:
V = Länge ∙ Breite ∙ Höhe
    =  a ∙ a ∙ a
    = a³

Das Volumen des Trinkpäckchens beträgt also
V = a ∙ b ∙ c
    =  6 ∙ 4 ∙ 8

    = 192 (cm³)

Da die Höhe des Trinkpäckchens etwas höher als 8 cm ist (nämlich 8,5cm), beträgt das tatsächliche Volumen 204 cm³, also ist die Inhaltsangabe von 200 ml richtig.

Video laden
YouTube
Video laden
YouTube


Übung 1

Löse auf der Seite realmath so viele Aufgaben, bis du mindestens 300 Punkte gesammelt hast.
Tipp: Du kannst durch Ziehen an den Punkten den Quader mit Kubikzentimeterwürfeln ausfüllen.



Übung 2

Löse die Aufgaben aus dem Buch. Achte auf eine übersichtliche Darstellung. Schreibe die Kantenlängen des Quaders auf. Notiere die Formel, setze die Werte ein und berechne. Denke an die passende Einheit.

  • S. 93 Nr. 5
  • S. 93 Nr. 4
Lifesaver-34525 1280.png

Stelle die Schieberegler passend zur Aufgabe ein und kontrolliere deine Rechnung.
Originallink: https://www.geogebra.org/m/ytgp88hk

GeoGebra


Übung 3 Nachdenkaufgabe

Wie ändert sich das Volumen eines Würfels, wenn man die Kantenlängen verdoppelt?

Stelle eine Vermutung auf und überprüfe sie an einem Beispiel bzw. nutze das Applet unten.
GeoGebra



Übung 4 Kantenlänge eines Quaders berechnen

Du kannst bei gegebenem Volumen auch eine fehlende Kantenlänge berechnen. Nutze dazu die Umkehraufgabe.
geg: V = 60 cm³; a = 5 cm; b = 3 cm
ges: c
V = a ∙ b ∙ c   |Werte einsetzen
60 = 5 ∙ 3 ∙ c
60 = 15 ∙ c   |:15 Umkehraufgabe 60 : 15 = c
60 : 15 = c
4 (cm) = c

  • S. 93 Nr. 6 b, c, d
  • S. 95 Nr. 15
Lifesaver-34525 1280.png

Stelle die Schieberegler passend zur Aufgabe ein und kontrolliere deine Rechnung.
Originallink: https://www.geogebra.org/m/ytgp88hk

GeoGebra

Stelle die Schieberegler so ein, dass das Volumen V = 180cm³ beträgt. Beobachte die Oberfläche O. Was fällt dir auf?
Originallink https://www.geogebra.org/m/ebc8chmj

GeoGebra

Anwendungsaufgaben

Um Anwendungsaufgaben lösen zu können, musst du die Begriffe "Oberfläche und Volumen" verstanden haben.
Prüfe dein Wissen, indem du den Situationen den passenden Begriff zuordnest.


Übung 5 Anwendungsaufgaben

Löse die Aufgaben aus dem Buch. Notiere zunächst, welche Größen gegeben und welche gesucht sind. Eine Skizze hilft dir.

  • S. 95 Nr. 17
  • S. 95 Nr. 18
  • S. 93 Nr. 3
  • S. 93 Nr. 7
Lifesaver-34525 1280.png

a) geg: a=12m; b=8m; c=1,5m
ges: V
Du berechnest das Volumen in m³. Wandel das Ergebnis anschließend in dm³ um, dann erhältst du die Angabe in Litern.

b) Wenn der Wasserstand auf 2m erhöht werden soll, steigt die ursprüngliche Höhe also um 0,5m, denn 2m-1,5m = 0,5m.

a) Berechne das Volumen des Klassenzimmers.
Jede Person benötigt 6m³ Luft, teile also das Volumen durch 6.
b) Wie groß muss das Volumen sein, wenn 28 Kinder im Raum sind und jedes Kind 6 m³ Luft benötigt?

Finde anschließend passende Maße für die Länge und Breite des Raumes, die Höhe des Klassenzimmers beträgt in der Regel 3m.
Hier ist die Größe der Goldfolie gesucht, dies entspricht der OBERFLÄCHE des Quaders.

1. Tipp: Wandle alle Maße in dieselbe Einheit um. Wähle die Einheit dm, dann berechnest du das Volumen direkt in dm³, also in Liter.
2. Tipp: Das das Aquarium nur bis 5cm unter den Rand gefüllt wird, musst du die Höhe c berechnen.

(c = 5dm - 5cm = 5dm - 0,5dm = 4,5dm)



Vermischte Übungen - online
Bearbeite die Aufgaben auf der Seite Aufgabenfuchs zur Berechnung des Volumens und der Oberfläche von Quader und Würfel.
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Flächeninhalt_und_Rauminhalt/Rauminhalt_von_Quader_und_Würfel&oldid=77937“