Benutzer:Buss-Haskert/AFR/Lineare Gleichungssysteme
1) Lineare Gleichungen mit zwei Variablen
2) Lineare Gleichungssysteme
3) Lineare Gleichungssysteme zeichnerisch lösen
Diese Seite wurde kopiert aus dem Lernpfad der Herta-Lebenstein-Realschule, erstellt von C. Buß-Haskert [1] unter der CC BY SA Linzenz. Herzlichen Dank!
0) Vorwissen
| Ich kann ... | Übungen online |
|---|---|
| - mit Fachbegriffen umgehen. |
|
| -Terme zu mathematische Texten, geometrischen Situationen
und Sachsituationen aufstellen. |
|
| - Werte von Termen berechnen. |
|
| -Terme (mit Klammern) vereinfachen |
|
| -Lineare Gleichungen lösen. |
|
| - eine Wertetabelle zu einer linearen Funktion aufstellen |
|
| -Gleichung und Graphen linearer Funktionen einander zuordnen. |
|
1) Lineare Gleichungen mit zwei Variablen
GeoGebra-Applet zur Einsteigsaufgabe: https://www.geogebra.org/m/wwaferxp

von C. Buß-Haskert
Addiert man zu einer Zahl 6, so erhält man das Dreifache der anderen Zahl.x + 6 = 3∙y
Addiert man zur zweiten Zahl 6, so erhält man das Vierfache der ersten Zahl.y + 6 = 4∙x
Die Summe zweier Zahlen ist 52.x + y = 52
Das Doppelte der ersten ist gleich dem Dreifachen der zweiten Zahl.2∙x = 3∙y
Ein gleichschenkliges Dreieck hat einen Umfang von 41 cm.2x + y = 41
In einem gleichschenkligen Dreieck ist die Basis (Grundseite) nur ein Drittel so lang wie die Schenkel.y = x
Der Umfang eines Rechtecks ist 80 cm.2x + 2y = 80
Der Flächeninhalt eines Rechtecks beträgt 64cm².x∙y = 64
Andreas hat 6 CDs mehr als Karin.y = x - 6
Setze die Zahlenpaare passend in die Gleichung ein und prüfe, ob sich eine wahre Aussage ergibt (Punktprobe).
Beispiel:
(1|-6) einsetzen in a):
1 + (-6) = 8
1 - 6 = 8
-5 = 8 (f)
Setze die gegebenen Werte passend in die Gleichung ein und berechne die fehlende Zahl des Zahlenpaares.
Beispiel:
(-2|___) einsetzen in a):
2·(-2) + y = 6
-4 + y = 6 |+4
y = 10 (f)
Erinnerung: Graphen linearer Funktionen zeichnen - Video
Beispiel: Aufgabenteil a)
4x + 2y = 10
1. Gleichung nach y auflösen:
4x + 2y = 10 |-4x
2y = -4x + 10 |:2
y = -2x + 5
2. Graphen zeichen:
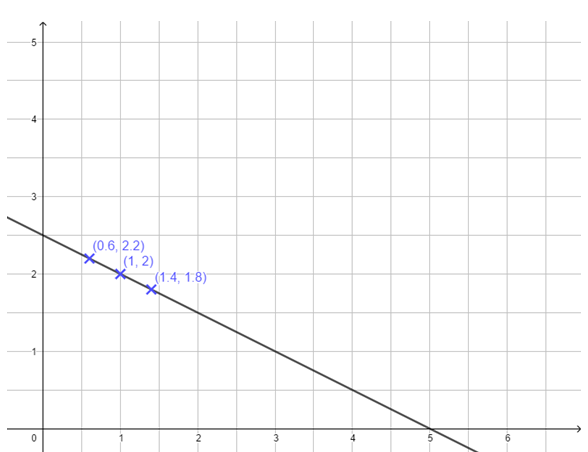
y = -2x + 5 schneidet die y-Achse im Punkt P(0|5) und hat die Steigung m = -2.
Zeichne passend. (Hilfe: GeoGebra).
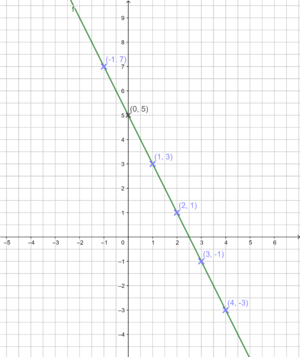
Probe durch Rechnung:
(-1|7) ist Lösung der Gleichung 4x + 2y = 10, denn
4·(-1) + 2·7 = 10
-4 + 14 = 10
10 = 10 (w)
1. Bedeutung der Variablen angeben:
x Anzahl der Weizenbrötchen
y Anzahl der Roggenbrötchen
2. Gleichung aufstellen:
x·0,30 + y·0,50 = 24
3. Mögliche Lösung angeben:
GeoGebra-Applet zur Aufgabe
Originallink https://www.geogebra.org/m/v6fs4e6u

Applet von C.Buß-Haskert
2) Lineare Gleichungssysteme
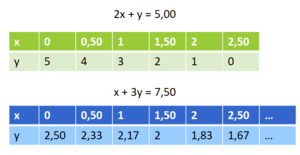
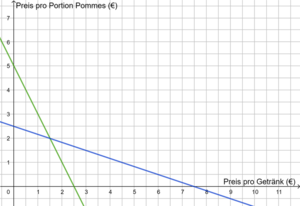
Lege die Bedeutung der Variablen fest, z.B. x - Preis pro Getränk, y - Preis pro Portion Pommes.
Stelle nun jeweils eine passende Gleichung auf. Nutze zur Lösung verschiedene Darstellungen: Wertetabellen und Graphen
I. 2x + y = 5,00
II. x + 3y = 7,50