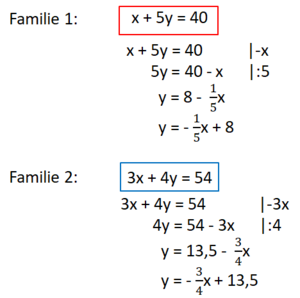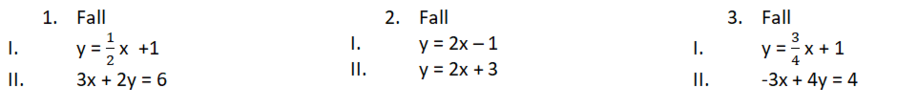Benutzer:Buss-Haskert/AFR/Lineare Gleichungssysteme/Lineare Gleichungssysteme zeichnerisch lösen
3) Lineare Gleichungssysteme zeichnerisch lösen
Lege die Bedeutung der Variablen fest, z.B. x - Preis pro Erwachsener, y - Preis pro Kind.
Stelle nun jeweils eine passende Gleichung auf. Nutze zur Lösung verschiedene Darstellungen: Wertetabellen und Graphen.
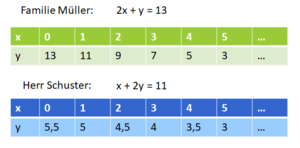
I. 2x + y = 13
II. x + 2y = 11
Wo findest du die Lösung des Problems? Begründe.
Wo findest du die Lösung des Problems? Begründe.
Das Video fasst die Schritte noch einmal zusammen:
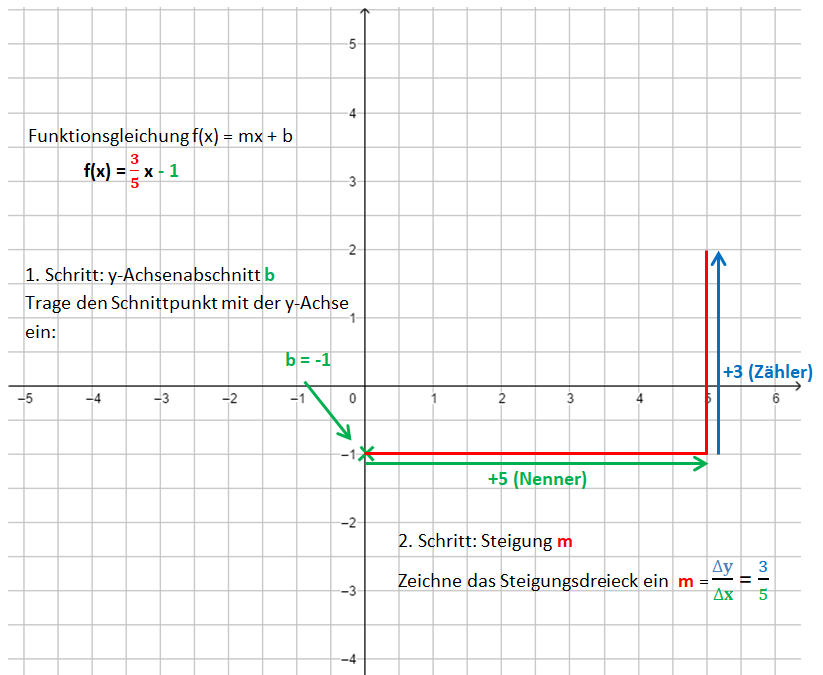
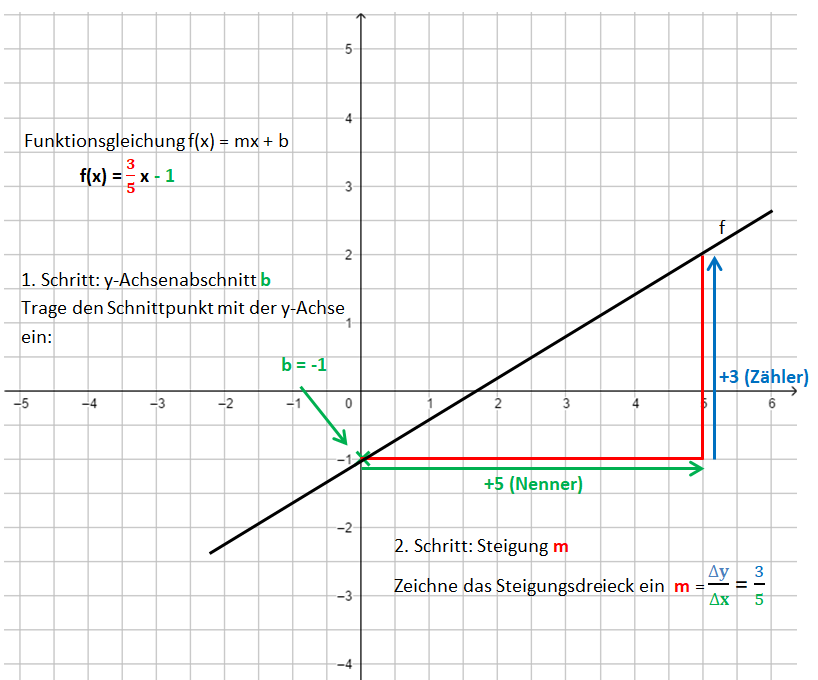
Wie zeichne ich den Graphen, wenn die Funktionsgleichung gegeben ist?
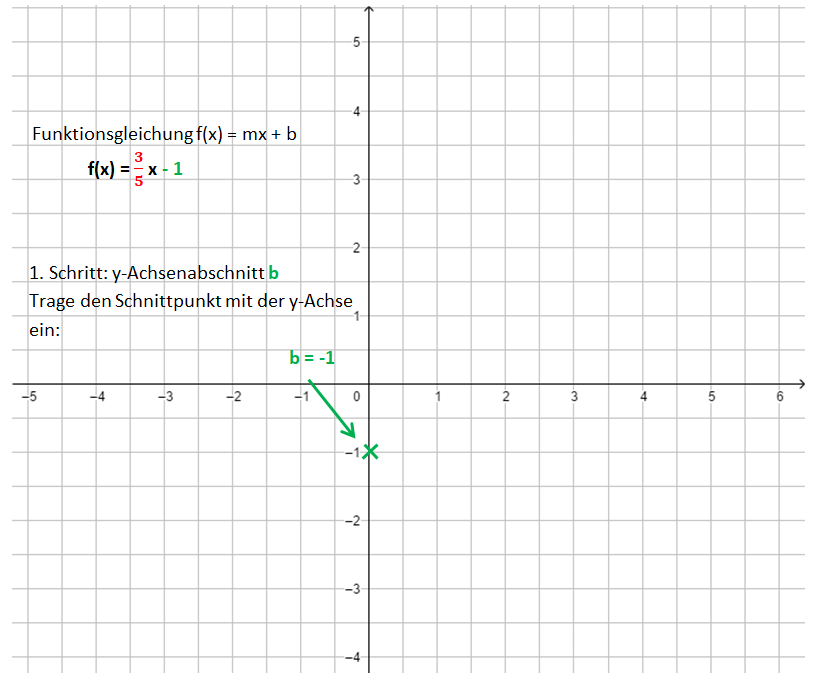
1. Schritt: Zeichne den y-Achsenabschnitt b ein: P(0|b)
2. Schritt: Zeichne das Steigungsdreieck ein. Starte im Punkt P. Der Nenner gibt an, wie viele Einheiten du nach rechts gehst, der Zähler, wie viele Einheiten nach oben (unten).
3. Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Wie zeichne ich den Graphen zu einer Funktionsgleichung: Videos
Lösung zu S.46 Nr. 3a Schritt für Schritt:
Originallink: https://www.geogebra.org/m/hmvzwfan
Die LearningApps enthalten die Lösungsschritte. Bringe sie in die richtige Reihenfolge und vergleiche deine Lösung.
Stelle die Gleichungen zunächst nach y um.
1. Gleichung:
-x + 2y = 1 |+x
2y = x + 1 |:2
y = x +
Zeichne die Gerade zur 1. Gleichung.
2. Gleichung:
2x - y = 4 |-2x
-y = -2x + 4 |:(-1)
y = 2x - 4
Zeichne die Gerade zur 2. Gleichung.
direkter Link: https://www.geogebra.org/m/kb3en6sj
Applet von just01120
Löse schrittweise, wie oben beschrieben:
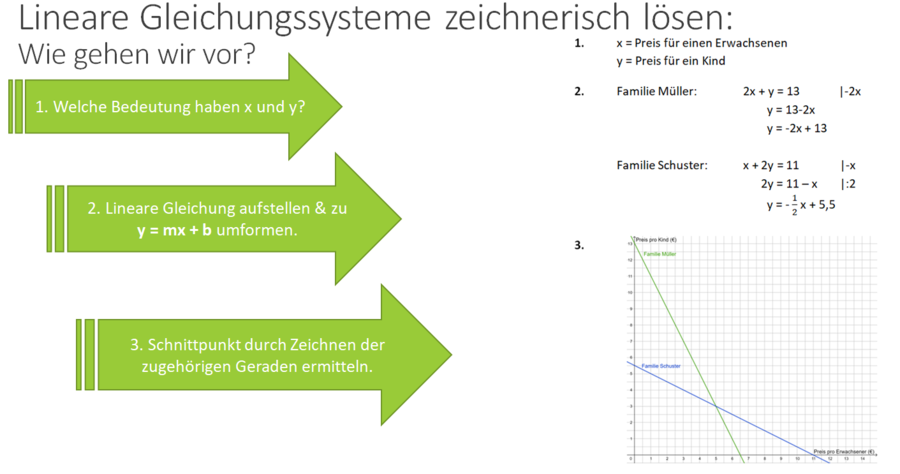
1. Lege die Bedeutung der Variablen fest
2. Stelle zwei lineare Gleichungen auf und forme sie so um, dass sie die Form y=mx+b haben.
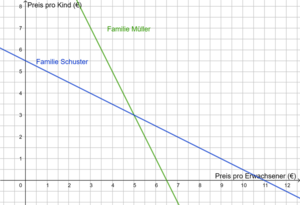
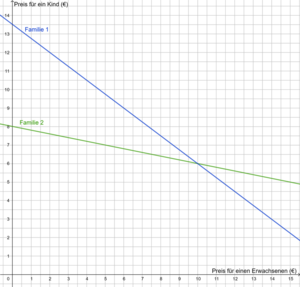
3. Zeichne die zugehörigen Graphen in ein Koordinatensystem und lies den Schnittpunkt ab. Die Koordinaten des Schnittpunktes sind die Lösung des Gleichungssystems.
x = Preis für einen Erwachsenen
y = Preis für ein Kind
Löse schrittweise, wie oben beschrieben:
1. Lege die Bedeutung der Variablen fest
2. Stelle zwei lineare Gleichungen auf und forme sie so um, dass sie die Form y=mx+b haben.
3. Zeichne die zugehörigen Graphen in ein Koordinatensystem und lies den Schnittpunkt ab. Die Koordinaten des Schnittpunktes sind die Lösung des Gleichungssystems.
x Anzahl der Dreibettzimmer
y Anzahl der Fünfbettzimmer
2. Schritt: Gleichungen aufstellen und in eine Funktionsgleichung umformen
Es gibt insgesamt 35 Zimmer, also gilt
I. x + y = 35
Es gibt insgesamt 145 Jugendliche, diese werden zu dritt (pro Dreibettzimmer) bzw. zu fünft (pro Fünfbettzimmer) aufgeteilt, also gilt
II. 3x + 5y = 145
3. Schritt: Graphen zeichnen und Schnittpunkt bestimmen
I. y = -x + 35
II. y = -x + 29
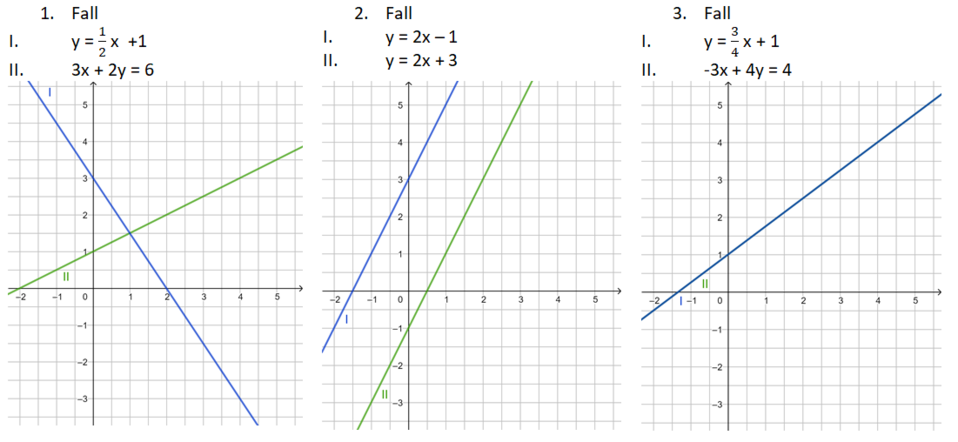
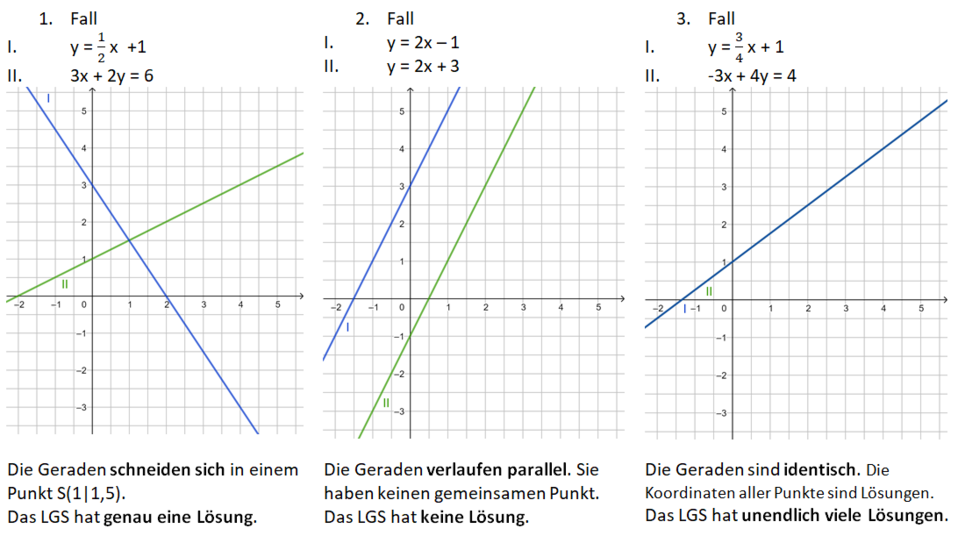
Anzahl der Lösungen linearer Gleichungssysteme
Um ein Gleichungssystem zeichnerisch lösen zu können, musst du die Gleichungen in die Form y = mx + b bringen. Dann kannst du die Geraden mit dem y-Achsenabschnitt b und dem Steigungsdreieck (für m) zeichnen.
Beim 2. Fall sind die Gleichungen schon in der Form y = mx+b gegeben.
