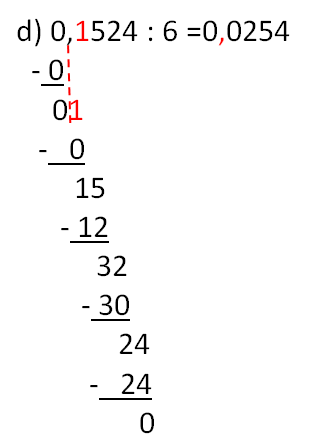Herta-Lebenstein-Realschule/Lernpfad Rechnen mit Dezimalbrüchen/3) Dezimalbrüche dividieren

zurück zur Seite der Herta-Lebenstein-Realschule

1) Dezimalbrüche addieren und subtrahieren

3) Dezimalbrüche dividieren

Die letzte Frage zum Weitsprung, die wir gestellt haben ist, wie weit Tom durchschnittlich in allen 3 Sprüngen gesprungen ist.

Beginnen wir mit einer leichteren Frage:

Dividieren durch 10, 100, 1000

Wie kannst du den Durchschnitt von 10 Sprüngen berechnen, wenn die gesamte Sprungweite 32,40 m betragen hätte?

Das kannst du sicher im Kopf berechnen. Fällt dir etwas auf?

3.1 Division durch 10, 100, 1000

Division durch 10, 100, 1000

Beim Dividieren durch 10, 100, 1000 (Zehnerpotenzen) wird das Komma nach links verschoben. Es wird um so viele Stellen verschoben, wie die Zehnerpotenz Nullen hat.

Schau das Erklärvideo an:

Übung 1: Dividieren durch Zehnerpotenzen

Bearbeite die folgende App und danach S. 124 Nr. 4 im Heft.

Frage

Wie weit ist Tom durchschnittlich gesprungen, wenn er die Ergebnisse 3m; 3,2m und 3,95m erreichte? Wie können wir vorgehen?

Dafür musst du die Summe von 3m + 3,2m + 3,95 m = 10,15 m durch 3 teilen. Wie teilen wir einen Dezimalbruch durch eine natürliche Zahl?

Die Regel dazu kennst du schon vom Umwandeln von Brüchen in Dezimalbrüche durch Division.

Erinnerung: 2. Möglichkeit im Kapitel 3

3) Brüche in Dezimalbrüche umwandeln

3.2) Division durch eine natürliche Zahl

Dezimalbrüche durch eine natürliche Zahl dividieren

Wir dividieren einen Dezimalbruch durch eine natürliche Zahl, indem wir wie mit natürlichen Zahlen rechnen und beim Überschreiten des Kommas auch ein Komma im Ergebnis setzen.

Ergänze die Lücken mit den unverdrehten Wörtern!

Sobald wir bei der schriftlichen Division Ziffern nach dem Komma herunterholen, muss auch im Ergebnis ein Komma gesetzt werden.

Jetzt können wir unsere Ausgangsfrage beantworten:

Das Video erklärt dies noch einmal anhand eines weiteren Beispiels:

Übung 2: Kopfrechnen

Löse die nachfolgenden Aufgaben im Kopf. Kontrolliere dein Ergebnis mit der Probe.

Übung 3: Division durch eine natürliche Zahl

Berechne Buch S. 134 Nr. 12a,b,d

Die Lösung beginnt mit 0,0... Falls dieser Tipp nicht ausreicht, schau auf die Beispielrechnung.

Lösungen zum Vergleichen (Du musst ausführliche Rechnungen im Heft notiert haben!)

a) 5,0375; 31,875; 56,3

b) 4,525; 6,7; 0,27

d) 0,0254; 0,1251; 0,1123

3.3) Division durch einen Dezimalbruch

Division durch einen Dezimalbruch

Beim Dividieren eines Dezimalbruches durch einen Dezimalbruch müssen wir in zwei Schritten vorgehen:

1. Verschiebe bei Dividend und Divisor das Komma um so viele Stellen nach rechts, bis der Divisor eine natürliche Zahl ist.

2. Dann können wir wie bekannt rechnen (...beim Überschreiten des Kommas auch ein Komma im Ergebnis setzen).

Das folgende Video erklärt dies anhand einiger Beispiele.

Übung 4: Division durch einen Dezimalbruch (online)

Übe auf der Seite realmath so lange, bis du mindestens 300 Punkte erreicht hast.

Übung 5: Division durch einen Dezimalbruch

Löse Buch S. 134 Nr. 18 schriftlich im Heft. Schreibe die Aufgabe ab, verschiebe das Komma so weit wie nötig und rechne dann schriftlich.

Lösungen zum Vergleichen (Du musst ausführliche Rechnungen im Heft haben!)

a) 2,7; 3,64; 5,3

b)34,6; 23,7; 45,3

c) 2,56; 5,68;3,47

d)25; 65; 210

e) 56,5; 0,58; 0,56

f) 12,5; 2,625; 2,625

4) Verbindung der Rechenarten

IDEENSAMMLUNG

FLINK-Team auf GeoGebra: https://www.geogebra.org/m/we7v53xn
Originallink: https://www.geogebra.org/m/ymnwmkzj

Übungen:
Originallink: https://www.geogebra.org/m/ymnwmkzj

Originallink: https://www.geogebra.org/m/rpaxx8zk

Originallink: https://www.geogebra.org/m/ancmatnm

Originallink: https://www.geogebra.org/m/mbadqpdc

Originallink: https://www.geogebra.org/m/yshdjawq

Applets des FLINK-Teams

zurück zur Startseite

4) Anwendungsaufgaben

Suche

Herta-Lebenstein-Realschule/Lernpfad Rechnen mit Dezimalbrüchen/3) Dezimalbrüche dividieren

Inhaltsverzeichnis