Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Die Ableitung im Sachkontext

Auf dieser Seite findest du Aufgaben, die dein Verständnis zum Sachkontext von Ableitungen vertiefen sollen. Du wiederholst, Ergebnisse im Sachzusammenhang zu interpretieren, Signalwörter in den Aufgabenstellungen zu erkennen und diese mit den entsprechenden rechnerischen Vorgehensweisen zu verknüpfen. Außerdem vertiefst du an verschiedenen Beispielen den Zusammenhang zwischen der Funktion und den einzelnen Ableitungen. Dies tust du vor allem mit Bezug auf die Einheiten der Funktionswerte. Die Aufgaben 1-3 dienen als Einstieg und sind leichter zu lösen. In den Aufgaben 4-5 kannst du schwierigere Probleme lösen. Falls du dich schon sehr sicher fühlst, kannst du dich an die letzte Aufgabe begeben.

Aufgabe 1: durchschnittliche Änderungsrate im Sachzusammenhang

Aufgabe 1: Dieselpreise

{{{2}}}

Aufgabe 2: Wiederholung wichtiger Signalwörter

Aufgabe 2: Zuordnen

{{{2}}}

Aufgabe 3: Funktionswerte und Ergebnisse im Sachzusammenhang deuten

Aufgabe 3: Silvesterkracher

{{{2}}}

Aufgabe 4: Einheiten der Ableitungsfunktion

Aufgabe 4: Aussagen der Ableitungsfunktion und Änderung der Einheiten

{{{2}}}

Aufgabe 5: Funktionsuntersuchung

Aufgabe 5 : Ein Tag im Zoo

{{{2}}}

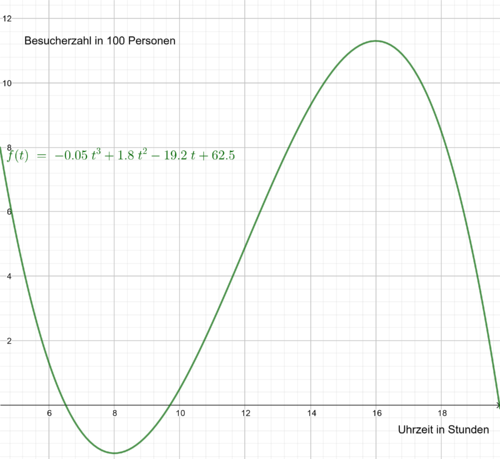
Ein Zoo ist bekanntermaßen in den Sommerferien am besten besucht. Die Besucherzahlen (in 100 Personen) eines bestimmten Zoos können durch die Funktion
b(t) = - 0,05 t³ + 1,8 t² - 19,2 t + 62,5 für 10 < t ≤ 19,5
näherungsweise beschrieben werden. Dabei gibt t die Uhrzeit in Stunden an.

Abb. 5.1: Besucherzahl eines Zoos

Rechne die folgenden Aufgaben im Heft und vergleiche mit den angegebenen Lösungsvorschlägen.
a) Zu welcher Uhrzeit befinden sich am meisten Besucher in dem Zoo? Und wie viele sind es?
<popup name="Tipp">Die Ableitung lautet: b´(t) = - 0,15 t² + 3,6 t - 19,2 </popup> <popup name="Lösung">Die Nullstellen der Ableitung entsprechen den Maximalstellen der Normalfunktion. Setzt man die Ableitung gleich 0, also 0 = b´(t) = - 0,15 t² + 3,6 t - 19,2 , dann erhält man $t_1$ = 8 und $t_2$ = 16. Da der Zoo erst um 10:00 Uhr (also t = 10) öffnet, ist $t_2$ die einzige Lösung.
Setzt man das in die Funktion ein erhält man: b(16) = 11,3 . Da die Besucherzahlen in 100 Personen angegeben werden, ergibt sich die Lösung, wenn man 11,3 mit 100 multipliziert.
Die Antwort: Mit 1130 Besuchern sind um 16:00 Uhr die meisten Menschen im Zoo.</popup>
b) Wann ist die Besucherzahl am geringsten?
<popup name="Tipp 1">Bei dieser Aufgabe ist es wichtig, sich den Definitionsbereich noch einmal genauer anzugucken. Du darfst auch mit der Abbildung 5.1 deine Begründung unterstützen.</popup> <popup name="Tipp 2">Warum ist es falsch, an dieser Stelle nach der Minimalstelle zu suchen?</popup> <popup name="Lösung">Die Besucherzahl ist um 19:30 Uhr am geringsten. Das ist der einzige Nullpunkt im Definitionsbereich. Die Minimalstelle liegt, wie man in der Abbildung deutlich erkennen kann unterhalb der x-Achse und eine negative Besucherzahl ist nicht möglich. Außerdem liegt diese Stelle nicht mehr im Definitionsbereich.</popup>
c) Zu welcher Uhrzeit ist der Andrang in den Zoo am größten?
<popup name="Tipp 1">Mit der Frage nach dem größten Andrang ist der größte Zuwachs an Besuchern gemeint.</popup> <popup name="Tipp 2">Der größte Zuwachs an Besuchern entspricht dem Maximum der ersten Ableitung.</popup> <popup name="Lösung">Indem die zweite Ableitung gleich 0 gesetzt wird, kann man die Wendestelle ausrechnen. Daraus ergibt sich t = 12. Da die dritte Ableitung konstant b´(t) = - 0,3 ist, wird auch das hinreichende Kriterium erfüllt. Also sind die meisten Menschen um 12:00 Uhr auf den Weg in den Zoo.</popup>}}

Aufgabe 6: Forderaufgabe: Ausblick auf die Integralrechnung

Aufgabe 6 : Die Autofahrt

{{{2}}}