Benutzer:L.hodankov/Quadratische Funktionen/Anwendungen
Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule https://projekte.zum.de/wiki/Benutzer:Buss-Haskert/Quadratische_Funktionen. Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA.
Herzlichen Dank!
SEITE IM AUFBAU
1 Quadratische Funktionen entdecken
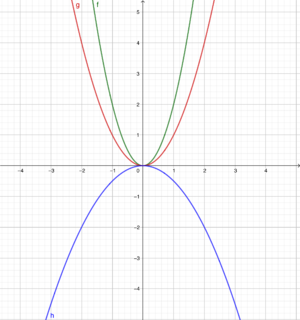
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
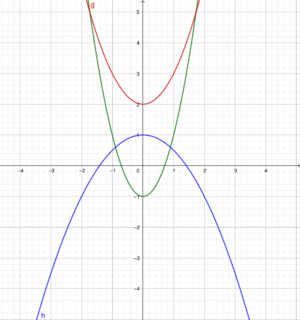
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
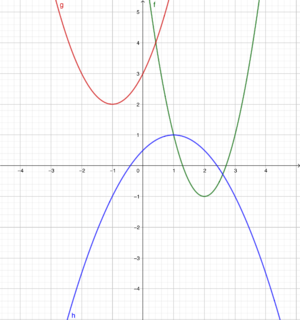
5 Die Scheitelpunktform quadratischer Funktionen f(x) = a(x+d)² + e
6 Die Normalform f(x) = x² + px + q und die allgemeine Form quadratischer Funktionen f(x) = ax² + bx + c
7 Nullstellen quadratischer Funktionen
4 Modellieren - Anwendungsaufgaben
In unserer Umgebung gibt es viele Beispiele für Parabeln. Besonders häufig sind sie z.B. beim Brückenbau und bei Wurf- bzw. Flugbahnen zu sehen.
Es gibt besondere Punkte, die in Anwendungen immer wieder von Bedeutung sind:
- Scheitelpunkt
- Nullstellen
- Schnittpunkt mit der y-Achse
- Koordinaten eines beliebigen Punktes
Wenn in Anwendungsaufgaben die Funktionsgleichung gegeben ist, schau, welche Form sie hat, zeichne eine passende Skizze, beschrifte die Achsen und trage gegebene Punkte ein.
(Autor:Roulex 45; https://de.wikipedia.org/wiki/Golden_Gate_Bridge#/media/Datei:Golden-Gate-Bridge.svg)
Mögliche Fragen sind:
- Wie hoch verläuft die Fahrbahn über dem Meeresspielgel? (Scheitelpunkt, y-Koordinate)
- Wie lang sind die Hängeseile? (Koordinaten bestimmter Punkte auf der Parabel)
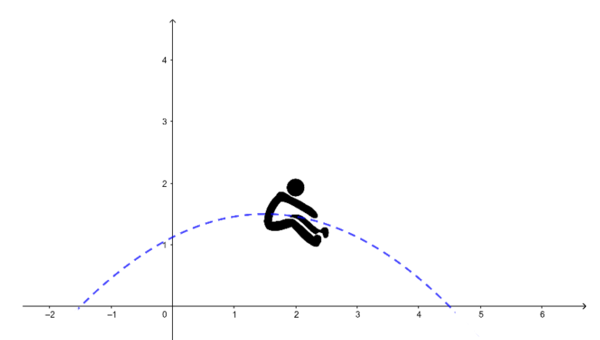
Mögliche Fragen sind:
- Wie weit springt die Person? (2. Nullstelle)
- Wann hat sie die größte Sprunghöhe erreicht? (x-Koordinate des Scheitelpunktes)
- Wie hoch ist die größte Höhe des Körperschwerpunktes? (y-Koordinate des Scheitelpunktes)
- Wie hoch liegt der Körperschwerpunkt beim Absprung über dem Boden? (Schnittpunkt mit der y-Achse)
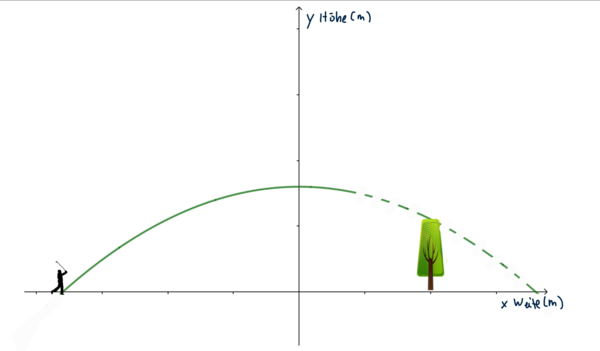
Mögliche Fragen sind:
- Wie weit fliegt der Ball? (Abstand zwischen den Nullstellen)
- Wie hoch ist die maximale Höhe des Balls? (y-Koordinate des Scheitelpunktes)
- Wird der Baum überspielt oder landet der Ball im Baum? (Vergleiche die y-Koordinate des des Punktes P(xBaum|y) mit der Höhe des Baumes)