Seite im Aufbau
Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.
Schätzfrage
Wie viel Flüssigkeit passt in das Trinkpäckchen? Schätze.
Welche Volumeneinheiten hast du bei der Beantwortung der Frage genutzt? Welche Volumeneinheiten kennst du?
Einheiten für den Rauminhalt (das Volumen) sind:
Liter (l); Milliliter (ml) oder
m³, dm³, cm³
4 Volumeneinheiten
Um das Volumen des Trinkpäckchens (des Quaders) berechnen zu können, müssen wir also mit Volumeneinheiten umgehen können.
Als Volumeneinheiten verwenden wir Würfel mit der Kantenlänge 1 m oder 1 cm oder ...
Hier einige Beispiele für deine Vorstellung:

1 Stecknadelkopf hat ungefähr den Rauminhalt 1 mm³

1 Zuckerwürfel hat ungefähr den Rauminhalt 1cm³

1 Milchkarton hat den Rauminhalt 1 dm³ (= 1 Liter)
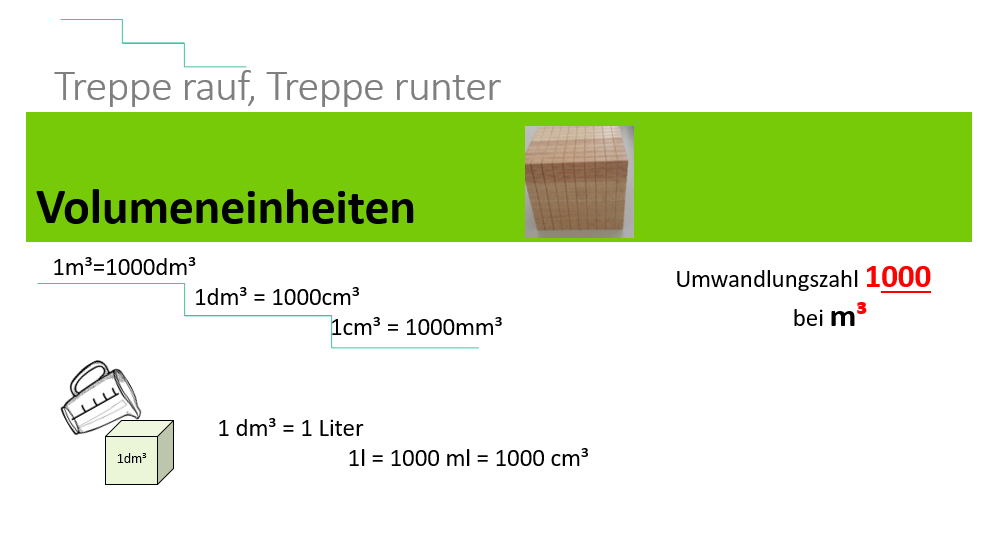
Volumeneinheiten
Der Rauminhalt eines Körpers (auch Volumen genannt) gibt die Größe des Körpers an. Um den Rauminhalt vergleichen zu können, geben wir ihn in Würfeln als Volumeneinheit an.
Ein Würfel mit der Kantenlänge 1cm hat das Volumen von 1cm³ (gesprochen 1 Kubikzentimeter).
Erinnerung: engl. 'cube' heißt 'Würfel'.
Volumeneinheiten umrechnen
Wie viele cm³ Würfel passen in 1 dm³?
Schätze. Schau dir anschließend die Bilderfolge an und erkläre!

Einheit Liter
Bei Flüssigkeiten verwenden wir für das Volumen auch die Einheit Liter.
1 Liter (l) = 1dm³;
1 Milliliter (ml) = 1cm³

Volumeneinheiten
Übertrage die Einheitentreppe für die Volumeneinheiten in dein Heft.
Übung 1: Volumeneinheiten zuordnen
Ordne in den Körpern die passenden Rauminhalte zu.
Übung 2: Volumeneinheiten umwandeln
Wie viele Kubikzenitmeter sind 2 Kubikdezimeter?
2 dm³ = 2 · 1000 cm³ = 2000 cm³
Wie viele Kubikmeter sind 54 000 000 Kubikzentimeter?
54 000 000 cm³ = 54 000 dm³ = 54 m³
Übung 3
Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und gib in der geforderten Einheit an.
- S. 90 Nr. 3
- S. 90 Nr. 6
- S. 90 Nr. 7
Volumenangaben in Kommaschreibweise
Ist das Volumen in Kommaschreibweise gegeben, hilft dir die Stellenwerttafel bei der Umwandlung.
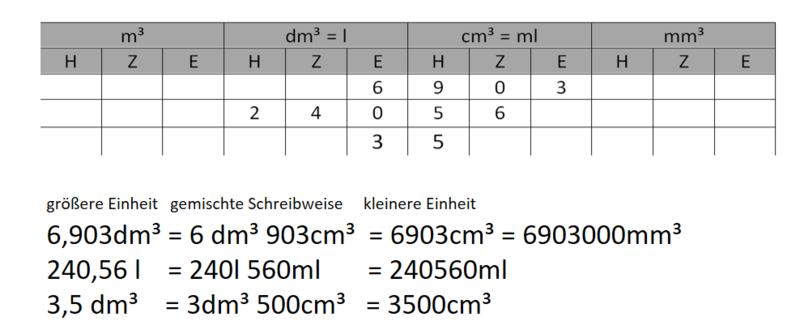
Übertrage die Beispiele in dein Heft.
Übung 4: Volumeneinheiten in der Kommaschreibweise
Bearbeite die nachfolgenden LearningApps. Gib das Volumen in drei Schreibweisen an. Tipp: Denke an die Einheitentabelle
Übung 5
Löse die Aufgaben aus dem Buch. Die Einheitentabelle kann dir helfen.
- S. 90 Nr. 8
- S. 91 Nr. 9
- S. 91 Nr. 11
Vermischte Übungen
Die nachfolgenden Apps und Applets bieten dir weitere Übungsmöglichkeiten.
Applet von S. Ripp
Applet von S. Ripp
realmath Level 1
realmath Level 2
realmath Level 3a
realmath Level 3b
realmath Level 4














