Herta-Lebenstein-Realschule/Lernpfad Brüche/Erweitern und Kürzen

zurück zur Seite der Herta-Lebenstein-Realschule

0 Vorwissen

1 Brüche und gemischte Zahlen
2 Brüche am Zahlenstrahl
3 Brüche erweitern und kürzen
4 Brüche vergleichen und ordnen

5 Brüche und Prozent

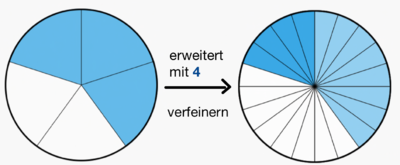
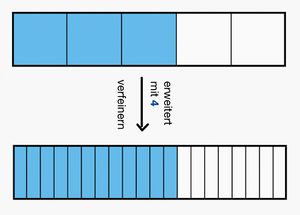
3 Verschiedene Brüche mit gleichem Wert - Brüche erweitern und kürzen

Einstieg-Brüche falten

Zeichne auf einem Blatt Papier ein Quadrat und schneide es aus. Markiere (Schraffiere) dann die Hälfte des Quadrates mit einer beliebigen Farbe. Besprich dich mit deinem Partner, wie ihr den entstandenen Bruch nun nennen würdet. Faltet das Quadrat nun weitere Male und besprecht, wie die entstandenen Brüche heißen.

Übung 1 (im online-Brüche-Buch)

Lies dir die Seiten 30 - 34 im unten stehenden Link durch und bearbeite die entsprechenden Aufgaben
https://www.alice.edu.tum.de/bruchrechnen.html#/30

• Nr. 33 - 37

Hefteintrag: Erweitern und Kürzen

Beim Erweitern eines Bruches werden Zähler und Nenner mit derselben Zahl multipliziert. Die Einteilung wird feiner.

      $\frac{3}{5}$          =        $\frac{3\cdot4}{5\cdot4}$        =        $\frac{12}{20}$

Bruch und erweiterter Bruch haben denselben Wert.

Beim Kürzen eines Bruches werden Zähler und Nenner durch dieselbe Zahl dividiert. Die Einteilung wird gröber.

    $\frac{15}{20}$    =                $\frac{15:5}{20:5}$        =        $\frac{3}{4}$

Bruch und gekürzter Bruch haben denselben Wert.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 2

Kontrolliere mit der folgenden App, ob du die Grundlagen des Erweiterns und Kürzens verstanden hast. Spiele gegen deinen Partner. Wenn du keinen hast, spiele gegen den Computer. Mal sehen, wer das schnellere Pferd hat.

Übung 3

Festige dein Wissen, indem Du auf den untenstehenden Link klickst und die Aufgaben auf den Seiten 35 - 38 bearbeitest.
https://www.alice.edu.tum.de/bruchrechnen.html#/35

• Nr. 38 - 53

Übung 4

Bearbeite die Aufgaben aus dem Buch. Notiere deine Lösungen übersichtlich im Heft.

• S. 43 Nr. 4c,d
• S. 43 Nr. 5

Nr. 4
c) $\frac{2}{100}$; $\frac{30}{100}$; $\frac{35}{100}$; $\frac{36}{100}$; $\frac{80}{100}$; $\frac{75}{100}$; $\frac{250}{100}$

d) $\frac{6}{1000}$; $\frac{44}{1000}$; $\frac{64}{1000}$; $\frac{48}{1000}$; $\frac{45}{1000}$

Nr. 5
a) $\frac{1}{2}$ = $\frac{6}{12}$

b) $\frac{4}{5}$ = $\frac{32}{40}$

c) $\frac{5}{9}$ = $\frac{35}{63}$

d) $\frac{3}{7}$ = $\frac{18}{42}$

e) $\frac{5}{9}$ = $\frac{60}{108}$

f) $\frac{8}{11}$ = $\frac{88}{121}$

g) $\frac{1}{3}$ = $\frac{9}{27}$

h) $\frac{2}{7}$ = $\frac{16}{56}$

i) $\frac{5}{8}$ = $\frac{45}{72}$

j) $\frac{7}{10}$ = $\frac{91}{130}$

k) $\frac{5}{12}$ = $\frac{60}{144}$

l) $\frac{9}{13}$ = $\frac{99}{143}$

Übung 5 - Erweitere auf einen gemeinsamen Nenner

Arbeite zunächst im online-Brüche-Buch. Bearbeite anschließend die Aufgabe aus dem Buch.

• Aufgabe 50
• S. 43 Nr. 6

a) $\tfrac{1}{3}$ und $\tfrac{1}{4}$ Der (kleinste) gemeinsame Nenner ist 12. Erweitere!
$\tfrac{4}{12}$ und $\tfrac{3}{12}$
b) $\tfrac{5}{6}$ und $\tfrac{4}{9}$ Der (kleinste) gemeinsame Nenner ist 18. Erweitere!
$\tfrac{15}{18}$ und $\tfrac{8}{18}$

Löse die anderen Aufgaben ebenso.

Übung 6

Bearbeite die Aufgaben aus dem Buch. Notiere deine Lösungen übersichtlich im Heft.

• S. 43 Nr. 7c,d
• S. 43 Nr. 8

Nr. 7

c) $\frac{1}{3}$; $\frac{2}{3}$; $\frac{3}{5}$; $\frac{4}{7}$; $\frac{5}{9}$

d) $\frac{2}{7}$; $\frac{4}{5}$; $\frac{3}{8}$; $\frac{7}{11}$; $\frac{9}{13}$

Nr. 8

a) mit 3; mit 2; mit 8

b) mit 5; mit 7; mit 8

Übung 7 - Würfelspiel (Partnerarbeit)

Nehmt euch zu zweit drei Würfel. Spielt damit das Spiel

• S. 44 Nr. 10

Räumt anschließend die Würfel wieder zurück.

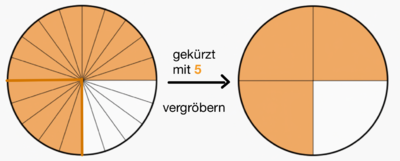
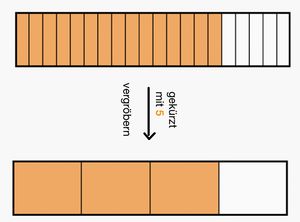
Vollständiges Kürzen

Du kannst Brüche oft mehrmals kürzen. Der Bruch ist vollständig gekürzt, wenn Zähler und Nenner keine gemeinsamen Teiler mehr haben.

$\frac{48}{72} = \frac{12}{18} = \frac{4}{6} = \frac{2}{3}$

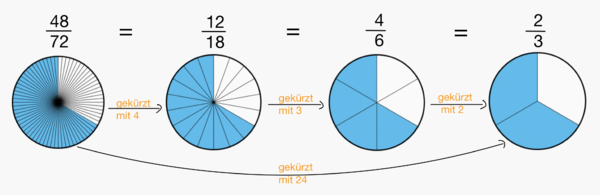
Zuerst wurde der Bruch mit 4 gekürzt, dann mit 3 und letztlich nochmal mit 2. Um sofort mit dem größten gemeinsam Teiler zu kürzen, kannst Du auch die Teilermengen notieren (siehe grüner Kasten auf der Buchseite 44).
T₄₈=$\{$1;2;3;4;6;8;12;16;24;48$\}$
T₇₂=$\{$1;2;3;4;6;8;9;12;18;24;36;72$\}$.
Der größte gemeinsame Teiler von 48 und 72 ist also 24, ggt(48,72) = 24.
Du kannst also direkt mit 24 kürzen.

Vollständiges Kürzen

Lies das Beispiel oben durch. Fülle anschließend den Lückentext unten aus. Übertrage ihn in dein Heft.

Brüche lassen sich häufig mehrmals kürzen.
$\frac{15}{45}$ = $\frac{5}{15}$ = $\frac{1}{3}$. Wie Du siehst gehören die Kürzungszahlen 3 und 5 zur Teilermenge des Zählers und Nenners. Stellst Du nun die Teilermenge auf, kannst Du sofort den größten gemeinsamen Teiler finden.
T₁₅ = {1; 3; 5; 15}
T₄₅ = {1; 3; 5; 15; 45} Also ist 15 der als ggT (größter gemeinsamer Teiler) zu bezeichnen. Folglich kannst Du auch sofort mit 15 kürzen:
$\frac{15}{45}$ = $\frac{1}{3}$

Der Bruch ist sofort vollständig gekürzt

Übung 8

Bearbeite nun folgende Learningapps.

Übung 9

Bearbeite die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und kürze vollständig.

• S. 44 Nr. 12
• S. 44 Nr. 13
• S. 44 Nr. 14
• S. 44 Nr. 18

Nr. 12
a) $\frac{42}{48}$ = $\frac{7}{8}$ (ggT: 6)

b) $\frac{90}{120}$ = $\frac{3}{4}$ (ggT: 30)

c) $\frac{54}{90}$ = $\frac{3}{5}$ (ggT: 18)

d) $\frac{40}{56}$ = $\frac{5}{7}$ (ggT: 8)

e) $\frac{72}{108}$ = $\frac{2}{3}$ (ggT: 36)

f) $\frac{60}{135}$ = $\frac{4}{9}$ (ggT: 15)

g) $\frac{48}{144}$ = $\frac{1}{3}$ (ggT: 48)

h) $\frac{54}{243}$ = $\frac{2}{9}$ (ggT: 27)

Nr. 13
a) gleich
b) gleich
c) ungleich
d) ungleich
e) ungleich
f) ungleich
g) ungleich

h) ungleich

Sucht zuerst den größten gemeinsamen Teiler.

Nr. 14
a) $\frac{8}{16}$ = $\frac{1}{2}$

b) $\frac{25}{75}$ = $\frac{1}{3}$

c) $\frac{12}{18}$ = $\frac{2}{3}$

d) $\frac{24}{64}$ = $\frac{3}{8}$

e) $\frac{36}{90}$ = $\frac{2}{5}$

f) $\frac{32}{128}$ = $\frac{1}{4}$

g) $\frac{48}{144}$ = $\frac{1}{3}$

h) $\frac{56}{140}$ = $\frac{2}{5}$

4 Brüche vergleichen und ordnen