Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel

Seite im Aufbau

zurück zur Seite der Herta-Lebenstein-Realschule

Startseite Flächeninhalt und Rauminhalt

1 Flächen
2 Umfang und Flächeninhalt von Rechtecken
3 Oberfläche von Quader und Würfel
4 Rauminhalt (Volumen)
5 Rauminhalt (Volumen) von Quader und Würfel

5 Rauminhalt (Volumen) von Quader und Würfel

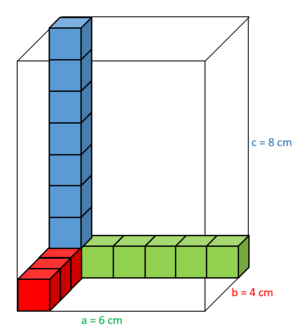
Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.

Schätzfrage

Wie viel Flüssigkeit passt in das Trinkpäckchen?

Wie viele Kubikzentimeterwürfel passen hinein?

Schätze.

Um deine Schätzung zu prüfen, lege das Päckchen mit kleinen Kubikzentimeterwürfeln aus:

Es passen 6 Würfel in eine Reihe.
Es passen 4 Reihen in den Boden.
Es passen ca. 8 Schichten übereinander.

Nutze das nachfolgende GeoGebra-Applet, um herauszufinden, wie du mit diesen Angaben das Volumen des Trinkpäckchens berechnen kannst:

Applet von Matthias Hornof Originallink: https://www.geogebra.org/m/EcHrrMaC

Rauminhalt (Volumen) eines Quaders

Den Rauminhalt (das Volumen) berechnen wir mit der Formel:  

V = Länge ∙ Breite ∙ Höhe
    =  a ∙ b ∙ c

Beim Würfel rechnen wir also:
V = Länge ∙ Breite ∙ Höhe
    =  a ∙ a ∙ a
    = a³

Das Volumen des Trinkpäckchens beträgt also
V = a ∙ b ∙ c
    =  6 ∙ 4 ∙ 8

    = 192 (cm³)

Da die Höhe des Trinkpäckchens etwas höher als 8 cm ist (nämlich 8,5cm), beträgt das tatsächliche Volumen 204 cm³, also ist die Inhaltsangabe von 200 ml richtig.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1

Löse auf der Seite realmath so viele Aufgaben, bis du mindestens 300 Punkte gesammelt hast.
Tipp: Du kannst durch Ziehen an den Punkten den Quader mit Kubikzentimeterwürfeln ausfüllen.

• Übung realmath (Quader)
• Übung realmath (Würfel)

Übung 2

Löse die Aufgaben aus dem Buch. Achte auf eine übersichtliche Darstellung. Schreibe die Kantenlängen des Quaders auf. Notiere die Formel, setze die Werte ein und berechne. Denke an die passende Einheit.

• S. 93 Nr. 5
• S. 93 Nr. 4

Stelle die Schieberegler passend zur Aufgabe ein und kontrolliere deine Rechnung.
Originallink: https://www.geogebra.org/m/ytgp88hk

Übung 3 Nachdenkaufgabe

Wie ändert sich das Volumen eines Würfels, wenn man die Kantenlängen verdoppelt?

Stelle eine Vermutung auf und überprüfe sie an einem Beispiel bzw. nutze das Applet unten.

Übung 4 Kantenlänge eines Quaders berechnen

Du kannst bei gegebenem Volumen auch eine fehlende Kantenlänge berechnen. Nutze dazu die Umkehraufgabe.
geg: V = 60 cm³; a = 5 cm; b = 3 cm
ges: c
V = a ∙ b ∙ c   |Werte einsetzen
60 = 5 ∙ 3 ∙ c
60 = 15 ∙ c   |:15 Umkehraufgabe 60 : 15 = c
60 : 15 = c
4 (cm) = c

• S. 93 Nr. 6 b, c, d
• S. 95 Nr. 15

Stelle die Schieberegler passend zur Aufgabe ein und kontrolliere deine Rechnung.
Originallink: https://www.geogebra.org/m/ytgp88hk

Anwendungsaufgaben

Um Anwendungsaufgaben lösen zu können, musst du die Begriffe "Oberfläche und Volumen" verstanden haben.
Prüfe dein Wissen, indem du den Situationen den passenden Begriff zuordnest.

Übung 5 Anwendungsaufgaben

Löse die Aufgaben aus dem Buch. Notiere zunächst, welche Größen gegeben und welche gesucht sind. Eine Skizze hilft dir.

• S. 95 Nr. 17
• S. 95 Nr. 18
• S. 93 Nr. 3
• S. 93 Nr. 7

Vermischte Übungen - online

Bearbeite die Aufgaben auf der Seite Aufgabenfuchs zur Berechnung des Volumens und der Oberfläche von Quader und Würfel.