Herta-Lebenstein-Realschule/Lernpfad Brüche/Brüche

zurück zur Seite der Herta-Lebenstein-Realschule

0 Vorwissen

1 Brüche und gemischte Zahlen
2 Brüche am Zahlenstrahl
3 Brüche erweitern und kürzen
4 Brüche vergleichen und ordnen

5 Brüche und Prozent

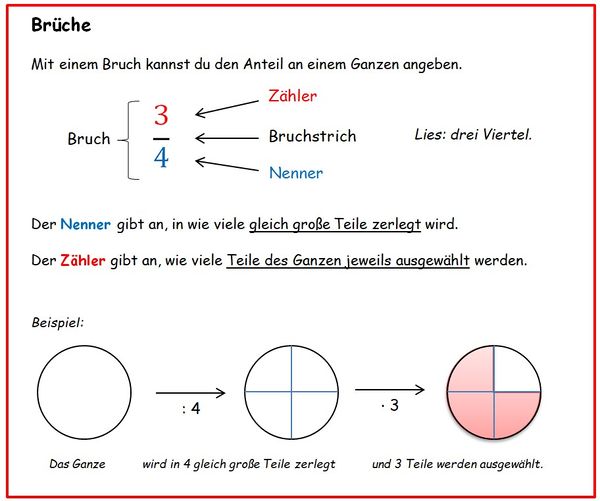
1 Einführung in das Thema Brüche

Merke: Brüche

Applet von Jens Werbing (Originallink: https://www.geogebra.org/m/bbmcTJbh)

Bruch als Division

Ein Bruch ist mit einer Division gleichzusetzen. Z.B.: $\frac{2}{3}$ = 2 : 3
Dabei gibt der Zähler die Anteile der Bruchteile an, in diesem Fall 2.
Der Bruchstrich steht für das Divisionszeichen

Der Nenner gibt an, in wie viele Teile das Ganze unterteilt ist, hier 3.

Die Videos veranschaulichen dies noch einma:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1 - Brüche am Geobrett

Bearbeite die nachfolgenden Übungen am Geobrett. Nimm dazu ein Geobrett aus dem Schrank und spanne die Gummis, wie im Applet vorgegeben.

direkter Link: https://www.geogebra.org/m/tsuyj68c

Applet von FLINK Team

https://www.geogebra.org/m/ybfytbvu direktert Link

Applet von FLINK Team GeoGebra - Buch zu Brüchen https://www.geogebra.org/m/pge8d4x3 (FLINK Team)

Übung 2 (Buch)

Löse die Aufgaben aus dem Buch

• S. 38 Nr. 3
• S. 38 Nr. 5
• S. 38 Nr. 6
• S. 38 Nr. 9
• S. 38 Nr. 11

Nr. 3
a) $\frac{2}{5}$
b) $\frac{3}{4}$
c) $\frac{2}{8}$
d) $\frac{5}{6}$
e) $\frac{7}{15}$
f) $\frac{3}{5}$

Nr. 5
a) $\frac{2}{6}$
b) $\frac{8}{12}$
c) $\frac{8}{15}$

Nr. 6
a) zu Fuß $\frac{11}{28}$
mit der Bahn $\frac{17}{28}$

b) weiße $\frac{10}{30}$
blaue $\frac{20}{30}$

c) Ananassaft: $\frac{1}{6}$
Apfelsaft: $\frac{2}{6}$
Orangensaft: $\frac{3}{6}$

Lösungen zu Nr. 9

Mach dir vor der Zeichnung des Rechtecks Gedanken über die Aufteilung. Der Nenner ist hierfür ausschlaggebend. Die Anzahl an Zentimetern oder Kästchen, die du wählst, sollte durch diese Zahl teilbar sein.

Übung 3 (im online-Brüche-Buch)

Bearbeite im Folgenden die Aufgaben des folgenden Internetlinks https://www.alice.edu.tum.de/bruchrechnen.html#/10nks bis Seite 14 einschließlich.

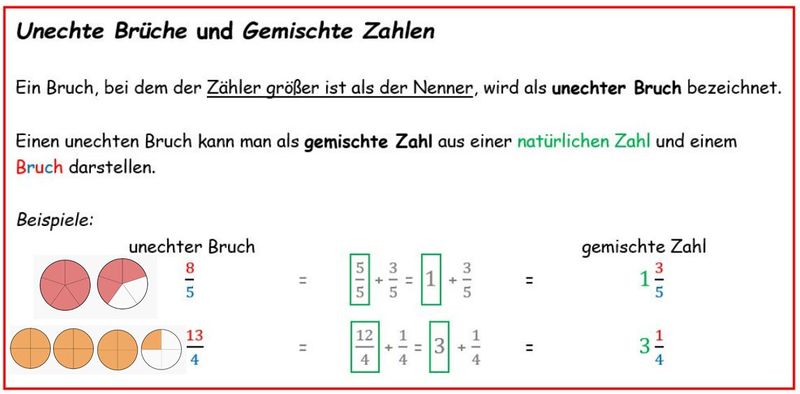
Gemischte Zahlen

Einstieg - Mehr als ein Ganzes

Bearbeite im Buch die Einstiegsaufgabe oben auf Seite 39.

Es gibt zwei Möglichkeiten den Bruch darzustellen. Einmal als unechten Bruch und einmal als gemischte Zahl

Alternativ:

Merke: Unechte Brüche und Gemischte Zahlen

Umwandlung

Schau Dir nun das folgende Video an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 4: Mehr als ein Ganzes

Bearbeite die Aufgaben auf der Seite realmath. Schau die Abbildungen an und ergänze die Lücken. Erkläre deinem Partner/deiner Partnerin, wie du vorgehst.

• gemischte Zahl
• unechter Bruch
• gemischte Zahl - unechter Bruch

Übung 5 (im online-Brüche-Buch)

Festige dein Wissen, indem du auf den untenstehenden Link klickst und die Aufgaben auf den Seiten 51 - 54 bearbeitest.

https://www.alice.edu.tum.de/bruchrechnen.html#/10nks

Übung 6 (Buch)

Bearbeite nun die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und wandle um.

• S. 39 Nr. 1
• S. 39 Nr. 2

Übung 7 (Partnerarbeit)

Lies dir den Lerntipp auf der Seite 39 durch und erkläre ihn deinem Partner.

Bearbeite im Anschluss die Aufgaben 3 und 4 auf der Seite. Du darfst rechnen wie im Beispiel oder aber wie Petra im Lerntipp

Übung 8 (Buch)

Bearbeite nun die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und wandle um.

• S. 39 Nr. 5

Wandle die gemischte Zahl zuerst in einen unechten Bruch um und ergänze dann die fehlende Zahl. Bei den Aufgaben d-f musst du zudem beachten, dass die Nenner auf beiden Seiten gleich sind.

Überprüfe dein Wissen abschließend mit den folgenden Learningapps.

2 Brüche am Zahlenstrahl