Benutzer:Buss-Haskert/Flächeninhalt und Rauminhalt/Rauminhalt von Quader und Würfel: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 20: | Zeile 20: | ||
[[Datei:Trinkpäckchen 2.jpg|rahmenlos]] Es passen 6 Würfel in eine Reihe. <br> | [[Datei:Trinkpäckchen 2.jpg|rahmenlos]] Es passen 6 Würfel in eine Reihe. <br> | ||
[[Datei:Trinkpäckchen 3.jpg|rahmenlos]] Es passen 4 Reihen in den Boden. <br> | [[Datei:Trinkpäckchen 3.jpg|rahmenlos]] Es passen 4 Reihen in den Boden. <br> | ||
[[Datei:Trinkpäckchen 4.jpg|rahmenlos]] Es passen 8 | [[Datei:Trinkpäckchen 4.jpg|rahmenlos]] Es passen ca. 8 Schichten übereinander. | ||
| Zeile 27: | Zeile 27: | ||
<small>Applet von Matthias Hornof</small> <br> | <small>Applet von Matthias Hornof</small> <br> | ||
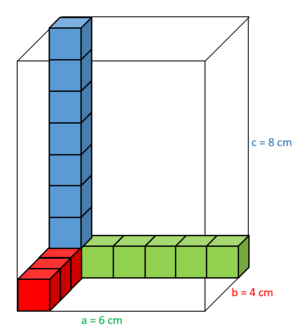
{{Box|1=Rauminhalt (Volumen) eines Quaders|2=Den Rauminhalt (das Volumen) berechnen wir mit der Formel: <br> | {{Box|1=Rauminhalt (Volumen) eines Quaders|2=[[Datei:Volumen Quader Würfel eingezeichnet.png|rechts|rahmenlos]]Den Rauminhalt (das Volumen) berechnen wir mit der Formel: <br> | ||
V = Länge ∙ Breite ∙ Höhe <br> | V = Länge ∙ Breite ∙ Höhe <br> | ||
= a ∙ b ∙ c |3=Arbeitsmethode}} | = a ∙ b ∙ c <br> | ||
<br> | |||
Das Volumen des Trinkpäckchens beträgt also <br> | |||
V = a ∙ b ∙ c <br> | |||
= 6 ∙ 4 ∙ 8 <br> | |||
= 192 (cm³) <br> | |||
|3=Arbeitsmethode}} | |||
Da die Höhe des Trinkpäckchens etwas höher als 8 cm ist (nämlich 8,5cm), beträgt das tatsächliche Volumen 204 cm³, also ist die Inhaltsangabe von 200 ml richtig. | |||
<br> | <br> | ||
<div class="grid"> | <div class="grid"> | ||
Version vom 7. Januar 2022, 15:48 Uhr
Seite im Aufbau
1 Flächen
2 Umfang und Flächeninhalt von Rechtecken
3 Oberfläche von Quader und Würfel
4 Rauminhalt (Volumen)
5 Rauminhalt (Volumen) von Quader und Würfel
5 Rauminhalt (Volumen) von Quader und Würfel
Für unser Picknick im Schwimmbad packen wir auch ein Getränk (Trinkpäckchen) ein.
Um deine Schätzung zu prüfen, lege das Päckchen mit kleinen Kubikzentimeterwürfeln aus:
Es passen 6 Würfel in eine Reihe.
Es passen 4 Reihen in den Boden.
Es passen ca. 8 Schichten übereinander.
Nutze das nachfolgende GeoGebra-Applet, um herauszufinden, wie du mit diesen Angaben das Volumen des Trinkpäckchens berechnen kannst:
Applet von Matthias Hornof
Da die Höhe des Trinkpäckchens etwas höher als 8 cm ist (nämlich 8,5cm), beträgt das tatsächliche Volumen 204 cm³, also ist die Inhaltsangabe von 200 ml richtig.
