Benutzer:Buss-Haskert/Prismen/Prismen erkennen: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
K (Rechtschreibung)
Markierung: 2017-Quelltext-Bearbeitung
Zeile 22: Zeile 22:
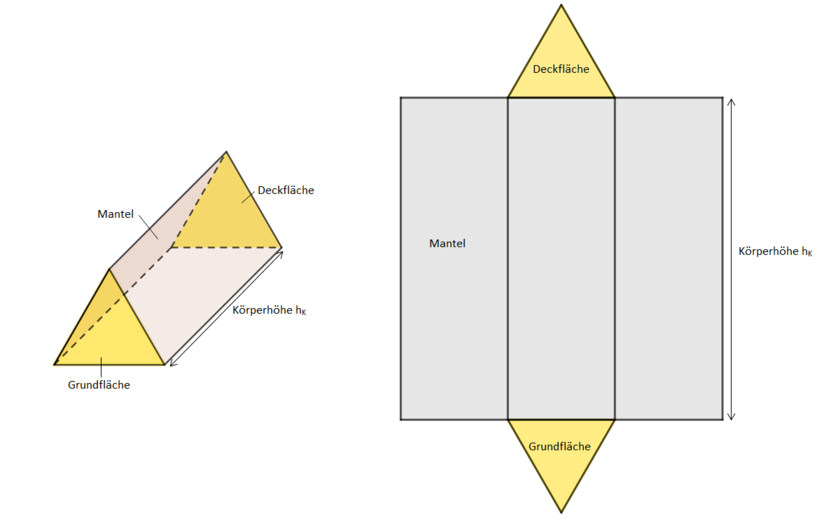
{{Box|Bezeichnungen am Prisma|Ein Prisma setzt sich zusammen aus drei Flächen:<br>
{{Box|Bezeichnungen am Prisma|Ein Prisma setzt sich zusammen aus drei Flächen:<br>
* Die Grundfläche und Deckfläche sind parallel und kongruent (deckungsgleich). Ihre Form bestimmt den Namen des Prismas: Dreickesprisma, Trapezprisma,...<br>
* Die Grundfläche und Deckfläche sind parallel und kongruent (deckungsgleich). Ihre Form bestimmt den Namen des Prismas: Dreickesprisma, Trapezprisma,...<br>
* Die Mantelfläche bsteht aus Rechtecken.<br>
* Die Mantelfläche besteht aus Rechtecken.<br>
* Der Abstand zwischen Grund- und Deckfläche ist die Körperhöhe h<small>K</small> des Prismas.|Arbeitsmethode}}  
* Der Abstand zwischen Grund- und Deckfläche ist die Körperhöhe h<small>K</small> des Prismas.|Arbeitsmethode}}  
[[Datei:Begriffe Prisma.png|rahmenlos|831x831px]]<br>
[[Datei:Begriffe Prisma.png|rahmenlos|831x831px]]<br>

Version vom 16. Mai 2021, 13:45 Uhr

zurück zur Seite der Herta-Lebenstein-Realschule


SEITE IM AUFBAU

1 Prismen erkennen


Was ist ein Prisma?
Teilt man einen Quader mit Schnitten senkrecht zur Grundfläche, entstehen mehrere Teilkörper. Die so entstandenen Körper heißen Prismen (Prisma).

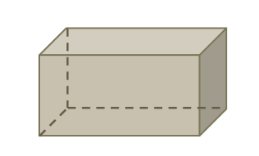
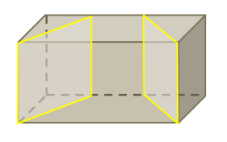
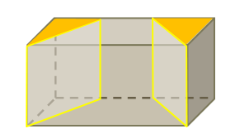
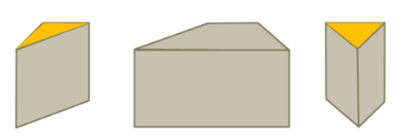
Beispiel:  Zwei Schnitte senkrecht zur Grundfläche. Es entstehen drei Teilkörper.

Entstehung Prisma Bild 1.png
Entstehung Prisma Bild 2.png
Entstehung Prisma Bild 3.png
Entstehung Prisma Bild 5.png



Bezeichnungen am Prisma

Ein Prisma setzt sich zusammen aus drei Flächen:

  • Die Grundfläche und Deckfläche sind parallel und kongruent (deckungsgleich). Ihre Form bestimmt den Namen des Prismas: Dreickesprisma, Trapezprisma,...
  • Die Mantelfläche besteht aus Rechtecken.
  • Der Abstand zwischen Grund- und Deckfläche ist die Körperhöhe hK des Prismas.

Begriffe Prisma.png

Im nachfolgenden GeoGebra-Applet kannst du Prismen mit regelmäßigen n-Ecken als Grund- und Deckfläche darstellen.
Wähle z.B. ein Dreiecksprisma, ein Fünfecksprisma oder ein Siebenecksprisma . Auch die Höhe des Prismas kannst du verändern. Probiere aus.

GeoGebra


GeoGebra

Applet von Hegius


GeoGebra

Applet von holo2012

GeoGebra

Applet von K. Maier


Übung 1 - Verpackungen
Bring zur nächsten Stunde Verpackungen (z.B. von Süßigkeiten) mit zum Matheunterricht. Wir werden dann entscheiden, welche Verpackungen Prismen sind und welche nicht.


Übung 2
Bearbeite die nachfolgenden LearningApps.



Übung 3

Löse die Aufgabe aus dem Buch. Erstelle dazu zu Aufgabenteil a, b und c ein Kantenmodell zum Prisma.
Material: Holzspieße und Erbsen.

  • S. 147 Nr. 4
Was fällt dir auf?


Kantenmodell Dreiecksprisma.pngKantenmodell Fünfecksprisma.pngKantenmodell Sechsecksprisma.png

S. 147 Nr. 4 Tabelle.png
S. 147 Nr. 4 Lösung.png


Übung 4

Löse auf der Seite Aufgabenfuchs die Aufgaben

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7


Übung 5

Löse die Aufgaben mündlich mit deinem Sitznachbarn.

  • S. 147 Nr. 1
  • S. 147 Nr. 2
  • S. 147 Nr. 3
  • S. 147 Nr. 5
  • S. 147 Nr. 6
  • S. 147 Nr. 7


Zusammenfassung: Vertone ein Video
Das nachfolgende Video zeigt, wie du ein Prisma erkennen kannst. Schreibe einen kurzen Vortrag passend zum Video und präsentiere ihn der Klasse.
Video laden
YouTube


2 Schrägbild eines Prismas
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Prismen/Prismen_erkennen&oldid=49670“