Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisteile: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 42: | Zeile 42: | ||
{{Lösung versteckt|1=Für die Berechnungen der Flächeninhalte der Kreisringe hast du immer vom äußeren Kreis den inneren Kreis subtrahiert. Leite so die Formel her:<br> | {{Lösung versteckt|1=Für die Berechnungen der Flächeninhalte der Kreisringe hast du immer vom äußeren Kreis den inneren Kreis subtrahiert. Leite so die Formel her:<br> | ||
A<sub>Kreisring</sub> = A<sub>außen</sub> - A<sub>innen</sub><br> | A<sub>Kreisring</sub> = A<sub>außen</sub> - A<sub>innen</sub><br> | ||
= | = π·r²<sub>a</sub> - π·r²<sub>i</sub> | π als gleichen Faktor ausklammern<br> | ||
= π·( | = π·(r²<sub>a</sub> - r²<sub>i</sub>)|2=Tipp zu b|3=Verbergen}} | ||
{{Box|1=Kreisring|2=Flächeninhalt eines Kreisringes:<br> | {{Box|1=Kreisring|2=Flächeninhalt eines Kreisringes:<br> | ||
A<sub>Kreisring</sub> = π·r<sub>a</sub>² - π·r<sub>i</sub>² | (π als gleichen Faktor ausklammern)<br> | A<sub>Kreisring</sub> = π·r<sub>a</sub>² - π·r<sub>i</sub>² | (π als gleichen Faktor ausklammern)<br> | ||
= π·( | = π·(r²<sub>a</sub> - r²<sub>i</sub>)|3=Arbeitsmethode}}<br> | ||
Die Formel wird veranschaulicht im nachfolgenden Applet:<br> | Die Formel wird veranschaulicht im nachfolgenden Applet:<br> | ||
<ggb_applet id="mdksvgq6" width="1074" height="814" border="888888" /> | <ggb_applet id="mdksvgq6" width="1074" height="814" border="888888" /> | ||
| Zeile 56: | Zeile 56: | ||
* 5 | * 5 | ||
* 23|Üben}} | * 23|Üben}} | ||
{{Box|Übung 3 - Anwendung|Löse die nachfolgende LearningApp.|Üben}} | |||
{{LearningApp|app=ppwg6p33j21|width=100%|height=600px|}} | |||
<br> | |||
=== 3.2 Kreisausschnitt A<sub>S</sub> und Kreisbogen b === | === 3.2 Kreisausschnitt A<sub>S</sub> und Kreisbogen b === | ||
Version vom 9. April 2021, 12:42 Uhr
SEITE IM AUFBAU!!
3 Kreisteile
Welche Arten von Kreisteilen gibt es?
Mache dich mit den verschiedenen Begriffen vertraut:

Applet von GeoGebra Translation Team German, Pöchtrager
3.1 Kreisring
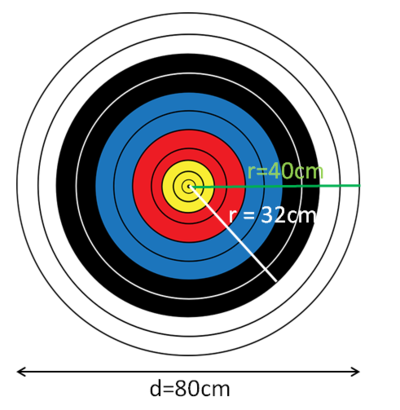
Für die Fläche des weißen Ringes, berechne zunächst den Flächeninhalt der gesamte Scheibe A1 mit dem Radius raußen = 40cm. Subtrahiere anschließend den Flächeninhalt des inneren Kreises A2 mit dem Radius rinnen = 32cm.
AKreisring weiß = A1 - A2
= π·ra² - π·ri²
= π·40² - π·32²
= π·(40² - 32²)
Den Flächeninhalt des schwarzen, blauen und roten Ringes berechne ebenso. Wähle jeweils der Radius des äußeren und inneren Kreises passend:
schwarzer Ring: ra = 32cm; ri = 24cm.
blauer Ring: rra = 24cm; ri = 16cm.
roter Ring: ra = 18cm; ri = 8cm.
Vergleiche deine Lösung zu a)
Aweiß = 1809,56 cm²
Aschwarz = 1407,43 cm²
Ablau = 1005,31 cm²
Arot = 603,19 cm²
Agelb = 201,06 cm²
Für die Berechnungen der Flächeninhalte der Kreisringe hast du immer vom äußeren Kreis den inneren Kreis subtrahiert. Leite so die Formel her:
AKreisring = Aaußen - Ainnen
= π·r²a - π·r²i | π als gleichen Faktor ausklammern
Die Formel wird veranschaulicht im nachfolgenden Applet:

3.2 Kreisausschnitt AS und Kreisbogen b

Applet von IT Wombat
Mittelpunktswinkel und ihre Bezeichnungen
NOCH ERGÄNZEN






