Benutzer:Buss-Haskert/Prismen/Netz und Oberfläche: Unterschied zwischen den Versionen
K (Video und Übungen ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 85: | Zeile 85: | ||
* S. 151 Nr. 2 | * S. 151 Nr. 2 | ||
* S. 152 Nr. 5 |Üben}} | * S. 152 Nr. 5 |Üben}} | ||
{{Lösung versteckt|[[Datei:S. 151 Nr. 2a Tipp.png|rahmenlos|500x500px]]|Tipp zu 2a|Verbergen}} | |||
=== Netze von Prismen zeichnen=== | ===Netze von Prismen zeichnen=== | ||
<br> | <br> | ||
{{#ev:youtube|Q55WTFScX64|800|center}} | {{#ev:youtube|Q55WTFScX64|800|center}} | ||
| Zeile 92: | Zeile 93: | ||
{{Box|Ubung 3|Löse die Aufgabe aus dem Buch. Schau das Video erneut an, wenn du Schwierigkeiten hast. | {{Box|Ubung 3|Löse die Aufgabe aus dem Buch. Schau das Video erneut an, wenn du Schwierigkeiten hast. | ||
* S. 151 Nr. 3|Üben}} | * S. 151 Nr. 3|Üben}} | ||
{{Box|Zusammenfassung: Vertone ein Video|Das nachfolgende Video zeigt, wie du ein Prisma erkennen kannst. Schreibe einen kurzen Vortrag passend zum Video und präsentiere ihn der Klasse.|Meinung}} | {{Box|Zusammenfassung: Vertone ein Video|Das nachfolgende Video zeigt, wie du ein Prisma erkennen kannst. Schreibe einen kurzen Vortrag passend zum Video und präsentiere ihn der Klasse.|Meinung}} | ||
{{#ev:youtube|Wpb8D8sMfSU|800|center|||start=34&end=228}} | {{#ev:youtube|Wpb8D8sMfSU|800|center|||start=34&end=228}} | ||
Version vom 3. April 2021, 18:57 Uhr
SEITE IM AUFBAU
1 Prismen erkennen
2 Schrägbild eines Prismas
3 Netz und Oberfläche
4 Volumen
5 Projekt: Verpackungen gestalten
3 Netz und Oberfläche eines Prismas
In den nachfolgenden GeoGebra-Applets kannst du mit dem Schieberegler die Netze entfalten. Probiere aus!

Applet von R. Schmidt

Applet von K. Maier

Applet von Pöchtrager
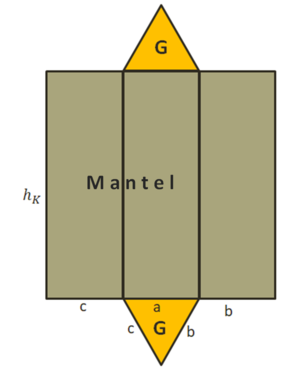
Die Oberfläche setzt sich aus der Grund- und Deckfläche und dem Mantel zusammen.
Die Grund- und Deckfläche sind gleich groß, daher kannst du in der Berechnung 2·G berechnen.
Um den Flächeninhalt für die Grundfläche zu bestimmen, wiederhole die bekannten Flächeninhaltsformeln für Dreiecke und Vierecke. (Du findest die Formeln auch hinten im Schulbegleiter.)
Die Breite des Mantels entspricht der Körperhöhe hK des Prismas.
Die Länge entspricht dem Umfang u der Grundfläche. Erinnerung: Umfang ist drum herum, die Ameise läuft einmal um die Figur herum.
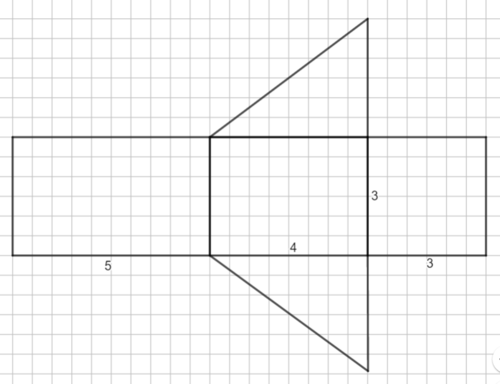
Beispielrechnung zur Bastelvorlage:
O = 2 · G + M
① Berechne G:
G = ADreieck
=
=
= 5,55 (cm²)
② Berechne M:
M = u · hK
= (4+3+4) · 12
= 11 · 12
= 132 (cm²)
③ Berechne O:
O = 2 · G + M
= 2 · 5,55 + 132
= 143,1 (cm²)
Netze von Prismen zeichnen