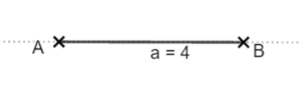Benutzer:Buss-Haskert/Prismen/Schrägbild

zurück zur Seite der Herta-Lebenstein-Realschule

SEITE IM AUFBAU

Prismen - Projekt: Verpackungen gestalten

1 Prismen erkennen
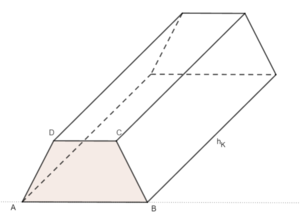
2 Schrägbild eines Prismas
3 Netz und Oberfläche
4 Volumen
5 Projekt: Verpackungen gestalten

2 Schrägbild eines Prismas

Schrägbild eines Dreiecksprismas zeichnen

Zeichne das Schrägbild eines Dreiecksprismas mit den Seiten

a = 3cm; b = 3cm und c = 3cm und der Körperhöhe h_K = 12 cm.

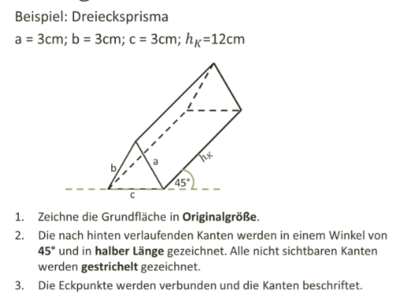
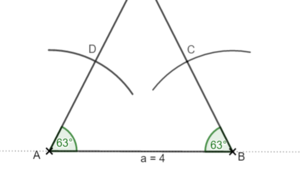
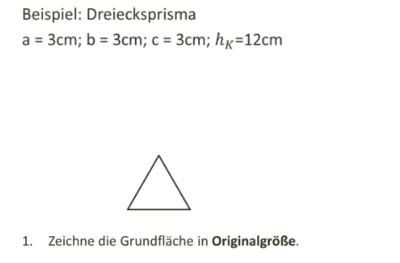
1. Schritt: Zeichne die Grundfläche des Prismas in Originalgröße:
Dreieck ABC mit a = b = c = 3cm.
Erinnerung: Konstruiere das Dreieck mit dem Kongruenzsatz SSS.
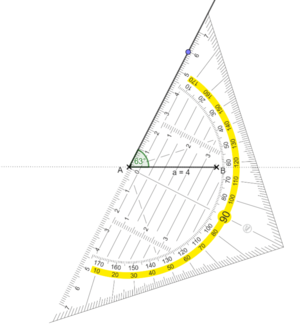
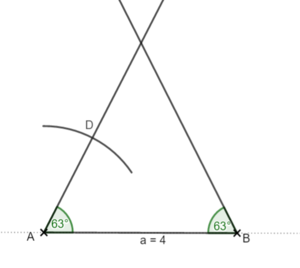
Zeichne zunächst die Strecke c = 3cm mit den Endpunkten A und B. Zeichne dann um A und B einen Kreis mit dem Radius r = a = b = 3cm. Die Kreisbögen schneiden sich im Punkt C. Verbinde A und B mit C.

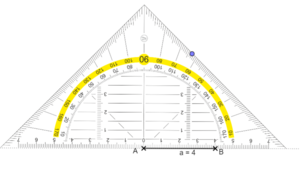
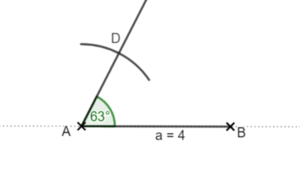
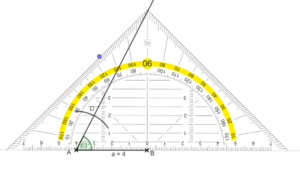
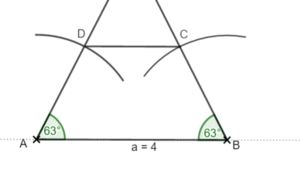
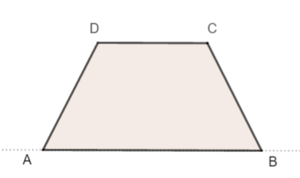
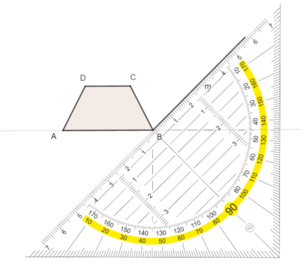
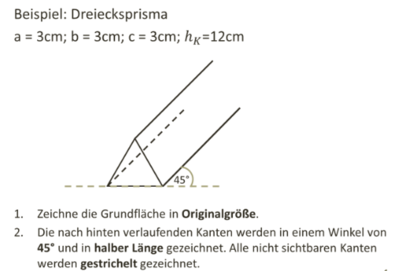
Zeichne nun die nach hinten verlaufenden Kanten in den Eckpunkten der Grundseite mit einem Winkel von 45° schräg nach hinten.
Dabei werden die Kanten nur in halber Länge gezeichnet.
Zeichne nicht sichtbare Kanten gestrichelt.

Verbinde zum Schluss die Eckpunkte und beschrifte die Kanten.

Übung 1

Zeichne das Schräbild eines Vierecksprismas mit einem gleichschenklige Trapez als Grundfläche und der Körperhöhe h_K = 11,6cm.

Grundfäche: a = 4cm; α = 63°; d = 2,2cm und c = 2cm;

Vergleiche dein Lösung mit dem Vorgehen im Video.

Tipps zum Zeichnen der Grundfläche:

Tipps zum Zeichnen des Schrägbildes des Prismas:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 2

Bearbeite die Aufgaben aus dem Buch. Zeichne mit einem spitzen Bleistift und einem Geodreieck. Nutze bei Bedarf die Tipps und vergleiche deine Lösungen.

• S. 148 Nr. 1
• S. 148 Nr. 2 (a oder b.)
• S. 149 Nr. 3 (Wähle drei Grundflächen aus.)
• S. 149 Nr. 4
• S. 149 Nr. 5 (Wähle zwei Prismen aus.)
• S. 149 Nr. 6

Prüfe deine Schrägbilder aus Nr. 1 mithilfe des GeoGebra-Applets. Für die drei Lagen vertausche je a und b, a und c oder b und c.

Prüfe hier deine Schrägbilder aus Nr. 3 a und b

Prüfe hier deine Schrägbilder aus Nr. 3 c, d, e, f, h und i

Ideensammlung

IDEENSAMMLUNG:

https://www.aufgabenfuchs.de/mathematik/koerper/prisma.shtml
https://de.serlo.org/mathe/1625/prisma